GSM network security: data encryption

Disclaimer This article is published for informational purposes only; the author is not responsible for the use of materials published in this article.
I also want to immediately warn you that if you expect to find a step-by-step guide to listening to GSM traffic in this article, or hope to read this article to get access to telephone conversations of your friends, acquaintances, pets , then it is better to ignore it. Here you will not find anything interesting. There is no truth, do not go under the cut, there is boredom.

Part 1: GSM Security Highlights

Before proceeding to the description of the encryption algorithm used in GSM networks, we consider how the user is authenticated and the encryption key is generated. To do this, we will use a picture borrowed from Wikipedia (I apologize for the quality, I did not find anything better).


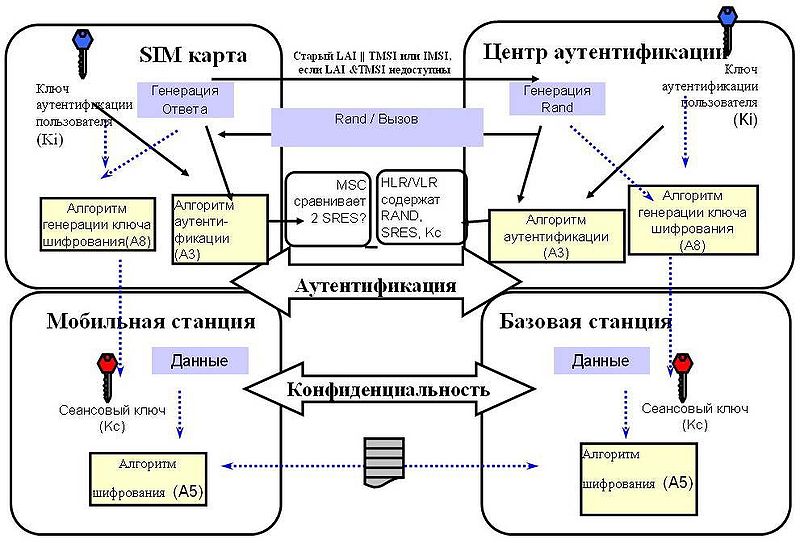
This figure shows the following steps schematically:

1. The operator’s phone connects to the network.
2. To confirm its authenticity, the phone sends a special identification code called Temporary Mobile Subscriber Identity (TMSI).
3. The Authentication Center (CA) generates a 128-bit random number RAND and sends it to the Mobile Station (MS).
4. The MS encrypts the received RAND number using its secret key K _i and the authentication algorithm A3.
5. The MC takes the first 32 bits from the sequence obtained in the previous step (let's call them SRES (signed response)) and sends them back to Central Asia.
6. Central Asia performs the same operation and receives a 32 bit XRES (expected response) sequence.
7. After that, CA compares SRES and XRES. In case both values ​​are equal, the phone is considered authenticated.
8. MS and CA calculate the session encryption key using the secret key K _i and the key generation algorithm A8 K _c = A8 _ki (RAND)

')
Speaking about the A3 authentication algorithms and the A8 key generation algorithm, it should be noted that in practice most cellular operators use one algorithm for this purpose, called COMP128 (it has many modifications COMP128-1, COMP128-2, COMP128-3).
COMP128 is an ordinary hash function, at the input that accepts a 128-bit sequence and returns 96-bit at the output.
So, instead of using different algorithms for authentication and the formation of the session key, the following scheme is used:
SRES = First 32 bits from COMP128 (K _i || RAND)
K _c = Last 64 bits of COMP128 (K _i || RAND).
As always in cryptography, the attempt to save time for developers turned into a complete failure. The security of GSM networks was initially based on the principle “security at the expense of obscurity”. And when, in 1998, the algorithm was uncovered by a group of researchers consisting of Marc Briceno, Ian Goldberg and David Wagner, one interesting feature was cut off: the last 10 bits of the secret key K _{i were} always zero. Using this curious property, as well as the COMP128 vulnerability to Marc Briceno's “birthday days attack”, Ian Goldberg and David Wagner were able to extract the secret key K _i from the SIM card.
The result of this study was the widespread rejection of the COMP128 algorithm and its replacement with more reliable modifications COMP128-2 and COMP128-3, the technical details of which are kept secret. Hmm ... does this remind you of anything?

Part 2: A5 / 1 encryption algorithm

Let's now move on from things more general to more private things and talk about how phone call encryption is implemented in GSM.
As an encryption algorithm in GSM, algorithms from the A5 family are used. Today, there are only 3 of them:

• A5 / 1 - stream cipher, the most common today.
• A5 / 2 is a variant of the previous algorithm "for the poor." It is very similar to its “elder brother”, but initially it was thought of how greatly weakened the A5 / 1 version was. Currently not used
• A5 / 3 block cipher. Developed in 2002 to replace the outdated A5 / 1. However, currently used only in 3GPP networks. A number of vulnerabilities have been found for the algorithm, but there is no talk about practical attacks yet.

Let us consider the algorithm A5 / 1.
So, as mentioned above, A5 / 1 is a stream cipher. And once again a picture from Wikipedia is in a hurry:

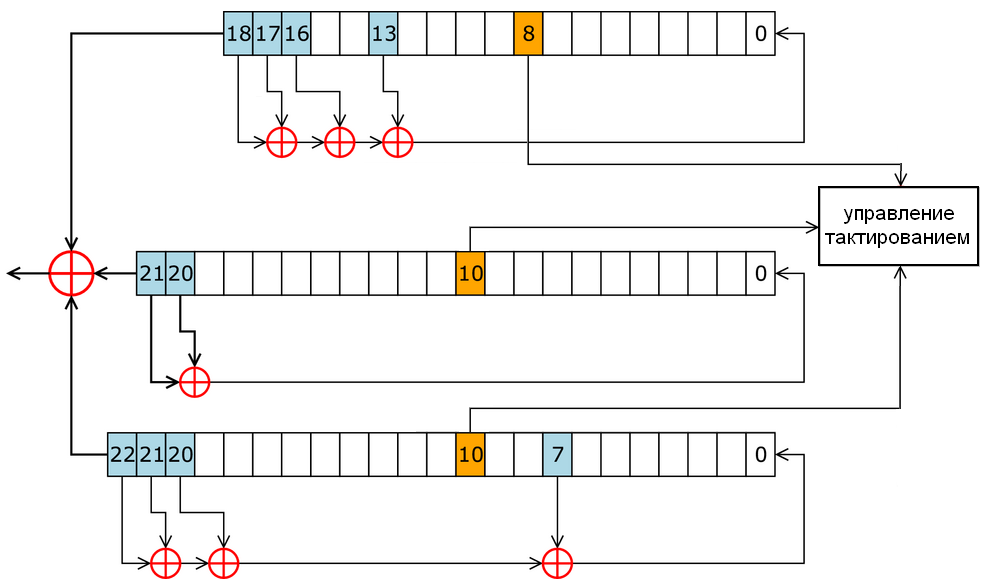
The internal state of the cipher A5 / 1 consists of three linear shift registers with feedback R1, R2, R3, 19, 22 and 23 bits in length, respectively (total 64 bits).
The shift in the registers R1, R2, R3 occurs only when a certain condition is met. Each register contains a clocking control bit. In R1 it is the 8th bit, and in R2 and R3 - the 10th. At each step, only those registers whose sync bit value is equal to most of the sync bit values ​​of all three registers are shifted.

Before the algorithm is executed, the registers are initialized. It happens as follows:

1. R1 = R2 = R3 = 0
2. For i = 0 to 63 do
   R1 [0] = R1 [0] ⊕Kc [i]
   R2 [0] = R2 [0] ⊕Kc [i]
   R2 [0] = R2 [0] ⊕Kc [i]
   Shift all registers by one position, ignoring sync bits.
3. For i = 0 to 22 do
   R1 [0] = R1 [0] ⊕ FrameCount [[i]
   R2 [0] = R2 [0] ⊕FrameCount [[i]
   R2 [0] = R2 [0] ⊕FrameCount [[i]
   Shift all registers by one position, ignoring sync bits.
4. For i = 0 to 99 do
   Shift registers by one position, taking into account the synchronization bits.

Where FrameCount 32-bit record the number of the current frame.

After initialization, 228 bits of the output sequence are calculated. 114 bits are used to encrypt data coming out of the network to the mobile phone, the remaining 114 bits are used to encrypt data from the phone to the network. Encryption itself is an ordinary XOR between the data and the key stream produced by the A5 / 1 algorithm.
After the data transfer, the frame number is incremented by one and the registers are initialized again.

We use the description above and implement A5 / 1 encryption in C #.

You can check the correctness of the code by running the program with the key {0x12, 0x23, 0x45, 0x67, 0x89, 0xAB, 0xCD, 0xEF} and the frame number 0x134. Two generated sequences of 114 bits each, should be equal, respectively {0x53, 0x4E, 0xAA, 0x58, 0x2F, 0xE8, 0x15, 0x1A, 0xB6, 0xE1, 0x85, 0x5A, 0x72, 0x8C, 0x00} and {0x24, 0xFD, 0x35 , 0xA3, 0x5D, 0x5F, 0xB6, 0x52, 0x6D, 0x32, 0xF9, 0x06, 0xDF, 0x1A, 0xC0}.
These are the test data used by Marc Briceno, Ian Goldberg and David Wagner in their very first implementation of the algorithm written in C.

The encryption / decryption function using this class will look like this:

 private byte[] A5Encyptor(byte[] msg,byte[] key) { A5Enc a5 = new A5Enc(); int[] frame = new int[1]; bool[] resbits = new bool[msg.Count]; int framesCount = msg.Length / 228; if ((msgbits.Length % 228) != 0) framesCount++; for (int i = 0; i < framesCount; i++) { frame[0] = i; a5.KeySetup(key, frame); bool[] KeyStream = a5.A5(true); for (int j = 0; j < 228; j++) { resbits[i * 228 + j] = msgbits[i * 228 + j] ^ KeyStream[j]; } } return a5.FromBoolToByte(resbits, false); } 

Now that we have a function that allows us to encrypt and decrypt data, let's talk about the vulnerabilities of the A5 / 1 algorithm.
Today, a large number of successful attacks on GSM encryption are known, and all of them belong to known-plaintext attacks, i.e. to recover the key, the attacker, in addition to the encrypted frames, also needs to know the unencrypted data that corresponds to these frames. At first glance, such a requirement may seem fantastic, but due to the specifics of the GSM standard, in which, in addition to voice traffic, various system messages are transmitted, such attacks from the theoretical level become practical. GSM system messages contain duplicate data and can be used by an attacker. In particular, the method proposed by Karsten Nohl in 2010 is based on the search for such data in a ciphertext and a simple search for various variants of keys stored in rainbow tables until a key is generated that generates the desired ciphertext for a previously known system message. .

Part 3: Attack on the A5 / 1 algorithm

However, we do not have the enormous resources needed to compute rainbow tables, so we implement a simpler attack related to the so-called "Correlation attacks".
The attack we were considering was first described in 2002 by two researchers: Patrik Ekdahl and Thomas Johansson.
From the definition of the initialization procedure, we can conclude that the initial state of the registers is a linear function of the session key K and the frame number F _n .
Knowing that the generator output bit is the XOR of the output bits of all three registers, we can write the following equation:

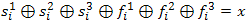( 1 )

where s _{i is the} sequence generated by registers after loading only the bits of the key K into them. f _{i is the} sequence, after loading only the bits of the frame number, and the x-output bit of the register.

We also know from the definition of initialization that the first 100 cycles of the algorithm work “idle”, i.e. produces no output bits, and the first bit of the output sequence is in fact the 101st generated bit. Thus, if we consider that at each step the probability of a shift for each register is 3/4, we can assume that after step 101, each register has shifted exactly 76 times. Therefore, formula (1) is converted to:

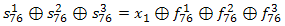( 2 )

Denoting the right part (2) as rewrite the formula:

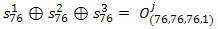( 3 )

Because the expression in the right part of (3) we know, we get 1 bit of information about the key sequence S, namely about the state of the 76th position of each register after initialization. Acting in a similar way, we can assume that at 102 position R1 remained also at position 76, and registers R2 and R3 moved to position 77, so we get information about the 77th position of the register, etc. In total, we need to open 64 bits to successfully restore the initial state.

Of course, the situation (76,76,76) arises exactly at the 101st step with an extremely low probability, and if we decided to act in this way, we would need to go through a huge number of frames, until finally one in which after 101 shifts the register scrolled to 76 positions. In order to reduce the required number of frames Ekdahl and Johansson proposed the following method.

There is no need to guess the specific position in which the registers rotate (cl ₁ , cl ₂ , cl ₃ ) times. It is enough just to know that with a high degree of probability each register will turn from 76 to 102 on the interval I = [100,140] output bits of each frame.
Thus, for each frame we can calculate the probability: as

( 4 )

Where



and denotes the probability that the tth bit was generated by register positions (cl1, cl2, cl3).

By calculating (4) for each available frame we average the probabilities obtained using the logarithm:

(five).

If (5)> 0, then s ₁ (cl1) ⊕s ₂ (cl2) s ₃ (cl3) = 0, otherwise s ₁ (cl1) s ₂ (cl2) s ₃ (cl3) = 1 .

We describe the attack completely in the form of an algorithm:

1. Select interval C. For example, C = [79.86]
2. Let the variables cl ₁ , cl ₂ , cl ₃ run through all the values ​​from interval C, for each frame we calculate (4)
3. For all obtained values, we calculate (5)
4. Based on the value of Δ, we choose the value of s ₁ (cl1) ⊕s ₂ (cl2) ⊕s ₃ (cl3)

The result of the execution of this algorithm will be 512 equations of the form s ₁ (79) ⊕s ₂ (79) ⊕s ₃ (79) = 0, consisting of 8 unknowns. Solving this system of equations by simple enumeration, we get 8 bits of the initial value of each register.
Repeating the algorithm two more times for the intervals [87, 94] and [95, 102] we get 24 bits of the initial state of each of the registers. This is more than enough for us. Scrolling each of the registers 101 times back we will get just the state of the registers that was after the second initialization step, i.e. after loading into the key bit registers. And now we can generate the entire key sequence entirely.



Using the FindKeyBit function as follows:

 private bool[] attack() { bool[] keypart=new bool[512]; int count = 0; A5attack tryattack = new A5attack(); for(int i=79; i<87;i++) for(int j=79; j<87; j++) for (int k = 79; k < 87; k++) { bool temp=tryattack.FindKeyBit(i, j, k, keystream); int time = finish - start; keypart[count] = temp; count++; } return keypart; } 

we get an array of 512 values ​​in which the XOR key bits are written from position 79 to position 86.

Having received all 24 bits from each register, and translating them into byte arrays, we check our solution:

 Private void checkSolution() { A5attack LetsAttack = new A5attack(); int[] testframe = new int[1] { 0 }; bool[][] startState = LetsAttack.checkSol(first, second, third); A5Enc a5check = new A5Enc(startState); bool[] TempFrame = new bool[228]; a5check.KeySetup(testframe); TempFrame = a5check.A5(true); for (int l = 0; l < 228; l++) { find = true; if (keystream[l] != TempFrame[l]) { find = false; break; } } } 

If the received frame coincides with the first frame of the known key stream, then the attack was implemented successfully and we opened the session key of the algorithm A5 / 1.

Part 4: Final

To summarize, I want to note that the attack described is one of the first such attacks. The most advanced of them allows you to open a session key of a total of 2000 frames with a 90% chance (9 seconds of conversation). Thus, correlation attacks are a very serious threat not only in theory, but also in practice.

Literature and links

• Marcin Olawski. "Security in the GSM network".
• Patrik Ekdahl and Thomas Johansson. "Another Attack on A5 / 1".
• Karsten Nohl. “Attacking phone privacy”.
• Marc Briceno, Ian Goldberg, and David Wagner. A pedagogical implementation of A5 / 1.

PS: the author will be grateful if someone will share the work of Barkan, Elad; Eli Biham (2005). "Conditional Estimators: An Effective Attack on A5 / 1". It describes the attack that I mentioned in the final part.
UPD: all question cleared, thanks to the user whitequark .