Game "sea battle": the placement of ships

Good day, dear! Unfortunately, due to the hospital regime, I could not publish my latest research on the subject of the game “Sea Battle” for the last month. I hope my note will be useful for someone, and even if it will be a partial repetition, it will be in a new interpretation.
So, today I would like to discuss the issue of the deployment (not optimal, but arbitrary) of the ships before the battle. On the left, you see an example of the result of the following algorithm: ships in the shape of the letters “R”, “A”, “H”, “B” are placed on the playing field of 5x15 with a few forbidden cells (marked in green). Interested please under the cat.

I note that the generation of the arrangement is relevant not only for an artificial rival, but also for a person: to create relatively equal strategic conditions, the ships of a live player must be arranged pseudo-randomly. In this article, an algorithm is considered that is guaranteed to find a valid constellation (taking this finite time, the upper estimate of which can be obtained), if it exists (respectively, it can characterize the principle possibility to arrange ships in the proposed conditions).

Number of options

If we consider a non-classical squadron, then the total number of options for deploying ships is calculated by the formula:

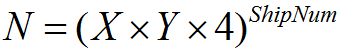
This formula takes into account all possible options: even a priori dead-end. The need for this formula is caused by the desire to number each option, and then later to check a specific number for acceptability. It is easy to see that for 10 ships and a field of 10x10, we get a number on the order of 10 ^ 26, which means that for indexation we need a variable of 87 bits in size, taking into account the alignment - a total more. Moreover, an increase in the field, or, even worse, the number of ships, aggravates the situation. So adding just one ship increases the number of options to about 10 ^ 28. No built-in (hardware-supported) data type is suitable for working with such numbers. Of course, you can emulate arithmetic with large numbers, but this will result in a loss of performance and an unnecessarily large supporting toolkit for one task of the game logic engine. In addition, the use of indexation implies a comparison of each index of a unique arrangement, that is, the index will still “decay” into a certain set of numbers characterizing the coordinates and angles of rotation of the ships. If you think about it, you can get around the problem of large numbers, using the nature of the subsequent use of the index.

Bust options for one ship

In fact, we say: a troika of numbers characterizes a ship, and a set of such "triples" - a squadron. Having ordered the characteristics, we can clarify: the first number characterizes the ordinate and varies from 0 to (Ymax-1), the second - the abscissa and belongs to [0; Xmax-1], the latter is the angle of rotation, which assumes four allowed states. A little thought, you can imagine the keys that characterize the position and rotation of the ship in the form of an Ordinate-Abscissa-Angle tree (one deck is marked to simplify perception; the working area is a 2x2 field):

A depth search on this tree will return {000}, {001}, {002}, {003}, {010}, {011}, {012} ... {{}} values. It is easy to see that the enumeration of keys resembles the enumeration of numbers of the positional number system, in which each digit has its own range of values. Since each digit of our system is independent and characterizes one of the ship’s degrees of freedom, the key generation algorithm can be represented as the following virtual machine:

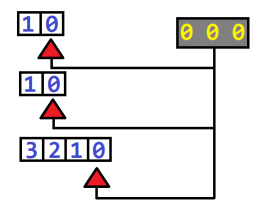
Moving the bottom rail, we will consistently get the keys: {000}, {001}, {002} and {003}, after which the rail “will end”. After exhaustion of the junior level, we return its rail to its initial state and shift the average one position. The generator returns {010}, {011}, {012} and {013} - the low and middle digits are exhausted. We “reset” the state of all exhausted bits, and shift the top rail by one position: {100}, {101}, {102} and {103}.
Thus, the algorithm for requesting the next key is as follows:

')

Enumerate squadron options

Having dealt with one ship, we can abstract a little and solve the task for the squadron. The principle of key generation is the same, but instead of rails, the generators discussed above now appear. We successively iterate over all the values ​​of the low-order bit (i.e., the low-order generator here) until it overflows, then “increment the next bit after it” (that is, request the new value from the corresponding generator) and re-scroll the low order:
{{000}, {000}}
{{000}, {001}}
{{000}, {002}}
{{000}, {003}}
{{000}, {010}}
...
{{000}, {113}}
{{001}, {000}}
...
{{113}, {113}}

Spread Generation

So, finally, we solved the first problem: we can iterate through all possible arrangements. Now consider the issue of validation options.
The algorithm is simple: we get the key for the first ship, if it is possible to place the ship, we place it on the field and proceed to the next ship, otherwise we generate the next key for this ship. If the keys are over, we give a signal “higher”: for the previous ship, we select a new valid key, reinstall the ship and “return”. Everything is exactly as with the numbers in the positional system, only a number of restrictive rules have appeared, prohibiting some combinations.
For convenience, the rules can be divided into logical categories, thus accelerating the check by introducing mandatory criteria. For example: the ship must be fully fit on the playing field. This simple criterion, in relation to the case considered above, will allow you to immediately cut off 75% of the arrangements. Further checks depend on the organization of the data in your implementation.

Accidents

All this is good, but a deterministic sequence of actions will always generate the same combination, even if there are several of them available. The solution is simply outrageous: you need to mix the numbers on the rails in the generators. Simply, reading i from the rail, return to the call point the value of the i-th element of a certain array random_num [i].
In mixing the elements of the array, we can recommend the following.
First, the formula is guaranteed to generate the index of the second element for exchange, different from the first. Of course, you can not prohibit the fictitious exchange of random_num [j] <-> random_num [j], but why spend an iteration on this?

//N –     //% -    unsigned a_indx=rand()%N; unsigned b_indx=(a_indx+1+rand()%(N-1))%N; //      //-  '%' –    //  

Secondly, the minimum sufficient amount for complete mixing ( disorder ) is expressed as

 ceil(N*0.5); 

An example of mixing numbers on the “younger” rail and a “good” generator are given below:

Two iterations of the exchange led, in this case, to complete mixing. Please note: this generator, like the original one, will return the entire set of keys, but in a different order, which will allow to create different arrangements from time to time. I note that the "randomness" concept is largely subjective, and intact slats can be considered random.

In the previous series

• The optimal algorithm of the game in the sea battle ( GORKOFF )
• The theory and practice of the game "Battleship" - to be honest ( born2fly )
• Algorithm of the “sea battle” game: shelling the enemy ( impersonalis )
• Again "sea battle". Count the number of possible ship locations ( Mrrl )

(I apologize if I forgot to mention someone; report to PM)

Conclusion

Thanks to everyone who mastered this article, highlighting their time for reading. I will try to answer your questions and comment on the criticism. Request: comments and tips on proofreading to write in a personal, so as not to divert the discussion from the subject of the article.