Geekly Articles each Day
📜 ⬆️ ⬇️

Index the sky

image
The need for spatial search arises quite often. As well as in spatial JOIN'e - finding the intersection of two sets of features. Not always want to attract heavy artillery. Well, let's try to think of a way to solve the problem with “a little blood, a mighty blow”.


Introduction

It is known that indexing of more than one-dimensional objects is a significant problem, although the need for this is quite large. The difficulties are objective. whatever we do, the index file on the physical media is sequential (one-dimensional) and we must provide some sort of traversal order of the plane (space). At the same time, there is an intuitive desire to locate points in space that are not very far in the index file. Unfortunately, without breaks it is impossible.

The relationship to spatial indexing in the GIS community is generally twofold. On the one hand, a fair number of members of this community are confident that there is no problem and, should such a need arise, they would cope with it in two accounts. On the other hand, there is an opinion that “everything is already stolen before us”, most modern DBMS somehow know how to solve this problem, some for a long time and, in general, successfully.
')
As it often happens, the fact that we do not see a gopher does not mean that it is not there. As soon as the data volumes grow significantly, it is found that the construction of the spatial index itself can be a problem, since either the algorithm goes beyond the definition, or the construction time becomes unacceptably large, or the search is ineffective ... As soon as spatial data begins to change intensively, the spatial index may begin to degrade. Index rebuilding helps, but not for long.

Here we consider the simplest case of indexing spatial data - working with point objects. We will use honest coding of coordinates using a sweeping curve. Of course, there are other methods, pixel-block indices, R-trees, quadtrees, at worst. Perhaps this is a topic for another article, but now we are describing exactly how to work with point objects with the help of a sweeping curve.
We will not argue that the proposed method is ideal, but it has at least two advantages - it is very simple and very effective. With it, literally “on the knee”, it is possible to solve quite serious tasks.

We take the star atlas and its imitation with random numbers as data. Each data set consists of a number of objects, each of which is described:


Test data

We have several data sets:
  1. 55M - This set consists of 55,368,239 objects whose coordinates are random numbers in the interval 0 ... 2 ** 27 in X and 0 ... 2 ** 26 in Y, VAL is always 0.
  2. 526M - This set consists of 526,280,881 objects whose coordinates are random numbers in the interval 0 ... 2 ** 27 for X and 0 ... 2 ** 27 for Y, VAL is always 0.
  3. USNO-SA2.0 - This is a directory of 55.368.239 stars, obtained from ftp://ftp.nofs.navy.mil .
    X-coordinate is (RA (Right Ascension) in decimal hours) * 15 * 3600 * 100
    Y - coordinate - ((DEC in decimal degrees) +90) * 3600 * 100
    VAL - some value, which, among other things, contains the brightness in the red and blue ranges.
  4. USNO-A2.0 - This is a directory of 526,280,881 stars, which can be obtained from ftp://ftp.nofs.navy.mil . For this data, only estimates are given. Values ​​for its objects are similar to USNO-SA2.0


Theory

The idea of ​​a sweeping curve is to number the discrete space. A feature is represented by a point in N-dimensional space. A point on the plane represents itself, a rectangular extent describing a flat figure is a 4-dimensional point, etc. Such a point is a fixed-length number that is fairly easy to deal with. In particular, such a number can be placed in a regular B-tree. The search query is divided into continuous segments of the sweeping curve and a subquery is executed for each segment. All points in the subquery intervals are the sought ones.

Thus, we need a curve that will visit every point of our (two-dimensional in this case) discrete space. What are the possible options?
  1. Igloo. 2-dimensional space is numbered line by line like a scan in a kinescope. For evenly distributed point objects in two-dimensional space and for small queries, this method is ideal. Its disadvantages are:
    • Effectively works on 2-dimensional space, otherwise it generates a lot of subqueries.
    • For large search extents, a large number of subqueries are generated.
    • Ineffective for clustering-prone data.

  2. Self-similar curves. The spotting curve has a fractal nature, the unit cell (for example, a 2x2 square) is numbered in a certain way, after which each sub-cell is numbered in a similar way. The most famous of such a curve is the so-called Z-order (or bit-interleaving), the nature of which follows from the name. The numbering of the plane with a resolution of 64x64 looks like:
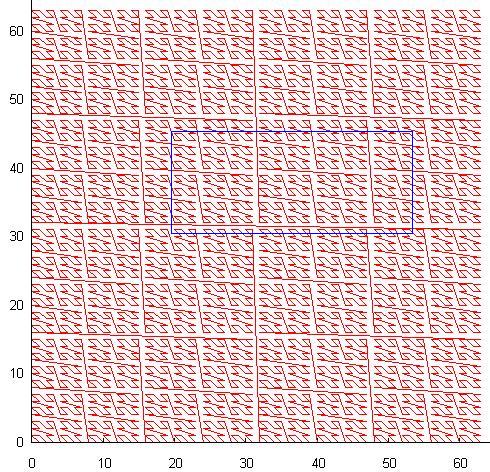
    image
    The blue rectangle in the picture is a typical search query, each time it crosses a curve, a new subquery is generated. In essence, with careless use, this method generates even more subqueries than igloo. This explains the fact that this method is practically not used in the DBMS. Although, self - similarity gives it a wonderful feature - adaptation to unevenly distributed data. In addition, continuous segments of the curve can cover large areas of space, which is useful if you are able to use it.
  3. Another version of the self-similar curve: P-shaped Hilbert curve:
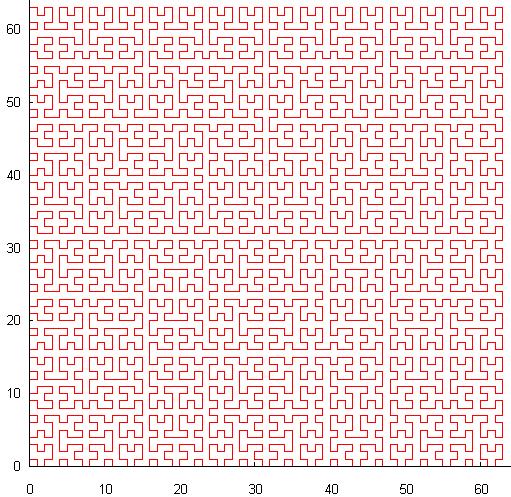
    image

    Unlike the Z-order, this curve has continuity, which allows searching a little more efficiently, a significant disadvantage is the relatively high cost of calculating coordinates from a value and vice versa.

    The third variant with self-similarity 22: The X-shaped curve intersects itself and the author does not know the precedent of its use for spatial indexing.

    Also known, the Moore curve is an analogue of the Hilbert curve, the Sierpinski curve, the Gosper curve, ...
  4. We will use the so-called. Cascade Igloo:
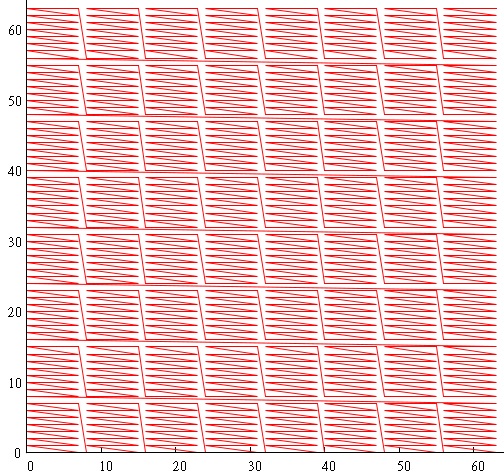
    image
    To get this picture, we divided the range of coordinates into pieces of 3 bits and mixed X & Y - i.e. the value of the sweeping curve is obtained as:
    • bits 0 through 3 are bits 0 through 3 x coordinates
    • bits 3 through 6 are bits 0 through 3 Y coordinates
    • bits 6 through 9 are bits 3 through 6 x coordinates
    • bits 9 through 12 are bits 3 through 6 of the Y coordinate
    Thus, we obtain 8X8 blocks with a line scan inside, which themselves form a line scan between themselves.
    But this is to demonstrate the principle. For indexing we will make blocks of 17 bits. If you are wondering why 17, more on that later.


results

Create index

DatasetDisk Size (Kb)Build timeMEM size (Mb)
55M211,2506'45 "40
526M1,767,152125 '85
USNO-SA2.0376,3684'38 "40
USNO-A2.03,150,000125 '85
Where:


Search index

The following tables list the values ​​characteristic of queries on the constructed index. The total values ​​for 100,000 searches for randomly selected (in a populated area, of course) square extents are given.


Spatial JOIN

The following tables list the values ​​characteristic of join'ov indexes. By join we mean the search for all objects located within a certain extent. For example, if the query parameter is 0.25 arc second, then for each element from one index a search will be performed in the second index with an extent of + - 0.25, i.e. square with sides 0.5x0.5 arc second and center at the reference point.



How and why does it work?

For a start, we note the important points:
  1. For large files, disk caching does not work, you should not rely on it.
  2. The request processing time consists mainly of disk read times, everything else is relatively short.
  3. For randomly distributed queries, no caching works, if the index is arranged as a B-tree, you should not rely on the page cache and spend extra memory on it.
  4. For spatially close requests, a small (several dozen pages) cache is sufficient.


So, let's try to understand how the data is arranged.


So how is the search done?
  1. we cut the search extent into pieces according to the block index device.
  2. each extent portion corresponds to one index block and is processed independently.
  3. inside the block we find the boundaries of the search range
  4. subtract the entire range, filtering everything that falls outside the search extent.
Even a little offensive, how simple it is.

Results

  1. Even the largest atlas of spatial objects known to us (~ 3,000,000,000 pieces) can be indexed in time, measured in hours.
  2. The amount of disk memory required to store such an index is measured in dozens (~ 30) gigabytes and is almost linear in the number of objects.
  3. The amount of RAM required for the search is very small (units of Mb), the index can be used, including in embedded systems
  4. For a spatial search along a small extent (the dimensions of which are comparable with the average distance between objects), the search time thus approaches the time of 2-3 disk operations, i.e. practically to the physical limit
  5. For relatively large queries, the search time depends more on the number of objects in the sample.
  6. In any case, the time remains predictable, which allows the use of this index, including in real-time systems


PS

The work described was carried out in 2004 in collaboration with Alexander Artyushin from the wonderful company DataEast . At that time, the author himself was an employee of this company and, yes, the publication is carried out with their consent, thanks to Evgeny Moiseyev emoiseev .
Iron in those days was not like the present, but the fundamental moments have not changed.

Source: https://habr.com/ru/post/186564/

More articles:


All Articles