Analysis of the tasks of the World Cup finals about programming ACM ICPC 2013

At the ACM ICPC 2013 World Team Programming Championship a week ago, there were 11 tasks, one of which for a given time could not be solved correctly by any of the teams.

But besides the teams, there are other people who professionally solve problems - the championship analysts. During the broadcast, they are divided into groups, distribute tasks and then talk about them in the studio. A lot of viewers are watching the air until these guys sort out the latest task. In addition, analysts tell the leader what is happening “on the field,” looking for interesting pieces of code, watching the picture from the participants' webcams.

This year, 21 analysts from Sweden, the Netherlands, the USA, Slovakia, Belarus and Russia were at ACM ICPC. And 10 of them were from Yandex. All of them in different years were ICPC winners. Especially for Habr, they dismantled all the tasks of the championship.
')

Task A. Self-Assembly

One highly scientific chemical institution is actively experimenting with the Automatic Molecule Collector. The molecules, between which the formation of chemical bonds is possible, are mixed and placed in the AFM, where they form complex molecular structures. However, sometimes a problem arises - molecules form such a large group that the Picker jams.

Write a program that will determine whether the provided set of molecules can be assembled into structures of unlimited size. In this case, 1) the task is limited to flat structures and 2) each molecule has the form of a square, all molecules have the same size. The four sides of the square denote surfaces by which molecules can combine with compatible molecules.

In each test you will be presented with a set of descriptions of molecules. Each type of molecule is described by four pairs of symbols - labels of bonds,
which means the ability of the corresponding surface of the molecule to connect with other molecules.

There are two types of link tags:

• Capital Latin letter (A..Z) and one of the symbols + or -. Two surfaces can be connected if their connection marks are marked with the same letters, but with different signs. For example, A + is compatible with A-, but not compatible with A + and B-.
• Two zero 00. Link label 00 means that this surface can not form a link (even with the same surface with a label 00).

Suppose that in the Collector there is an unlimited number of molecules of each of the described species that can be rotated and turned over. In the formation of molecular structures, molecules can be nearby only if they are compatible. Each surface of the molecule can be connected to nothing.

The figure shows an example of three types of molecules and a limited size structure assembled from them (this is not the only possible structure for given types of molecules).



Input data Input data consists of one test. Each test consists of two lines. The first line contains the number n (1 ≤ n ≤ 40000) - the number of types of molecules. The second line contains n substrings of 8 characters each - a description of each type of molecule, with the surfaces being described clockwise.

Output Output the word unbounded if the molecules can create an infinite structure and the word bounded otherwise.

Problem Solving A
The author of the analysis is Vasily Astakhov, ACM ICPC 2011 bronze medalist in the team of Moscow State University. Mv Lomonosov.

The task requires to understand whether there is an unlimited molecular structure in which the molecules have the form of squares with different bonds on the sides. Given the availability of rotation and reflection operations, to solve the problem, it was necessary and sufficient to understand whether a cycle of molecules exists. Then, for example, shifting all the time to the right and down, one would get an unbounded structure on the plane, while no connections, except those adjacent to the cycle, would be involved in the molecule. To find the cycle, it would be possible to construct a graph in which the vertices are types of compounds, and edges from the type of compound X [+/−] go to all types of compounds Y , for which there exists a molecule containing both Y and X [- / +] (double top). Then, finding a cycle in such a graph, we obtain the existence of a cycle in the original one. The task of finding a cycle in a directed graph on 52 vertices ( A +, A -, ..., Z +, Z -) is simple and can be solved, for example, by constructing strong connectivity components (the existence of a component larger than one vertex will mean a cycle).

Problem B. Hey, Better Bettor

The recent recession hurt entertainment facilities, including the gambling business. There is fierce competition among casinos, and, in order to attract players, some of them began to hold particularly attractive promotions. Casino promotions include the following: you can play as much as you want. And after you finish, whatever amount you lose from the moment you start, the casino returns x% of your losses. Naturally, if you are the winner, you take it all.

In this case, there are no restrictions on the duration of the game, nor on the amount of money with which you come into the game, but you can use this action only once.

For simplicity, we assume that all bets are worth $ 1, and the gain is $ 2. Now suppose x is equal to 20. If you make only 10 bets before you finish the game, and only 3 of them win, then your total loss will be 3.2 dollars. If 6 bets win, your winnings will be $ 2.

Given x and p (the probability of winning a single bet as a percentage), you need to write a program to determine the maximum expected gain that you can receive using any strategy of the game.

Input data The input data consists of one test that contains the return percentage x (0 ≤ x <100) and the probability of winning in percents p (0 ≤ p ≤ 50). x and p are no more than two digits after the decimal point.

Output Print the maximum expected gain with an absolute error of no more than 10 ^-3 .

Solution of Problem B
The author of the analysis is Mikhail Levin , bronze medalist of ACM ICPC 2007, silver medalist of ACM ICPC 2008 as part of the team of Moscow State University. Mv Lomonosov.

Note that the decision to stop the game now depends only on the current gain or loss of the player - the story does not matter. It can be shown that the optimal strategy in this case always has the form “stop, if you have winnings A or lose B ”, where A and B are some non-negative integers. With fixed A and B, in order to calculate the expected profit, you need to be able to solve this problem: to find the probability P ( A , B ) that the player at some point reaches win A , while never before having a loss B or more. If this problem is solved, the expected profit of the strategy is calculated as where x % is the discount provided by the casino to the player in case of loss.

For the numbers P ( A , B ), the recurrence relation holds:

,

where p is the probability of winning each time a coin is thrown. Moreover, P (0, A + B ) = 1, and P ( A + B , 0) = 0. If we solve this linear recurrent of order 2, we get

,

Where .

If we could go through all the possible pairs ( A , B ) for each input ( x , p ), then we would do it, and then choose the best one. Par ( A , B ) is an infinite number, but if you conduct several numerical experiments, you can see that as A and B increase, the expected profit first increases, and then begins to fall (you can prove the convexity of the expected profit as a function of A and B ), therefore always enough to check only a finite number of pairs. In addition, it can be noted that the best values ​​for A and B are the larger, the closer p is to 0.5, and x - to 100. The worst possible case is p = 0.4999, x = 99.99. It turns out that in this case it is enough to go through A up to 21000, and B - up to 2500, and such a search is enough for the solution to pass through time limits.

Problem C. Surely You Congest

You are responsible for the intelligent traffic management system for new cars. Your goal is to avoid traffic jams from drivers commuting from the sleeping areas to the city center during the morning rush hour, using information about the city and the movement of other cars.

Unfortunately, due to the fact that drivers are selfish, they will never follow the shortest possible way to the center, even if you ask them about it. You can only advise them which of the few shortest paths to choose.

The city consists of intersections connected by two-way roads that can be reached in a given time. All drivers begin their movement at intersections (possibly different) and end at the same intersection number 1 designated as the city center. If two drivers simultaneously start driving along the same road in the same direction, a traffic jam will arise and your goal will fail. However, drivers can drive through the same intersection at the same time or drive along the same road, driving in at different times.

Determine the maximum number of drivers who can get to the city center without traffic jams, if all drivers start their movement at the same time and none of them will go the non-optimal way.



In the picture, the cars are shown in their initial position. One driver is already in the center, and of the cars at the 4th intersection, one can move along the dotted line through intersection 3, the other along the dotted line through intersection 2, but the remaining two cannot reach the center without traffic jams. Thus, the answer to this test will be 3.

Input data The input contains one test. The first line contains three numbers n, m and c , where n (1≤ n ≤ 25000) is the number of intersections, m (0 ≤ m ≤ 50,000) is the number of roads in the city and c (0 ≤ c ≤ 1000) is the number of drivers. Each of the following m lines contains three numbers x _i , y _i and t _i describing the road, where x _i and y _i (1≤ x _i , y _i ≤ n) are the numbers of the different intersections that are connected by the described road and t _i ( 1≤ t _i ≤ 10000) - the time that the driver must spend to get from the beginning to the end of the road in any direction. It is guaranteed that you can reach the center from any intersection. The last line contains c numbers describing the initial intersections where cars are located.

Output Print the maximum number of drivers who can reach the city center without traffic jams.

Solution of Problem C
The author of the analysis is Mikhail Levin.

We calculate the shortest distances d ( u ) from all vertices u to the final vertex e with the help of the Dijkstra algorithm with a bunch of O ( m log n ). Since everyone wants to go only along the shortest path, cars will only travel along such edges ( u , v ) in the direction from u to v , that d ( u ) = d ( v ) + l ( u , v ), where l ( u , v ) is the length of the edge ( u , v ). We construct a new directed graph consisting only of such edges.

For any two machines that began to move simultaneously and moving from their starting points to the ending point with the same speed, the difference in distances to the final vertex remains always constant. Therefore, two cars, starting at different distances, can never drive along the same edge at the same time. Group all machines by distance from the end point. Then for each group it is necessary to find the largest number of pairwise disjoint path edges from all starting vertices to the final vertex in the new oriented graph. This problem is solved using the algorithm for finding the maximum flow in the graph: add a source to the graph and draw edges from it to all vertices, in which there are machines with a capacity equal to the number of machines at the top. We make all the edges of the oriented graph throughput 1. If we find in this graph the maximum flow from the source to the final vertex, then we’ll get the maximum number of pairwise non-intersecting paths along the edges.

Let us find the maximum flow for each group of vertices at one distance from the final one and add the answers - this will be the answer to the problem. It takes O ( m ) to find one increasing flow path, and in total such paths will be found not more than c , therefore, in total, all starts to find the maximum flow will be performed in no more than O ( mc ). Total complexity of the solution is O ( m log n + mc ), which goes into the given constraints.

Task D. Factors

One of the fundamental theorems of arithmetic says that any number greater than 1 can be uniquely represented as a product of primes. However, this unique set of prime factors can be ordered in various ways. For example:



Let f (k) denote the number of different ways to order the prime factors of the number k . Then f (20) = 3 and f (10) = 2.

You are given a positive integer n , and it is guaranteed that for any n there exists k such that f (k) = n . Determine such minimum k .

Input data The input file contains no more than 1000 tests, each of which is written in a separate line. Each test consists of a positive integer n <2 ⁶³ .

Output For each test, output the number n and the minimum k > 1 such that f ( k ) = n . The numbers in the tests are chosen in such a way that k <2 ⁶³ .

Solution of Problem D
The author of the analysis is Renat Gimadeev , ACM ICPC 2012 gold medalist in the Fiztekh team.

This is a content simple task that has many different solutions. I will give one of the shortest.

Note that if we decompose into simple factors n = p ₁ ^{k ₁} p ₂ ^{k ₂} ... p _t ^{k _t} , then the number of ordered representations in the form of a product of simple will be equal to . This follows from simple combinatorial arguments: you can order N different prime factors N! in ways. If among these factors there are identical, then all orderings, which differ only in the order of identical factors, actually coincide. Each group of k _i identical factors can be rearranged k _i ! in ways. Therefore, each unique permutation was counted k ₁ ! K ₂ ! ... k _t ! times and this number must be divided. This formula allows us to quickly calculate f ( k ), knowing the decomposition of the number k into prime factors.

Further, it should be noted that the number of orderings does not depend on what is equal to p _i and how k _i are ordered among themselves. Therefore, if we are looking for the minimum number, then we should look for it among the numbers of the form n = 2 ^{k ₁} 3 ^{k ₂} 5 ^{k ₃} ..., and k ₁ ≥k ₂ ≥k ₃ ≥ ... It turns out that such numbers among the numbers less than 2 ⁶³ not so much (in the condition they are asked to search for only those solutions that are less than 2 ⁶³ ), there are about 40,000 of them and they are easily generated by recursion. For each of them, you can find f (k) using the formula described above and store in the associative array the minimum values ​​of the number k for each obtained f (k ). After that, each request from the condition is processed during the access to this associative array.

Task E. Harvard

The term “Harvard Architecture” applies to a computer with physically shared memory for instructions and data. The term comes from the name of the computer Harvard Mark I , created in 1944. It used paper tape for instructions, and a relay for data.

Some modern microcontrollers use "Harvard architecture", but not paper tapes and relays! The data is in banks, each of which contains the same number of cells. Each data access instruction has a byte-offset f within the bank and a bit a , which is used to determine the bank number. If a is 0, then the call is made to the bank with number 0. If a is equal to 1, then the bank number is stored in the special bank selection register (RMB).

For example, suppose we have 4 banks with 8 cells each. You can access cell number 5 in one of two ways: one instruction with a = 0 and f = 5 or two instructions, setting the value of the RVB to 0 and then using the instruction with a = 1 and f = 5 . Obviously, the first method is faster, because you do not need to assign a value to the RVB. Now suppose we need to access cell 20 in the same memory. Now we can apply only one way: execute the instruction, setting the value of the RTD 2 (if the desired value is not already stored in it), and then the instruction with a = 1 and f = 4. The program is a sequence of operations. Each operation is:

• variable reference is written as Vi , where i is a positive integer;
• repetition is written as Rn E , where n is a positive integer, and — , n .
  
  The task is to determine the minimum program execution time. Namely, knowing the number and size of banks, as well as having a program, it is required to determine the minimum number of instructions 1 (accessing the cells and, possibly, setting the value of RTDs) necessary to run the program. To do this, you need to associate variables with memory cells and, among all the mappings, determine the one that minimizes the number of instructions. It is necessary to give this number itself. Please note that the value of the RVB is not defined before the first assignment.
  
  Input data They contain one test consisting of two lines. In the first b and s - the number and number of variables that can be stored in the bank. The second line contains a non-empty program with no more than 1000 elements (each of Rn , V i and E is counted as one element).
  
  It can be assumed that:
  
  • in repetition Rn , n satisfies 1≤ n ≤ 10 ⁶ ;
  • the body of repetition Rn E ;
Vi , i 1 ≤ i ≤ min ( bs; 13 );
10 12 .
Rn E ;
Vi , i 1 ≤ i ≤ min ( bs; 13 );
10 12 .

    Output Print one number - the minimum number of instructions required to run the program.
    
    Solving Problem E
    The author of the analysis is Stanislav Pak , a gold medalist of ACM ICPC 2009 as part of a team of Saratov State University.
    
    

    You can make the observation that there are quite a few interesting mappings of a set of variables on the cells of the data banks to sort them all out. Namely (the cells involved in the display will be called filled, similarly to banks, if all their cells are filled):
    
    

    1. We can assume that the zero bank is full, if there is another bank with a filled cell, because access to the zero bank is free.
    2. Banks with numbers greater than zero are identical, so we can assume that the minimum numbers of variables displayed in the cells of these banks are ordered, for example, in ascending order.
    3. We can assume that the total number of filled cells in any two banks is greater than s .

    
    
    Taking into account the cutoffs 1 - 3 and the limitations of the input data of interesting maps about 3 · 10 ⁶ .
    
    Since recourse to a zero bank is free, you can remove variables displayed on this bank from the program. For each pair of remaining variables i and j, we can predict C _ij - the cost of the operation of accessing the variable j after accessing the variable i , and then it remains to simulate the program's work.

    
    
    

    Problem F. Low Power

    
    You design advanced chips for computers. Chip production is simple and on rails, but the power sources cause a problem, since the available batteries have different output powers.
    
    Imagine that we have n machines with two chips each, and each chip is powered by k batteries. Surprisingly, it does not matter how much energy the chips consume, but it is important that the output powers of the chips differ as little as possible from each other, as in this case the machine works best. The output power of a chip is the minimum output power among all k batteries in a chip. You have 2nk batteries that you need to distribute on the chips of the machines. It may be that there is no way to distribute the batteries so that the output powers of the chips are equal for all the machines. However, you need to minimize the power difference. In more detail, you want to guarantee your customers that the difference in output power of the chips in all the machines does not exceed d , while trying to minimize d . To do this, you need to find the optimal battery distribution among the chips.
    
    Input data Consist of one test containing two lines. The first line contains two numbers n and k ( 2nk ≤ 10 ⁶ ), the second line contains 2nk integers p _i (1 ≤ p _i ≤ 10 ⁹ ).
    
    Output Output the minimum d such that there is a distribution of batteries among the chips so that the difference in output power of the chips in each machine does not exceed d .
    
    Solution of Problem F
    The author of the analysis is Stanislav Pak.
    
    

    This task is one of the easiest. It is necessary to choose from 2 nk n pairs (let's call them representatives) of the batteries, each of which
    It has a minimum power on its chip, so that the maximum difference in output power of the batteries in a pair is minimal. Suppose that d is fixed, then you can find out whether there are representatives such that the maximum does not exceed d . We sort the powers p ₁ ≤ p ₂ ... ≤ p _2nk and we will greedily type pairs: the first pair will get the batteries p ₁ and p ₂ . If p ₂ - p ₁ > d , then representatives cannot be selected. In the second pair, we take batteries ( p _i2 , p _{i2 + 1} ) with a difference of no more than d and a minimum index i 2 ≤ 2 k + 1, if possible. Similarly, in the third pair - ( p _i3 , p _{i3 + 1} ), i3 ≤ 4k + 1.
    
    If using this algorithm fails to dial n pairs, then this cannot be done. The answer will find a binary search.

    
    
    

    Task G. Map Tiles.

    
    This is a task that in the allotted time none of the teams could solve correctly.
    
    Printing maps is a difficult task. First you need to find a suitable transformation to fit the spherical earth map on the plane, then it turns out that you need to use several sheets of paper to print high-quality maps, because they do not fit onto one. To overcome this difficulty, map publishers split the map into several rectangular parts and print each part separately. It is in this process that you will take part in this task.
    
    The International Association of Card Publishers is trying to reduce the cost of printing cards by minimizing the number of individual sheets used to print cards. Even with a standard sheet size and map scale, sheet consumption can be optimized by adjusting their position.
    
    The left side of the figure shows 14 sheets covering the area. The right side shows how the same area can be covered with a total of 10 sheets, without changing the orientation of the area, the size of the sheets and scale.
    
    
    Two different ways to break down Texas sheets
    
    Your task is to help the International Association of Card Publishers to find the minimum number of sheets needed to cover a given area. For simplicity, the domain is a closed polygon with no self-intersections.
    
    Note that all sheets must be parts of a continuous grid, with sides parallel to the horizontal and vertical. Sheets can only touch their sides completely and cannot be rotated. In addition, although all given coordinates are integer, the sheets can be located in non-integer coordinates.
    
    The polygon may touch the sides of the sheets (as in example 2). However, in order to avoid problems with the machine representation of rational numbers, we can assume that the answer will not change if the vertex of the polygon is located in front of the sheet at a distance of 10 ^-6 .
    
    Input data The input consists of one test. The first line of the test contains three numbers n , x _s and y _s . The number of vertices of the polygon n (3 ≤ n ≤ 50), x _s and y _s (1 ≤ x _s , y _s ≤ 100) are the sizes of the sheets with which to cover the card. Each of the next n lines contains two integers x and y (0 ≤ x ≤ 10 x _s , 0 ≤ y ≤ 10 y _s ), describing the vertex of the polygon (in the circumferential direction either clockwise or counterclockwise).
    
    Output Print the minimum number of sheets needed to cover the polygon.
    
    Solving Problem G
    The author of the analysis is Jacob Dlugach , ACM ICPC 2012 gold medalist in the Fiztekh team.
    
    

    The solution to this problem is divided into two parts: the generation of options for the location of the polygon and counting the number of occupied cells for each of the options for the location.
    
    

    Variations generation

    
    Note that if we have found some solution, then it can be “moved” until the polygon rests on the grid (that is, further movement can change the set of selected cells). In fact, there are several cases when a polygon rests on a grid:
    
    

    • one of the vertices of the polygon falls on the grid line;
    • one of the edges of the polygon stumbles onto a grid node.

    
    
    When one of these conditions is met, a polygon still has some degree of freedom:
    
    

    • if the vertex hits the grid line, you can move the polygon along this line;
    • in the case of an edge hitting the grid node, you can move the polygon along the edge.

    
    
    We will make a reservation in advance that shifts that differ in each of the coordinates by a number that is a multiple of the grid step will be considered equal.
    
    Therefore, in fact, there are three options for selecting the “stop” so that the position of the polygon relative to the grid is uniquely defined.
    
    

    1. One of the vertices falls on the vertical line of the grid, and one of the vertices falls on the horizontal line of the grid. This includes the case when one vertex falls into a grid node. That is, the emphasis is uniquely defined by a pair of vertices, total options - n ² .
    2. One of the vertices falls on a horizontal or vertical grid line. Without loss of generality, we assume that this grid line is vertical and is given by the equation x = 0.
       Now suppose that one of the edges, which is not vertical, falls on a node. To select the shift, it is enough to choose the abscissa of this node, and this can be done in no more than m + 1 ways. For m is the number 10. Total options - n ² ( m + 1).
    3. Two non-parallel edges abut the mesh node. Here, in order to determine the shift of the polygon, in addition to the edges, it is necessary to fix the “difference” between those grid nodes against which these edges rest. Total - n ² ( m + 1) ² options.

    
    
    As a result, in the worst case, we obtain O ( n ² m ² ) polygon shift selection options. Since for each of the options, then you will need to count the number of occupied cells, you need to generate a list of all the options, clear duplicates from it: they say that it helped to reduce the number of options in the "maximum" tests by 3-5 times.
    
    It is worth noting that many teams forgot to consider some of these three cases (most of the teams stopped only before the first one).
    
    

    Calculation of occupied cells

    
    The second difficulty in this task was to effectively calculate the number of cells occupied by a given shift. The naive method of counting - for ( m + 1) ² cells, check for the presence of an intersection with a polygon - works in O ( m ² n ) and does not fit into the time limit. It turns out that it will be more efficient to count the number of occupied cells in each of the m + 1 columns. To do this, consider continuous pieces of the polygon border passing through the column: either a piece of the border “crosses” the column (one end of the piece is on the right edge of the column,
    and the other end is on the left), or both ends of the piece are on the same border of the column. It is possible to prove that the pieces of the first type are divided into pairs, and all the cells between these pieces will be occupied. After that, the resulting cells need to add cells, through which the pieces of the second type pass. This method can be implemented for O ( m ( m + n )) = O ( mn ).
    
    The total complexity of the algorithm for this problem is O ( n ³ m ³ ).

    
    
    

    Task H. Matryoshka

    
    Matryoshka called a set of traditional Russian wooden dolls of decreasing size, placed inside each other. The nested doll can be opened to get from within a smaller nested doll, which, in turn, also has a nested doll inside and so on.
    
    The National Matryoshechny Museum recently held an exhibition of dolls, which presented similar in style, but differing in the number of dolls in the doll's set. Unfortunately, one playful (and left unattended) child disassembled all the dolls and put all the dolls in a row.
    
    In the series there were n matryoshkas, each is known for its integer size. You need to re-collect all the dolls in the sets, but you do not know the initial number of sets or the number of dolls in each of the sets. You only know that each set consists of dolls of all consecutive sizes from 1 to some m , and m can be different for different sets.
    
    When assembling sets, you should follow the following rules:
    
    • you can put the nested doll only inside the larger nested doll;
    • you can combine two nesting dolls only if they stand side by side in a row;
    • after the nested doll is placed inside the set of nested dolls, it cannot be moved to another group of nested dolls or separated from the group of nested dolls. It is only allowed to temporarily divide it when combining two groups of nesting dolls.
    
    Your time is very valuable, so you want to collect all the dolls in groups as quickly as possible. The only part of the process that takes time is opening and then closing the doll, so you want to minimize the number of such actions. For example, the minimum number of actions for combining groups [1,2,6] and [4] is two; first, you need to open the nesting dolls of sizes 6 and 4. Combining groups [1,2,5] and [3,4] requires three discoveries.
    
    Write a program that calculates the minimum number of discoveries needed to assemble all sets of nesting dolls.
    
    Input data You are given one test consisting of two lines. The first line contains one number n (1 ≤ n ≤ 500) - the number of individual dolls in the original row. The second line contains n numbers describing the size of each doll in the row. The size of each doll is at least 1 and does not exceed 500.
    
    Output Output the minimum number of nesting dolls necessary to collect all the sets. If the assembly is impossible (the child could pick up several dolls himself), output the word impossible.
    
    Solution of Problem H
    The author of the analysis is Alexey Ropan , bronze medalist of ACM ICPC 2012 as part of the team of the Belarusian State University of Informatics and Radioelectronics.
    
    

    Let's say that the value of F _i is the minimum number of matryoshka openings that must be done in order to break the first i matryoshka into groups. Then F ₀ = 0 and F _i = min _{0≤j <i} F _j + G _{j + 1, i} , where the value of G _{l , r} is the minimum number of discoveries that must be made to fold the matryoshka from l to r inclusive in one (numbering of matryoshkas from one), and on the interval from j + 1 to i inclusive, all sizes of matryoshkas are different and do not exceed i - j . Then the answer to the problem will be F _n , and the complexity of the solution without taking into account the calculation of the values ​​of G will be O ( n ² ). For G _{i , i, the} value is always 0, and for G _{i , j} and i <j, at the last stage, the two groups of matryoshkas are combined. Let k be the number of the matryoshka on which the left group ends. Then G _{i , j} = min _{i ≤ k <j} G _{i , k} + G _{k + 1, j} + C _{i , k , j} , where C _{i , k , j} is the minimum number of matryoshka openings that will be required for in order to unite the groups of matryoshkas from the i- th to the k- th and c k + 1-th to the j- th. Let the value of M _{i , j} be the minimum size of the matryoshka on the interval from i to j and the value of K _{i , j , s} be the number of matryoshka on the interval from i to j , whose dimensions are less than s . Then C _{i , k , j} can be calculated as j - i + 1 - t , where t is the number of nested dolls that will not be opened when combined, that is, t = K _{k + 1, j, M i, j} + K _{i , j , M k +1, j} (you can see that one of the items will always be zero). The complexity of calculating K and G is equal to .

    
    
    

    Problem I. Pirate Chest

    
    Pirate Jack is tired of the battles, looting, theft and oppression of all and all in the open sea. He decided to retire, and even found the perfect uninhabited island in the ocean, on which he would spend the rest of his life with dignity, if, of course, he did not run out of money. Now he has a lot of gold coins, which he wants to put in the chest (he's in the end a pirate!). Jack can build a chest in the form of a rectangular parallelepiped with integer sides and not exceeding a given size of the bottom of the chest. It remains only to find where to hide the treasure chest.
    
    Jack decided to flood the chest in a shady pond. The surface of the pond is a rectangle with given sides, the pond is surrounded on all sides by vertical stone banks. Jack investigated the bottom of the pond and knows about each square of a 1x1 pond (in Cartesian coordinate system) the depth of the pond in this place. When Jack drowns the chest, the latter will sink to the maximum possible depth until it touches the bottom with at least one square. Because of the recessed chest, the water level in the pond will rise. The banks of the pond are high enough that the water never spilled over its borders. Of course, since the chest must be hidden, it must be completely below the water level in the pond. Your task is to find the maximum volume of the chest that can be hidden in the pond.
    
    The figure on the left shows a pond without a chest, in the center - a pond in which there is a chest of volume 3, on the right - a chest of volume 4 (maximum possible) in the pond. Please note that if the chest from the central pattern were placed on a unit of greater height, then its top would be visible exactly on the surface of the pond.
    
    
    
    Input data The input contains one test. The test starts with a line containing four integers a , b , m , n (1≤ a, b, m, n ≤ 500). The dimensions of the pond surface are m x n , the maximum size of the bottom of the chest is a x b . In addition, a and b is enough, the chest will never cover the entire pond completely. Each of the remaining m entry lines contains n numbers d _ij describing the depth of the pond in the square with coordinates (i, j) , where 0≤ d _ij ≤ 10 ⁹ for any 1≤ i ≤ m , 1≤ j ≤ n .
    
    Output Output the maximum volume of the chest with integer sides, which can be hidden in the pond under the surface of the water, and one of the measurements of the bottom should not exceed a , and the other should not exceed b . If no chest can be hidden under water, output 0.
    
    Problem Solving I
    The author of the analysis is Vasily Astakhov.
    
    

    , h · w , d , , S — . , h · w, , d . . ( ( a,b )) , .
    
    . , x ₀ x ₁ ( x ₀ < x ₁ , x ₁ - x ₀ ≤ b ) . , , x ₀ x ₁ . ( n ³ ). , w = x ₁ - x ₀ ≤ a , yb , y a . : ( h ), . . y . , , .
    
    ( ), . , ≥ . , . , O( n ² · m · log m ), log .

    
    
    

    J. Pollution Solution

    
    , , ( , ) , . — , , .
    
    
    
    , , . ( ) x , (0, 0).
    , . , , - .
    
    . . , n r , 3 ≤ n ≤ 100 — , 1 ≤ r ≤ 1000 — . n , x _i y _i — , −1500 ≤ x _i ≤ 1500 0 ≤ y _i ≤ 1500. . .
    
    . , r . 10 ⁻³ .
    
    J
    — , ACM ICPC 2012 .
    
    

    : , .
    
    ( , ). O — , n P ₁ , P ₂ , …, P _n , n - ( x _i , y _i ). , P _{n +1} = P ₁ .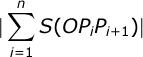
    
    ,
    
    S ( O P _i P _{i +1} ) — O , P _i P _{i +1} :
    
    .
    
    , :
    
    
    
    n , «» , , , ( ).
    
    
    
    . , , , . : O P _i P _{i +1} , , .
    
    
    
    ? P _i P _{i +1} . .
    
    

    • t P _i + (1 − t ) P _{i +1} t [0, 1] ( ). t , .
    • .

    
    
    , ( P ₁ P ₂ P ₃ P ₄ ), ( P ₅ P ₁ ) ( P ₂ P ₃ P ₄ P ₅ ).
    
    O P _i P _{i +1} (, O P ₅ P ₁ ). ( ), , . .
    
    , .

    
    
    

    K. Up a Tree

    
    — . . . , post, pre in pre- output, , output . , .
    
    .
    

     void prePrint(TNode t) { output(t.value); if (t.left != null) prePrint(t.left); if (t.right != null) prePrint(t.right); } void inPrint(TNode t) { if (t.left != null) prePrint(t.left); output(t.value); if (t.right != null) prePrint(t.right); } void postPrint(TNode t) { if (t.left != null) prePrint(t.left); if (t.right != null) prePrint(t.right); output(t.value); } 

    
    
    — ! , , , . , , .
    
    . , , . , , , . :
    
    
    • , , inPrint ;
    • 6 inPrint, prePrint postPrint, , .
    
    , . . , .
    
    . , — prePrint, inPrint postPrint. n (4 ≤ n ≤ 26), .
    
    . 6 {Pre, In, Post} — prePrint , inPrint , , postPrint. , prePrint, inPrint, postPrint , , prePrint , , , inPrint .
    
    K
    — , ACM ICPC 2007 . Mv .
    
    

    . 90. . . S ( f ₁ , f ₂ , f ₃ , s ₁ , s ₂ , s ₃ , l ) — , , f _i , i - , s _i l , — , — .
    
    , O( n ² ).
    
    3 ³ n ⁴ , , 3 ³ n ² , n ≤ 26 .
    
    

    
    
    , ACM ICPC 2013, . , , Per Austrin ( ). , ICPC. .