Honey Bees as a promising branch of computer technology development
Hi, Habr.
Recently I wondered why the binary code is being used now.
I imagined alternative reality and alternative technologies, and a very interesting concept came into my head, which I hasten to share.
Introduction:
Today we use a binary code - it is simple and reliable, but still BINARY, that is, there are only two positions “0” and “1” for encoding information.
This can be compared to a car:
- like the binary code, it was invented in the twentieth century,
- like the binary code, it rapidly developed from the right engine to the gas engine, which can be compared with the lamp and transistor systems of the elementary basis of a digital computer.
- Indeed, the car is an effective and convenient means of transportation - as well as the binary code is an effective and convenient basis for digital computing.
')
BUT it's just a car! But there is a much more complicated technique, such as helicopters and airplanes, for example.
And I am convinced that just as we mastered the sky, we will master other models of digital coding of information.
As always, the idea for the concept was presented by mother nature. Today I want to introduce you to the honeycomb technology.
Structural units:
So, for simplicity, I will give examples on a schematic lamp model.
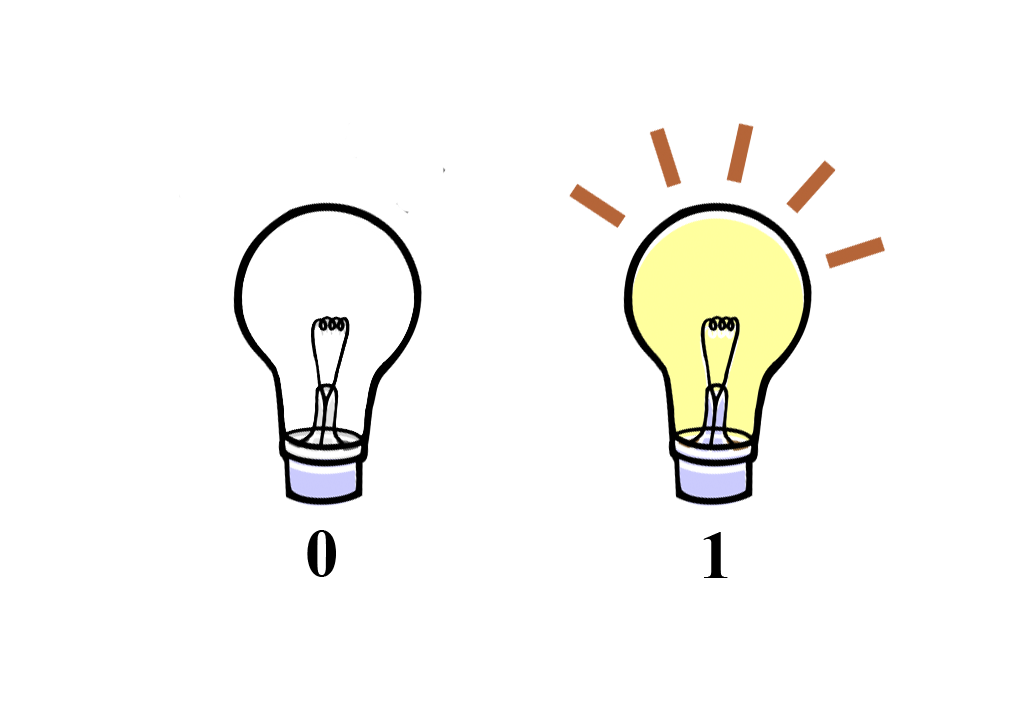
As I said in the binary system, there are only two positions - “0” and “1”. We have one light bulb that can be lit or turned off - there is no third. A light off is “0”, and an on light is “1.”
But what if we consider a hexagon model?
Instead of a light bulb, I imagine an element in the form of a hexagon, each of the walls of which has its own conductivity. In the center of the figure is the input contact (source), each face has an output contact that is connected to a common drain, and since the faces have different conductivities, the output voltage on the drain will be different (depending on which face the charge went through).
The most interesting element of the model is the bridge. Rotating in a circle, the bridge alternately connects the center of the figure with its faces.
But this is not all, each face has its own transmitting ability of a strict range, therefore the contact will be broken as soon as the voltage exceeds the permissible limit, and the bridge immediately goes to the next edge with a higher selected transmitting range.

In chips based on TTL, “zero” is expressed by a voltage in the range from +0 to +0.8 volts, and “one” - in the range from +2.4 to +5.0 V.
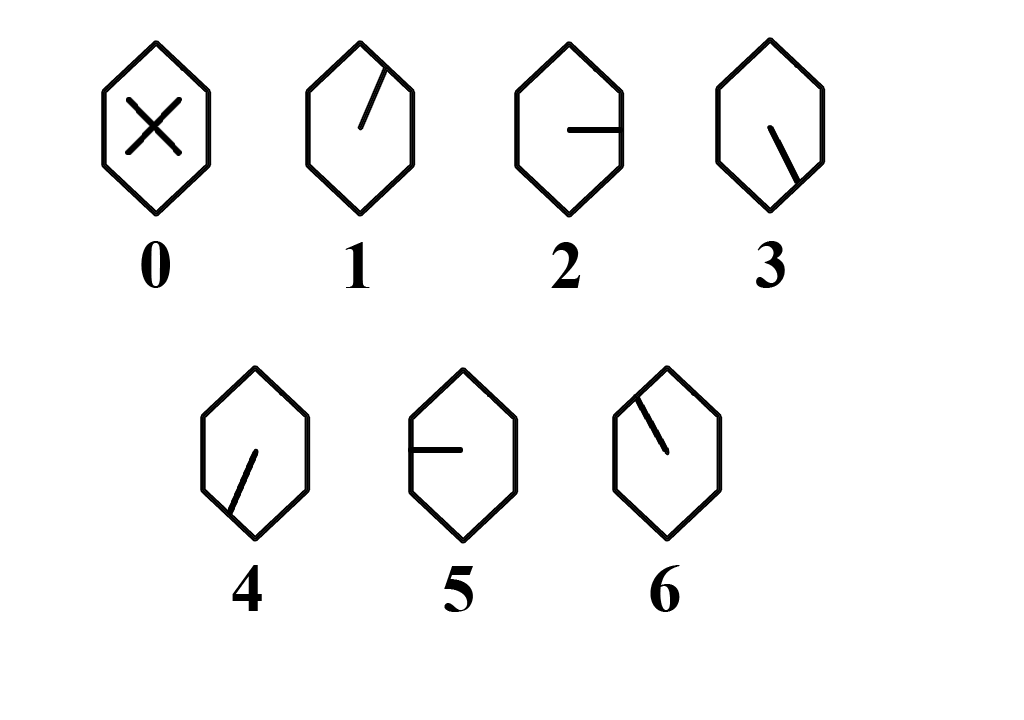
The same logic can be applied to my six-sided "bee" cell:
0 - voltage range from +0 to +0.8 Volts;
1 - voltage range from +1.2 to +2.0 volts;
2 - voltage range from +2.4 to +3.2 Volts;
3 - voltage range from +3.6 to +4.4 volts;
4 - voltage range from +4.8 to +5.6 Volts;
5 - voltage range from +6.0 to +6.8 Volts;
6 - voltage range from +7.2 to +8.0 Volts;
As we can see, each of the positions of the bridge has a range of 0.8 Volts. The range in o, 4 volts after each face, is needed to protect the system from spontaneous transitions of the bridge from one face to another.
Comparison of information capacity:
Let us now compare how effective the system proposed by me in comparison with the original one.
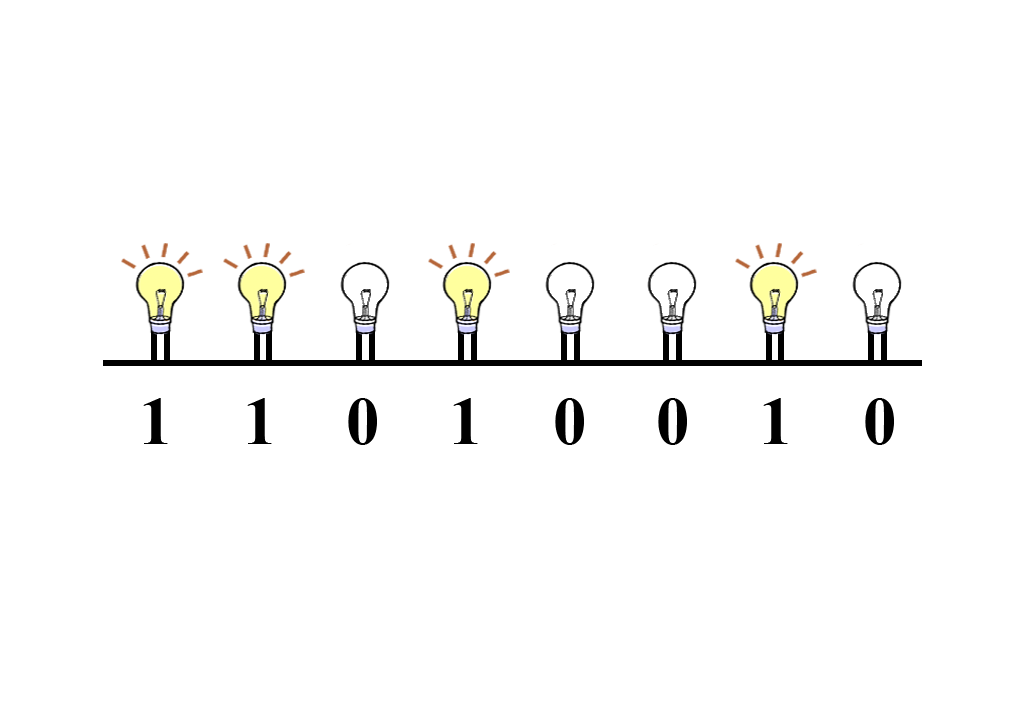
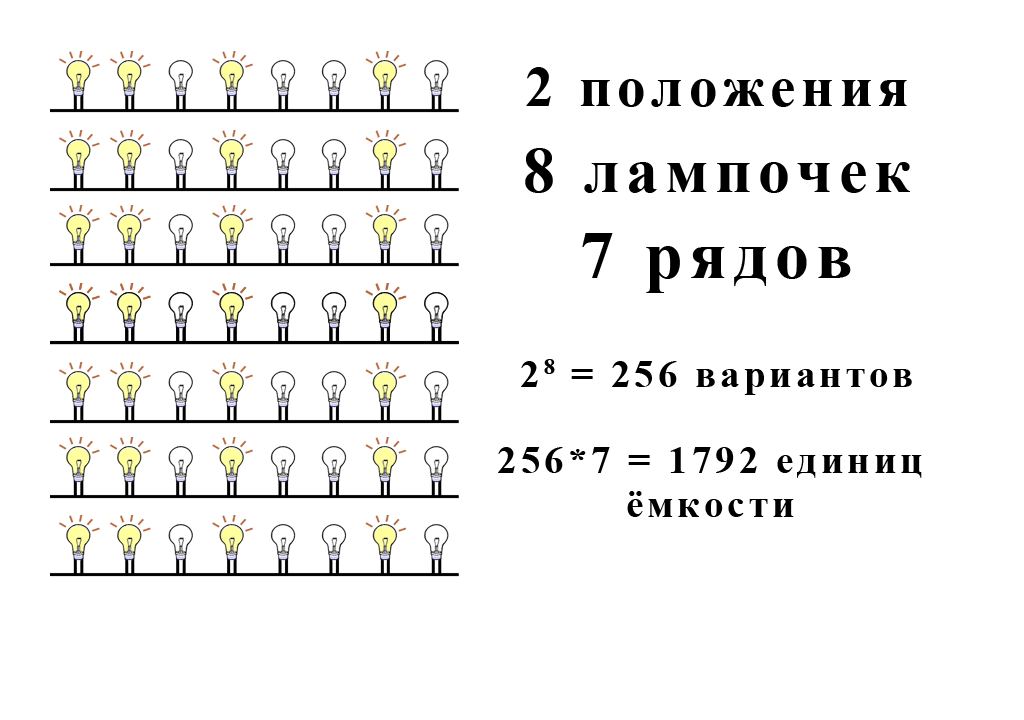
Roughly speaking, today we have a series of eight light bulbs, which use binary code as the basis.
Here is a schematic model of 1 byte consisting of 8 bits.
The structure of the cell itself implies a block of seven cells - in other words, there are fewer structural elements in my system than in the original. In my opinion, this is good, as it takes up less space, and, therefore, will significantly save the used space.
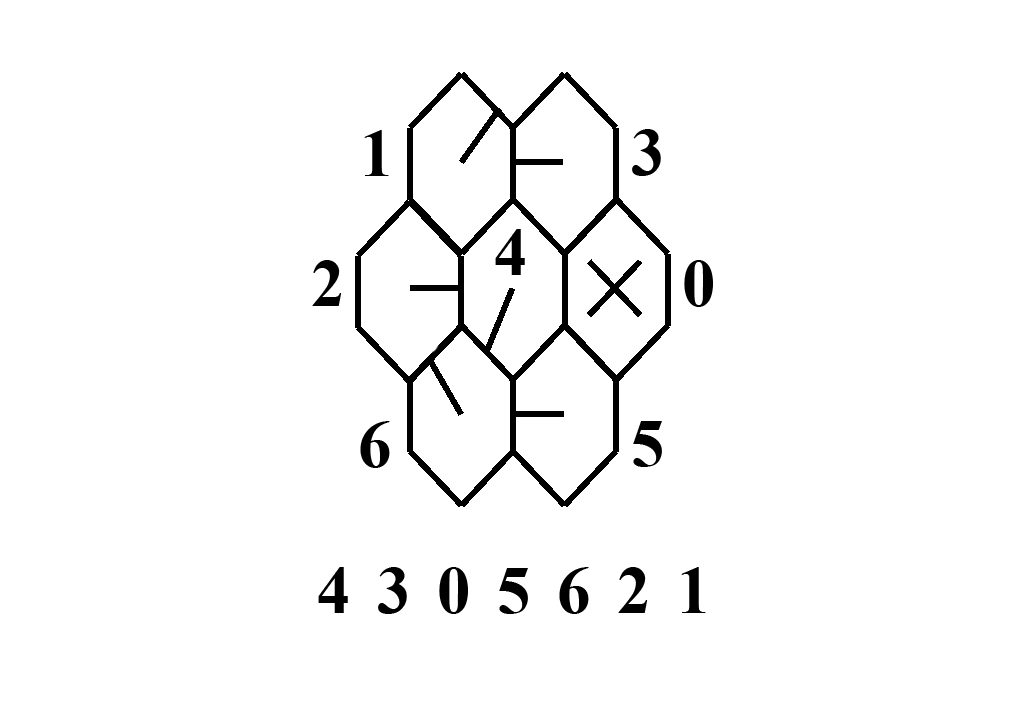
Each cell can be in 7 positions: 0, 1, 2, 3, 4, 5 and 6.
Before you is a schematic model of 1 septica, consisting of 7 septs.
Visual analysis:
For more convincing, I introduced the term “information capacity unit”, which takes into account all possible variants of bridge positions in a group of cells or all possible variants of light bulbs in byte rows.
To make it all fair, the images below examine 7 bytes and 7 septiquins, which form 1 septon.
The result is an efficiency of more than 3216 times.

PS
And finally, a few words about the classification:
1 septa (alternative to bit) - 1 hexagon (structural unit).
1 septin (alternative to byte) - a group of 7 hexagons (7 septs).
1 septon (alternative to kilobyte) - a group of 49 hexahedrons (7 septiles).
1 septoyd (alternative to gigabyte) - a group of 343 hexahedrons (7 septones or 49 septiins).
Further, there is no point in coming up with a classification, since already at the stage of septada we observe a very large amount of information.
I suppose it would be wise to introduce such concepts as a biseptoid, trisepttoid, tetraseptoid, and so on up to seven.
I hope that among those who have read, there will be a great genius who will use my concept, assemble the first “bee” computer and write to it a wonderful “honey” language based on the sevenfold code, thus occupying a niche next to such great people as Steve Jobs and Bill Gates .
Good luck! And thank you for your attention.
Recently I wondered why the binary code is being used now.
I imagined alternative reality and alternative technologies, and a very interesting concept came into my head, which I hasten to share.
Introduction:
Today we use a binary code - it is simple and reliable, but still BINARY, that is, there are only two positions “0” and “1” for encoding information.
This can be compared to a car:
- like the binary code, it was invented in the twentieth century,
- like the binary code, it rapidly developed from the right engine to the gas engine, which can be compared with the lamp and transistor systems of the elementary basis of a digital computer.
- Indeed, the car is an effective and convenient means of transportation - as well as the binary code is an effective and convenient basis for digital computing.
')
BUT it's just a car! But there is a much more complicated technique, such as helicopters and airplanes, for example.
And I am convinced that just as we mastered the sky, we will master other models of digital coding of information.
As always, the idea for the concept was presented by mother nature. Today I want to introduce you to the honeycomb technology.
Structural units:
So, for simplicity, I will give examples on a schematic lamp model.
As I said in the binary system, there are only two positions - “0” and “1”. We have one light bulb that can be lit or turned off - there is no third. A light off is “0”, and an on light is “1.”

But what if we consider a hexagon model?
Instead of a light bulb, I imagine an element in the form of a hexagon, each of the walls of which has its own conductivity. In the center of the figure is the input contact (source), each face has an output contact that is connected to a common drain, and since the faces have different conductivities, the output voltage on the drain will be different (depending on which face the charge went through).
The most interesting element of the model is the bridge. Rotating in a circle, the bridge alternately connects the center of the figure with its faces.
But this is not all, each face has its own transmitting ability of a strict range, therefore the contact will be broken as soon as the voltage exceeds the permissible limit, and the bridge immediately goes to the next edge with a higher selected transmitting range.

In chips based on TTL, “zero” is expressed by a voltage in the range from +0 to +0.8 volts, and “one” - in the range from +2.4 to +5.0 V.
The same logic can be applied to my six-sided "bee" cell:
0 - voltage range from +0 to +0.8 Volts;
1 - voltage range from +1.2 to +2.0 volts;
2 - voltage range from +2.4 to +3.2 Volts;
3 - voltage range from +3.6 to +4.4 volts;
4 - voltage range from +4.8 to +5.6 Volts;
5 - voltage range from +6.0 to +6.8 Volts;
6 - voltage range from +7.2 to +8.0 Volts;
As we can see, each of the positions of the bridge has a range of 0.8 Volts. The range in o, 4 volts after each face, is needed to protect the system from spontaneous transitions of the bridge from one face to another.

Comparison of information capacity:
Let us now compare how effective the system proposed by me in comparison with the original one.
Roughly speaking, today we have a series of eight light bulbs, which use binary code as the basis.
Here is a schematic model of 1 byte consisting of 8 bits.

The structure of the cell itself implies a block of seven cells - in other words, there are fewer structural elements in my system than in the original. In my opinion, this is good, as it takes up less space, and, therefore, will significantly save the used space.
Each cell can be in 7 positions: 0, 1, 2, 3, 4, 5 and 6.
Before you is a schematic model of 1 septica, consisting of 7 septs.

Visual analysis:
For more convincing, I introduced the term “information capacity unit”, which takes into account all possible variants of bridge positions in a group of cells or all possible variants of light bulbs in byte rows.
To make it all fair, the images below examine 7 bytes and 7 septiquins, which form 1 septon.
The result is an efficiency of more than 3216 times.


PS
And finally, a few words about the classification:
1 septa (alternative to bit) - 1 hexagon (structural unit).
1 septin (alternative to byte) - a group of 7 hexagons (7 septs).
1 septon (alternative to kilobyte) - a group of 49 hexahedrons (7 septiles).
1 septoyd (alternative to gigabyte) - a group of 343 hexahedrons (7 septones or 49 septiins).
Further, there is no point in coming up with a classification, since already at the stage of septada we observe a very large amount of information.
I suppose it would be wise to introduce such concepts as a biseptoid, trisepttoid, tetraseptoid, and so on up to seven.
I hope that among those who have read, there will be a great genius who will use my concept, assemble the first “bee” computer and write to it a wonderful “honey” language based on the sevenfold code, thus occupying a niche next to such great people as Steve Jobs and Bill Gates .
Good luck! And thank you for your attention.
Source: https://habr.com/ru/post/186154/
All Articles