Guessing the smallest unique natural number (cases of three and four players)
Hello, Habrahabr!
Not so long ago, somewhere in the open spaces of one social network, I saw the following game: players send to the moderator (let's call it that) by a whole positive number (the players do not know each other’s numbers), the one who sent the smallest unique number wins. For example, if 7 players are playing and they sent the numbers 5, 4, 2, 1, 1, 2, 6 , the player who sent the number 4 wins. It became terribly interesting to me, how it is necessary to “correctly” play this game, but it turned out that if there are unique solutions for n players here, then it is quite complicated and confusing, so let's consider specific cases for 3 and 4 players .
So let's go. To begin with, we introduce a restriction: let the players choose only numbers from {1, 2, 3} (then it will be easier and more obvious to go to the choice of any natural number). What we will try to do now is: find such a mixed strategy. that when all the players adhered to this strategy, no one could increase the chances of winning by changing their strategy (such a thing, by the way, is called the Nash equilibrium ). That is, each player with a probability
that when all the players adhered to this strategy, no one could increase the chances of winning by changing their strategy (such a thing, by the way, is called the Nash equilibrium ). That is, each player with a probability  chose the number 1 , with probability
chose the number 1 , with probability  - number 2 and with probability
- number 2 and with probability 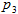 - 3 , and it would be disadvantageous for each of the players to deviate from these probabilities.
- 3 , and it would be disadvantageous for each of the players to deviate from these probabilities.
Suppose that players 2 and 3 use these probabilities, and player 1 decided to increase his chances of winning and now uses a strategy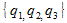 . To win, he must choose the number 1 (and the remaining players must choose either both 2 , or both 3 , or one 2 , and the second 3 ), number 2 (the rest must choose either both 1 or both 3 ), or 3 (in this case, the others must either both choose 1 or both choose 2 ). Thus, the final probability of winning
. To win, he must choose the number 1 (and the remaining players must choose either both 2 , or both 3 , or one 2 , and the second 3 ), number 2 (the rest must choose either both 1 or both 3 ), or 3 (in this case, the others must either both choose 1 or both choose 2 ). Thus, the final probability of winning 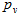 can be expressed as the sum of these three probabilities:
can be expressed as the sum of these three probabilities: 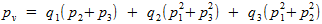 (one). Do not forget also that the sum of all probabilities is ultimately equal to one, i.e.
(one). Do not forget also that the sum of all probabilities is ultimately equal to one, i.e. 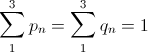 (*)
(*)
')
So, player 1 needs to try to increase his chance of winning.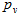 , but we have a restriction (*). The glorious Lagrange multiplier method comes to the rescue, which does just what we need — it finds local extremes of the function (we have a function (1)) with existing restrictions on certain equalities (we have an equality (*)). Lagrange equation
, but we have a restriction (*). The glorious Lagrange multiplier method comes to the rescue, which does just what we need — it finds local extremes of the function (we have a function (1)) with existing restrictions on certain equalities (we have an equality (*)). Lagrange equation  gives us the following equations:
gives us the following equations:
 ,
,
which we decide, taking into account, of course, equality (*). We get the following probabilities:

Done! What is the conclusion? When 3 players can choose only from {1, 2, 3} , for each of them the optimal strategy will be the following: in half the cases choose 1 , approximately in a quarter - choose 2 , and in approximately a quarter - 3 . This will be the Nash equilibrium.
So, what happens if we remove the restrictions on the set, from which players can choose numbers and how do we find Nash equilibrium for such a game? Now, if a player chooses a certain number i , he will win only if all the players choose the same number strictly less than i , or both choose by the number, each of which is strictly greater than i . Thus, for each player, the probability of winning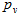 next:
next:  . Differentiating this equation, we get an infinite set of equations:
. Differentiating this equation, we get an infinite set of equations: 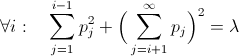 and restriction
and restriction  . Such a thing is solved, but it is rather difficult, so I’ll just give here the answer:
. Such a thing is solved, but it is rather difficult, so I’ll just give here the answer:
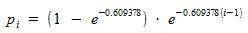 .
.
What does all of this mean? If we substitute concrete numbers into the resulting equation, then for the first seven we get approximately the following probabilities:
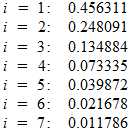
That is, the Nash equilibrium will be a set of strategies where each player with a probability of approximately 0.46 chooses 1 , with a probability of 0.25 - 2 , with a probability of 0.13 - 3 , and so on.
The same game, with four players, is not much different from a game with three. In this case, the function to be maximized is as follows:

What is what?

The solution is as follows:
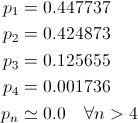
From this it follows that most often you will have to choose the numbers 1 and 2 , occasionally - 3 , very rarely - 4 , and it is almost impossible to deal with numbers more than four.
Thanks for attention. Play games.
Not so long ago, somewhere in the open spaces of one social network, I saw the following game: players send to the moderator (let's call it that) by a whole positive number (the players do not know each other’s numbers), the one who sent the smallest unique number wins. For example, if 7 players are playing and they sent the numbers 5, 4, 2, 1, 1, 2, 6 , the player who sent the number 4 wins. It became terribly interesting to me, how it is necessary to “correctly” play this game, but it turned out that if there are unique solutions for n players here, then it is quite complicated and confusing, so let's consider specific cases for 3 and 4 players .
The case of three players
Selection from {1, 2, 3}
So let's go. To begin with, we introduce a restriction: let the players choose only numbers from {1, 2, 3} (then it will be easier and more obvious to go to the choice of any natural number). What we will try to do now is: find such a mixed strategy.
 that when all the players adhered to this strategy, no one could increase the chances of winning by changing their strategy (such a thing, by the way, is called the Nash equilibrium ). That is, each player with a probability
that when all the players adhered to this strategy, no one could increase the chances of winning by changing their strategy (such a thing, by the way, is called the Nash equilibrium ). That is, each player with a probability  chose the number 1 , with probability
chose the number 1 , with probability  - number 2 and with probability
- number 2 and with probability 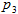 - 3 , and it would be disadvantageous for each of the players to deviate from these probabilities.
- 3 , and it would be disadvantageous for each of the players to deviate from these probabilities.Suppose that players 2 and 3 use these probabilities, and player 1 decided to increase his chances of winning and now uses a strategy
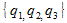 . To win, he must choose the number 1 (and the remaining players must choose either both 2 , or both 3 , or one 2 , and the second 3 ), number 2 (the rest must choose either both 1 or both 3 ), or 3 (in this case, the others must either both choose 1 or both choose 2 ). Thus, the final probability of winning
. To win, he must choose the number 1 (and the remaining players must choose either both 2 , or both 3 , or one 2 , and the second 3 ), number 2 (the rest must choose either both 1 or both 3 ), or 3 (in this case, the others must either both choose 1 or both choose 2 ). Thus, the final probability of winning 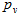 can be expressed as the sum of these three probabilities:
can be expressed as the sum of these three probabilities: 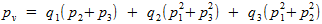 (one). Do not forget also that the sum of all probabilities is ultimately equal to one, i.e.
(one). Do not forget also that the sum of all probabilities is ultimately equal to one, i.e. 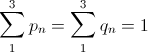 (*)
(*)')
So, player 1 needs to try to increase his chance of winning.
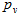 , but we have a restriction (*). The glorious Lagrange multiplier method comes to the rescue, which does just what we need — it finds local extremes of the function (we have a function (1)) with existing restrictions on certain equalities (we have an equality (*)). Lagrange equation
, but we have a restriction (*). The glorious Lagrange multiplier method comes to the rescue, which does just what we need — it finds local extremes of the function (we have a function (1)) with existing restrictions on certain equalities (we have an equality (*)). Lagrange equation  gives us the following equations:
gives us the following equations: ,
,which we decide, taking into account, of course, equality (*). We get the following probabilities:

Done! What is the conclusion? When 3 players can choose only from {1, 2, 3} , for each of them the optimal strategy will be the following: in half the cases choose 1 , approximately in a quarter - choose 2 , and in approximately a quarter - 3 . This will be the Nash equilibrium.
The choice of any natural number
So, what happens if we remove the restrictions on the set, from which players can choose numbers and how do we find Nash equilibrium for such a game? Now, if a player chooses a certain number i , he will win only if all the players choose the same number strictly less than i , or both choose by the number, each of which is strictly greater than i . Thus, for each player, the probability of winning
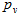 next:
next:  . Differentiating this equation, we get an infinite set of equations:
. Differentiating this equation, we get an infinite set of equations: 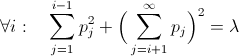 and restriction
and restriction  . Such a thing is solved, but it is rather difficult, so I’ll just give here the answer:
. Such a thing is solved, but it is rather difficult, so I’ll just give here the answer: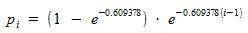 .
.What does all of this mean? If we substitute concrete numbers into the resulting equation, then for the first seven we get approximately the following probabilities:
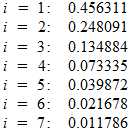
That is, the Nash equilibrium will be a set of strategies where each player with a probability of approximately 0.46 chooses 1 , with a probability of 0.25 - 2 , with a probability of 0.13 - 3 , and so on.
The case of four players
The same game, with four players, is not much different from a game with three. In this case, the function to be maximized is as follows:

What is what?

The solution is as follows:
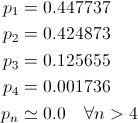
From this it follows that most often you will have to choose the numbers 1 and 2 , occasionally - 3 , very rarely - 4 , and it is almost impossible to deal with numbers more than four.
Thanks for attention. Play games.
Source: https://habr.com/ru/post/185862/
All Articles