So you still don't understand Hindley-Milner? Part 2
In Part 1, we talked about what building blocks are needed to formalize Hindley-Milner, and in this post we specify their definitions and formulate the formalization as a whole:
We will give a recursive definition of what an expression is; in other words, we will define most of the types of expressions, describe how to create new, more complex expressions, based on existing ones, and show that only valid expressions can be created in this way.
Nothing is more than a valid expression.
')
Aside: anyone who pays enough attention to this question will be surprised: “Just a minute, how can I make some useful expression out of this? How can I get
Let
Then, if
Like
We can give a formal definition of what is considered a type, as we did above for expressions. However, the abstraction in this case is quite intricate, so we omit this moment. I simply draw your attention to two key points that should be kept in mind:
Now we want to formalize a branch of rules on how we can proceed from the knowledge of some expressions and their types to the derivation of the types of a greater number of expressions. Remember how sentence calculus formulates Modus Ponens? We are going to do something similar. For example, suppose we want to formalize the following part of the reasoning:
We formalize it as follows:
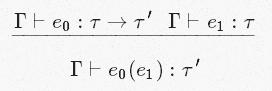
This rule is called [App] (for overlays), and it is one of those that are present in this issue on StackOverflow . We will talk about him and the remaining rules in the next post. In the meantime, let's deal with all the characters that we met above:
Next step:
Translator's note: I would be very grateful for any comments in PM about the translation.
Formalization of the concept of expression
We will give a recursive definition of what an expression is; in other words, we will define most of the types of expressions, describe how to create new, more complex expressions, based on existing ones, and show that only valid expressions can be created in this way.
- Variables are valid expressions.
- If
eis an arbitrary expression, andxis an arbitrary variable, thenλx.eis an expression. Here it helps to think abouteas an ordinary (but not necessarily) complex expression that includesx, i.e.x²+2, and then aboutλx.eas an anonymous function, which takes inputxand returns the result of evaluating the expressionefor the given valuex. Simply put, think of it asfunction(x) { return x^2 + 2; } - if
fandeare valid expressions, thenf(e)also valid. It is called an “overlay” ( Application ) for obvious reasons. - If
xis a variable, ande1 ande0 are valid expressions, then replacing every occurrence ofxine0 withe1 will also give a valid expression. That is, if, for example,e1 =x²+2ande0 =y/3, then puttingx=e0 ine1 , we get the expression(y/3)²+2.
[NB: The last item is redundant and is not officially included in the definition of lambda calculus for expressions, since the substitution ofe0 asxine1 is equivalent to using the abstractionλx.e1 toe0 . It is added only to support so-called let polymorphism .]
Nothing is more than a valid expression.
')
Aside: anyone who pays enough attention to this question will be surprised: “Just a minute, how can I make some useful expression out of this? How can I get
x 2 +2 (or at least 2), based on the above? Damn, what about zero? There is no line in these rules, which obviously leads to the expression 0 ". The solution in this case is to create an expression in lambda calculus that behaves like 0.1, ..., +, ×, -, / with the correct interpretation. In other words, we should encode numbers, arithmetic operations, strings, etc. into patterns that we can create using lambda syntax. In this post there is a small, but very good section on numbers and arithmetic operations. This is an interesting feature of lambda calculus: we have an elementary syntax that we can recursively define with four simple points, but it allows us to inductively prove many things in four basic steps, since the language itself has expressive power to write numbers, strings and all types operations that we may need.Formalization of type statements
Let
e be any expression such that " e " is a variable in our meta-language, denoting any expression from our base language. For example, such as any of the following: x Math.pow(x,2) [1,2].forEach ( function(x) { print(x); } ) Then, if
t is an arbitrary type, then we can express " e has type t " throughe:tLike
e , t is a variable in our meta-language that can correspond to any type in the base language (int, string, etc.). And just like for e , for t compliance with any particular type is not required.We can give a formal definition of what is considered a type, as we did above for expressions. However, the abstraction in this case is quite intricate, so we omit this moment. I simply draw your attention to two key points that should be kept in mind:
- If
sandtare types, thent→s;Is the type of the function withtat the input andsat the output - If
ris a type, possibly composed of other types (just ast→sis composed oftands,each of which, in turn, can potentially be represented as a composition of some other types), andαis a variable of this type, then ∀α.ris a type.
Without an example, the above sounds a bit pointless:function (x) { return x; }
This function is of typeString→String. OrInt→Int. In fact, for any typetits type ist→t. We will say that it is of type ∀tt→t. Each of the typesString→Stringort→tis a “monotype”. ∀tt→tis a “polytype”. The function identical to that written above has an abstract polytype ∀tt→t, which in practice means that for any real typetit has typet→t. Putting all of the above together, we get just such a compact summary record:
λxx:∀α.α→α
Formalization of statements about statements about types
Now we want to formalize a branch of rules on how we can proceed from the knowledge of some expressions and their types to the derivation of the types of a greater number of expressions. Remember how sentence calculus formulates Modus Ponens? We are going to do something similar. For example, suppose we want to formalize the following part of the reasoning:
Suppose I am already able to infer that the variableduckis of typeAnimal.
Moreover, suppose that I deduced thatspeakis a method of typeAnimal->String.
Then I can deduce thatspeak(duck)is of typeString.
And any reasoning that fits into such a form is a valid type inference.
We formalize it as follows:
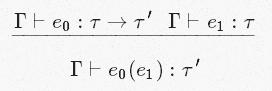
This rule is called [App] (for overlays), and it is one of those that are present in this issue on StackOverflow . We will talk about him and the remaining rules in the next post. In the meantime, let's deal with all the characters that we met above:
- Γ - corresponds to a set of positions that we already know, or maybe we can assume. More generally, Γ is just a reflection on a certain collection of positions (on expressions and their types). And naturally, there is nothing special about the letter Γ - capital Greek letters are often used to designate sets of positions.
- ⊢ - “turnstile”, meaning that something can be displayed. For example, Γ ⊢
x:tmeans that if we take a statement from Γ as an assumption / axiom / existing knowledge, then we can infer thatxis of typet. - ∈ - "epsilon", means belonging to something.
x:t∈ Γ says that the statementx:tbelongs to Γ. - That long horizontal line. This line tells us that we can draw conclusions, located in the denominator, if we take the numerator as the original premise. Which allows us to express things like: "If we can derive this and this, then we can also derive this and that." For example:
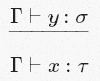
If we can infer thatyhas type σ from Γ, then we can infer thatxhas type τ from Γ.
Next step:
- Part 3 , in which we will put everything together and get an idea of the rules used in the HM algorithm.
Translator's note: I would be very grateful for any comments in PM about the translation.
Source: https://habr.com/ru/post/185686/
All Articles