So you still don't understand Hindley-Milner? Part 1
Once we sat in a bar with Josh Long and a few other friends from work when he discovered that I was on “hey, you!” With math. And he just recently stumbled upon this question on StackOverflow and now asked me what it means:
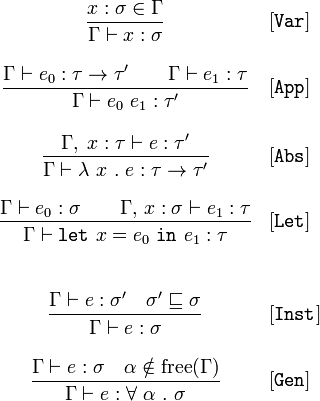
However, before figuring out the meaning of this Chinese literacy, I think it is, in principle, worth getting an idea of why it is needed at all. A post on Daniel Spivak's blog ( translation ) gives a really good explanation of the ultimate goal of the Hindley-Milner algorithm (in addition to the in-depth example of its use):
So, we want to formalize the type inference algorithm for any given expression. In this post, I'm going to dwell on what it means to “formalize something” and then describe the “bricks” of the Hindley-Milner formalization. In the second part I will give a more specific description of these blocks. Finally, in the third part I will translate the question from StackOverflow.
So we are going to talk about expressions. Arbitrary expressions. In any language. We also want to talk about type inference for these expressions. And we want to find out the rules by which we could infer types. And then we want to create an algorithm that would use these rules for type inference. So we need some meta language. Such that with its help it was possible to speak about expression in any arbitrary programming language. This meta language should:
To give the above more specifics, let's consider a very short example of formalization. What if instead of formalizing a language for talking about the derivation of types of expressions in an arbitrary programming language, we want to formalize a language for talking about the truth of a statement in an arbitrary natural language? Without formalization, we could say something like:
Calculating sentences formalizes all of these things in the form of a rule known as Modus Ponens (“inference rule”):
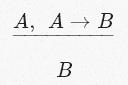
where
And now let's list the building blocks of the Hindley-Milner formalization:
We will need:
Well, let's go!
Translator's note: I would be very grateful for any comments in PM about the translation.
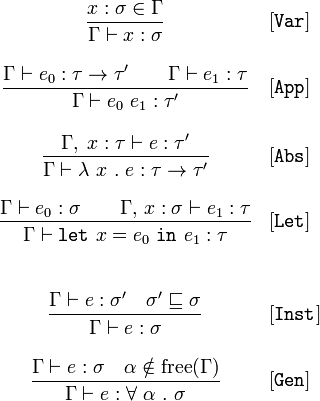
However, before figuring out the meaning of this Chinese literacy, I think it is, in principle, worth getting an idea of why it is needed at all. A post on Daniel Spivak's blog ( translation ) gives a really good explanation of the ultimate goal of the Hindley-Milner algorithm (in addition to the in-depth example of its use):
Functionally speaking, Hindley-Milner (or Damas-Milner) is an algorithm for inferring types based on how they are used. He literally formalizes the intuitive knowledge that the type can be derived through the functionality that it supports.
So, we want to formalize the type inference algorithm for any given expression. In this post, I'm going to dwell on what it means to “formalize something” and then describe the “bricks” of the Hindley-Milner formalization. In the second part I will give a more specific description of these blocks. Finally, in the third part I will translate the question from StackOverflow.
What does “formalize” mean?
So we are going to talk about expressions. Arbitrary expressions. In any language. We also want to talk about type inference for these expressions. And we want to find out the rules by which we could infer types. And then we want to create an algorithm that would use these rules for type inference. So we need some meta language. Such that with its help it was possible to speak about expression in any arbitrary programming language. This meta language should:
- To be abstract and general in order to allow us to reason about the statements of type inference, proceeding solely from their form (hence the formalization ), without worrying about the content
- Giving an accurate, unambiguous, but intuitive definition of what an expression is
- To give this definition in terms of a small number of undisputed primitive concepts.
- Similarly, define for types, the idea that an expression has a type, and the idea that we can infer that the expression has a given type
- Give in to a simple, brief symbolic representation. Those. instead of saying “an expression formed by applying the first expression to the second expression, has the type of a function from a string to some type that we do not need to specialize in this context”, we can simply say "
e1 (e2 ):String→t" - Easily translated into something that a computer can understand and implement so that they can fully automate type inference.
To give the above more specifics, let's consider a very short example of formalization. What if instead of formalizing a language for talking about the derivation of types of expressions in an arbitrary programming language, we want to formalize a language for talking about the truth of a statement in an arbitrary natural language? Without formalization, we could say something like:
Suppose I know that if it rains, Bob always takes an umbrella.
And suppose I know it is raining now.
So I can conclude that Bob took an umbrella.
')
And any argument that has the same form is valid for a similar conclusion.
Calculating sentences formalizes all of these things in the form of a rule known as Modus Ponens (“inference rule”):
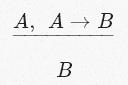
where
And now let's list the building blocks of the Hindley-Milner formalization:
Building blocks formalization
We will need:
- The formal way to talk about expressions. This formalization must meet the criteria listed above; for this purpose we use lambda calculus . I will explain everything literally in a minute, but there is nothing supernatural
- The formal way to talk about types, and the formal way to talk about types and expressions together. In the end, the goal of the Hindley-Milner algorithm is to be able to infer the conclusion “the expression
ehas typet” - A formal set of rules for obtaining statements about the type of expression through other statements. These rules are like: “if I can already demonstrate that a certain expression has one type, and another expression has a second type, then the third expression will have a third type”. This set of rules is exactly what you see in the question with StackOverflow . I will translate it in detail
- The algorithm should reasonably use the inference rules to derive the required statement from the starting point: “The expression
einterests me is of typet”. The “algorithm” part in the phrase “Hindley-Milner's algorithm” is responsible for this, and in these posts I do not plan to discuss this issue.
Well, let's go!
- Part 2 , in which we clearly define points 1 and 2
- Part 3 , in which we translate the type inference rules from clause 3
Translator's note: I would be very grateful for any comments in PM about the translation.
Source: https://habr.com/ru/post/185362/
All Articles