Entertaining C ++: Compile Time Counter
It is proposed to develop a safe alternative to the built-in macro
Unfortunately, the macro
You need the ability to use local counters instead of a single global (at least for each header file its own). In this case, the ability to use the value of the counter in a constant expression should be preserved.
')
Based on this question on Stack Overflow.
Summarizing - we have an expression with a function call. Add the definition of the overloaded function, as a result, the compiler uses a new function. Thus, the type of the return value from the function and the type of the whole expression changed, although the textual expression remained the same.
Define macros to read and “increment” a one-bit counter.
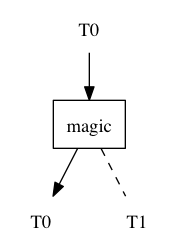
Here it is, our basic building block. This is a function of a single argument of type T 0 . Depending on the available declarations in scope, the return type is either T 0 or T 1 . This device resembles an arrow on the rail. In the initial state, the "arrow" is directed to the left. "Arrow" can be switched only once.
Using several basic blocks, we can build an extensive network:
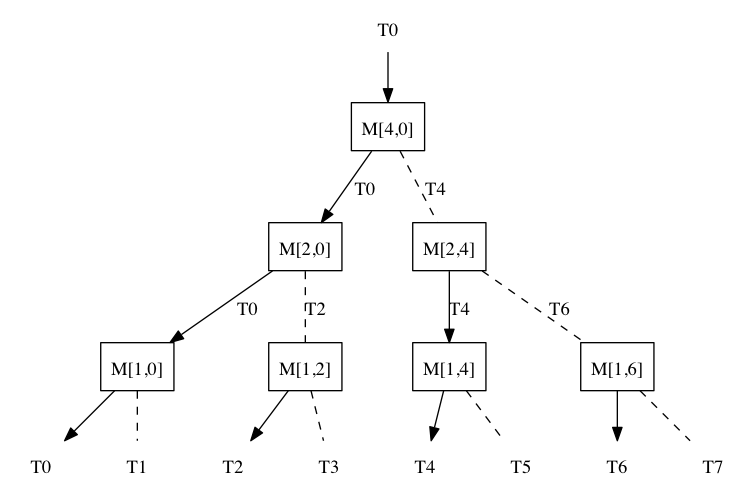
When searching for a suitable variant of a function, the C ++ compiler takes into account only the types of parameters and ignores the type of the returned value. If the expression has nested function calls, the compiler “moves” from the inside to the outside. For example, in the following expression: M 1 (M 2 (M 4 (T 0 ()))), the compiler first allows (“resolves”) the call to the function M 4 (T 0 ). Then, depending on the type of return value of the function M 4 , it allows the call M 2 (T 0 ) or M 2 (T 4 ), and so on.
Continuing the railway analogy, we can say that the compiler moves from top to bottom along the railway network, “turning” on the arrows to the right or left. An expression of N nested function calls generates a network with 2 N outputs. By switching the arrows in the correct order, you can consistently get all 2 N possible types T i at the output of the network.
It can be shown that if the current type is at the output of the network T i , then the next one needs to switch the arrowM [(i + 1) & ~ i, (i + 1) & i] .
The final version of the code is available here .
How practical are these solutions?
IMHO if a single C ++ file is compiled for more than 5 minutes, and only the latest version of the compiler can handle it - this is definitely impractical . Many "creative" uses of language features in C ++ are of academic interest only. As a rule, the same tasks can be better solved in other ways, for example, by using an external code generator. Although, I must say, the author is somewhat biased in this matter, categorically not recognizing the spirit , and experiencing some weakness in relation to bison .
It seems that the compile time counter is also not very practical, as can be clearly seen in the following graph. The x- axis represents the absolute value of the increment of the counter in the test program (the test program consists of the lines

__COUNTER__ . The first macro entry is replaced with 0 , the second with 1 , and so on. The value __COUNTER__ substituted at the preprocessing stage, therefore it can be used in the context of a constant expression .Unfortunately, the macro
__COUNTER__ dangerous to use in header files - with a different order of inclusion of header files, the substituted counter values will change. This can lead to a situation where, for example, in foo.cpp value of the AWESOME constant is 42, while in bar.cpp AWESOME≡33 . This is a violation of the principle of one definition rule, that there is a terrible crime in the C ++ universe.You need the ability to use local counters instead of a single global (at least for each header file its own). In this case, the ability to use the value of the counter in a constant expression should be preserved.
')
Based on this question on Stack Overflow.
Motivating example
When is the compile time counter useful?
Suppose we want to implement macros to define simple data structures with serialization support. It might look something like this:
Here we do not just define a
Unfortunately, we need to go through the list of fields at least two times: to create field definitions and to generate the serialization function. With the help of the preprocessor alone, this cannot be done. But as you know, any problem in C ++ can be solved with the help of templates (except for the problem of oversupply of templates).
Define the
When expanding
When expanding
Each subsequent occurrence of the
Under the link a working code sample.
STRUCT(Point3D) FIELD(x, float) FIELD(y, float) FIELD(z, float) END_STRUCT Here we do not just define a
Point3D structure with a list of x, y and z fields. We also automatically get the serialization and deserialization functions. It is impossible to add a new field and forget serialization support for it. You have to write much less than for example for boost .Unfortunately, we need to go through the list of fields at least two times: to create field definitions and to generate the serialization function. With the help of the preprocessor alone, this cannot be done. But as you know, any problem in C ++ can be solved with the help of templates (except for the problem of oversupply of templates).
Define the
FIELD macro as follows (for clarity, use __COUNTER__ ): #define FIELD(name, type) \ type name; // \ template<> \ void serialize<__COUNTER__/2>(Archive &ar) { \ ar.write(name); \ serialize<(__COUNTER__-1)/2+1>(ar); \ } When expanding
FIELD(x, float) will turn out float x; // x template<> void serialize<0>(Archive &ar) { ar.write(x); serialize<1>(ar); } When expanding
FIELD(y, float) turns out float y; // y template<> void serialize<1>(Archive &ar) { ar.write(x); serialize<2>(ar); } Each subsequent occurrence of the
FIELD() macro expands to the field definition, plus the specialization of the function serialize< i >() where i = 0,1,2, ... N. The function serialize<i>() calls serialize<i+1>() , and so on. The counter helps to connect the disparate functions together.Under the link a working code sample.
One-bit Compile Time Counter
To begin with, we will show implementation of the one-bit counter. // (1) template<size_t n> struct cn { char data[n+1]; }; // (2) template<size_t n> cn<n> magic(cn<n>); // (3) sizeof(magic(cn<0>())) - 1; // 0 // (4) «» cn<1> magic(cn<0>); // (5) sizeof(magic(cn<0>())) - 1; // 1 - We define the template structure
cn<n>. Note thatsizeof(cn<n>) ≡ n+1. - We define the template
magicfunction. - The
sizeofoperator applied to an expression returns the size of the type that this expression has. Since the expression is not evaluated, the body definition of themagicfunction is not required.
The only currently definedmagicfunction is a template from p. 2. Therefore, the type of the return value and the entire expression iscn<0>. - Define the overloaded
magicfunction. Note that ambiguities do not occur whenmagiccalled, because overloaded functions take precedence over template functions. - Now, when calling
magic(cn<0>()), another version of the function will be used; expression type insidesizeof-cn<1>().
Summarizing - we have an expression with a function call. Add the definition of the overloaded function, as a result, the compiler uses a new function. Thus, the type of the return value from the function and the type of the whole expression changed, although the textual expression remained the same.
Define macros to read and “increment” a one-bit counter.
#define counter_read(id) \ (sizeof(magic(cn<0>())) - 1) #define counter_inc(id) \ cn<1> magic(cn<0>) about id parameter
According to the plan, the id parameter allows you to use several independent counters, by defining unique types and using them as id . For id support, the
magic function must take the additional id parameter. The overloaded magic functions will be related to a specific id , and will not affect all other id's .N-bit compile time counter
N-bit counter is based on the same principles as one-bit. Instead of onemagic call inside sizeof , we will have a chain of nested calls a(b(c(d(e( … ))))).
Here it is, our basic building block. This is a function of a single argument of type T 0 . Depending on the available declarations in scope, the return type is either T 0 or T 1 . This device resembles an arrow on the rail. In the initial state, the "arrow" is directed to the left. "Arrow" can be switched only once.
Using several basic blocks, we can build an extensive network:

When searching for a suitable variant of a function, the C ++ compiler takes into account only the types of parameters and ignores the type of the returned value. If the expression has nested function calls, the compiler “moves” from the inside to the outside. For example, in the following expression: M 1 (M 2 (M 4 (T 0 ()))), the compiler first allows (“resolves”) the call to the function M 4 (T 0 ). Then, depending on the type of return value of the function M 4 , it allows the call M 2 (T 0 ) or M 2 (T 4 ), and so on.
Continuing the railway analogy, we can say that the compiler moves from top to bottom along the railway network, “turning” on the arrows to the right or left. An expression of N nested function calls generates a network with 2 N outputs. By switching the arrows in the correct order, you can consistently get all 2 N possible types T i at the output of the network.
It can be shown that if the current type is at the output of the network T i , then the next one needs to switch the arrow
The final version of the code is available here .
Instead of conclusion
The compile time counter is entirely based on the overloaded functions mechanism. This technique I spied on Stack Overflow. As a rule, non-trivial compile-time calculations in C ++ are implemented on templates, which is why the presented solution is especially interesting, since instead of templates it exploits other mechanisms.How practical are these solutions?
IMHO if a single C ++ file is compiled for more than 5 minutes, and only the latest version of the compiler can handle it - this is definitely impractical . Many "creative" uses of language features in C ++ are of academic interest only. As a rule, the same tasks can be better solved in other ways, for example, by using an external code generator. Although, I must say, the author is somewhat biased in this matter, categorically not recognizing the spirit , and experiencing some weakness in relation to bison .
It seems that the compile time counter is also not very practical, as can be clearly seen in the following graph. The x- axis represents the absolute value of the increment of the counter in the test program (the test program consists of the lines
counter_inc(int) ), the y -axis - the compilation time in seconds. For comparison, the compilation time of nginx-1.5.2 is also postponed there.
Source: https://habr.com/ru/post/184800/
All Articles