Ragdoll physics do-it-yourself. Part one
Once I decided to write a game. For yourself and for your pleasure. There was a choice in front of me - to use all the ready aka Box2D or write the physics for it myself. The second option seemed to me more interesting, and I began to look for information in the open spaces of the network that would help me write everything I needed. I found. As a result, a very flexible (as for the game) and simple physics engine was obtained. The basis of the engine was the Verlet numerical integration method.

Werle's method describes the movement of material points in time. For this there are different methods. For example, such a system of equations.
')

Combining 2 equations, we get
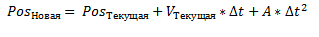
The Verlet equation is not much different from the above entry.

As you can see, in the Verlet method, the velocity of a point is expressed in terms of the difference between its current and old coordinates. Great, we have less trouble. The accuracy of calculations from this decreases, but we are not counting atomic reactors. Plus it makes collision calculation so ridiculously simple. Consider the movement of a point by example:
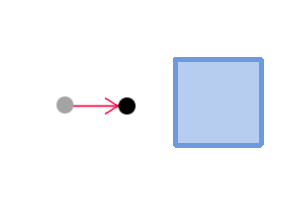
We see that the current and old coordinates of the point are chosen in such a way that it inevitably moves to the right towards the blue square. Looking forward a bit, I’ll say that when a collision with a square is detected, to handle this collision it’s enough to bring the current coordinate of the point outside the square. Everything. Since the speed here is expressed in terms of the difference of coordinates, a change in the current or old coordinate automatically leads to a change in the speed of movement of a point.

If you put all this into C ++ code, you get something like that.
This is enough to describe the movement of material points. And it’s good if you only plan points in the game. If you want something more interesting, you need to make solid bodies. In nature, a solid body is a lot of point-atoms, interconnected by the mystical forces of nature. Alas, for the simulation of physics in the game, this method is poorly suited, not a single computer will be able to withstand the calculations of billions and billions of points and connections between them. Therefore, we will manage by modeling the vertices of physical bodies. For a square this way 4 points and connections between them will be enough. It remains only to describe these links. Obviously, the distance between the vertices should remain constant. If the distance between the peaks will change, the body will be deformed, but we do not want it (those who want it while they are silent). How to keep the distance between peaks constant? In reality, to solve this problem, it would be enough to shove a reinforcement of the appropriate length between the vertices. Without further ado, we will do the same in our simulation. Let's create a class that will describe this imaginary reinforcement, keeping the vertices at the required distance. The algorithm that performs this work will be called immediately after processing the motion of the vertex points. In essence, it is very simple. We calculate the vector between two vertices connected by our imaginary reinforcement and compare the length of this vector with our reference length. If the lengths are different, we just have to move / move the vertices to the required distance, so that the lengths will coincide again and voila - it's in the bag.
This is how it all looks in the code:
This is how it is. If you create several vertices and connect them together with such sides, the resulting body will exhibit the properties of a solid body, including rotation caused by collision with other bodies and the floor. How does all this work? After all, we just added a new rule to maintain the distance between points, and here on - just a solid body. The secret is in the very method of integrating Verlet. As we remember, this method does not operate with speeds, instead it uses the difference between the coordinates of the current and the old position of the point. As a result, the speed will also change as the coordinate changes. And to maintain a constant length between the vertices, we just change their coordinates. The final change in the velocity of the vertices gives an effect that is approximately reminiscent of the behavior of solids. More precisely almost solid. In the form in which the code is now, the body will be deformed when it hits the floor and each other. Why? Everything is very simple. If the vertex is attached to more than one side, and usually will occur, the adjustment of the length of one of the sides will automatically lead to a change in the length of the other side.

The only method of treating this disease is the multiple challenge of the function, the corrective length of the parties. The more times it is called, the more accurate the approximation will be. How many times to do it depends only on your imagination. This concludes the first part of the article. The next part will cover such moments as the detection and handling of collisions between bodies and also some feints with ears that can be done using this method.

Werle's method describes the movement of material points in time. For this there are different methods. For example, such a system of equations.
')

Combining 2 equations, we get
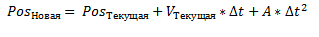
The Verlet equation is not much different from the above entry.

As you can see, in the Verlet method, the velocity of a point is expressed in terms of the difference between its current and old coordinates. Great, we have less trouble. The accuracy of calculations from this decreases, but we are not counting atomic reactors. Plus it makes collision calculation so ridiculously simple. Consider the movement of a point by example:

We see that the current and old coordinates of the point are chosen in such a way that it inevitably moves to the right towards the blue square. Looking forward a bit, I’ll say that when a collision with a square is detected, to handle this collision it’s enough to bring the current coordinate of the point outside the square. Everything. Since the speed here is expressed in terms of the difference of coordinates, a change in the current or old coordinate automatically leads to a change in the speed of movement of a point.

If you put all this into C ++ code, you get something like that.
struct Point { Vec2 Position; Vec2 OldPosition; Vec2 Acceleration; }; class Physics { int PointCount; Point* Points[ MAX_VERTICES ]; float Timestep; public: void UpdateVerlet(); }; void Physics::UpdateVerlet() { for( int I = 0; I < PointCount; I++ ) { Point& P = *Points[ I ]; Vec2 Temp = P.Position; P.Position += P.Position - P.OldPosition + P.Acceleration*Timestep*Timestep; P.OldPosition = Temp; } } This is enough to describe the movement of material points. And it’s good if you only plan points in the game. If you want something more interesting, you need to make solid bodies. In nature, a solid body is a lot of point-atoms, interconnected by the mystical forces of nature. Alas, for the simulation of physics in the game, this method is poorly suited, not a single computer will be able to withstand the calculations of billions and billions of points and connections between them. Therefore, we will manage by modeling the vertices of physical bodies. For a square this way 4 points and connections between them will be enough. It remains only to describe these links. Obviously, the distance between the vertices should remain constant. If the distance between the peaks will change, the body will be deformed, but we do not want it (those who want it while they are silent). How to keep the distance between peaks constant? In reality, to solve this problem, it would be enough to shove a reinforcement of the appropriate length between the vertices. Without further ado, we will do the same in our simulation. Let's create a class that will describe this imaginary reinforcement, keeping the vertices at the required distance. The algorithm that performs this work will be called immediately after processing the motion of the vertex points. In essence, it is very simple. We calculate the vector between two vertices connected by our imaginary reinforcement and compare the length of this vector with our reference length. If the lengths are different, we just have to move / move the vertices to the required distance, so that the lengths will coincide again and voila - it's in the bag.
This is how it all looks in the code:
struct Edge { Vertex* V1; Vertex* V2; float OriginalLength; }; void Physics::UpdateEdges() { for( int I = 0; I < EdgeCount; I++ ) { Edge& E = *Edges[ I ]; // Vec2 V1V2 = E.V2->Position - E.V1->Position; float V1V2Length = V1V2.Length(); // float Diff = V1V2Length - E.OriginalLength; V1V2.Normalize(); // E.V1->Position += V1V2*Diff*0.5f; E.V2->Position -= V1V2*Diff*0.5f; } } This is how it is. If you create several vertices and connect them together with such sides, the resulting body will exhibit the properties of a solid body, including rotation caused by collision with other bodies and the floor. How does all this work? After all, we just added a new rule to maintain the distance between points, and here on - just a solid body. The secret is in the very method of integrating Verlet. As we remember, this method does not operate with speeds, instead it uses the difference between the coordinates of the current and the old position of the point. As a result, the speed will also change as the coordinate changes. And to maintain a constant length between the vertices, we just change their coordinates. The final change in the velocity of the vertices gives an effect that is approximately reminiscent of the behavior of solids. More precisely almost solid. In the form in which the code is now, the body will be deformed when it hits the floor and each other. Why? Everything is very simple. If the vertex is attached to more than one side, and usually will occur, the adjustment of the length of one of the sides will automatically lead to a change in the length of the other side.

The only method of treating this disease is the multiple challenge of the function, the corrective length of the parties. The more times it is called, the more accurate the approximation will be. How many times to do it depends only on your imagination. This concludes the first part of the article. The next part will cover such moments as the detection and handling of collisions between bodies and also some feints with ears that can be done using this method.
Source: https://habr.com/ru/post/184724/
All Articles