Tasks with beautiful solutions
There is a class of problems, which are mainly passed from mouth to mouth, it can be said are included in mathematical folklore. Sometimes there are tasks with very beautiful solutions. You look at the decision, you seem to understand every step in the reasoning, but you feel as if you are deceived. You understand everything and at the same time do not understand anything. An analogy can probably be drawn, for example, with this optical illusion:

Here you see a big cube with a cut piece, then a small cube standing in the corner.
In this post I have collected some of my favorite tasks, the solutions of which, it seems to me, cause this elusive dualism of feelings: “I understand - I don't understand”.
Prove that using only one ruler you cannot find the center of a circle drawn on a plane (it is believed that the ruler has infinite length; it can connect any given points on the plane; there is no scale on the ruler, and nothing can be marked on it).
')
In the Moscow metro there is a rule that prohibits bringing objects, the sum of the height, width and depth of which is greater see Let's agree that we are talking about rectangular boxes. Prove that it is impossible to deceive the system and completely thrust the box, the sum of the measurements of which is greater
see Let's agree that we are talking about rectangular boxes. Prove that it is impossible to deceive the system and completely thrust the box, the sum of the measurements of which is greater  cm, in the box with the sum of measurements less
cm, in the box with the sum of measurements less  see. The box can be tried to be laid arbitrarily crooked, askew, but you cannot knead.
see. The box can be tried to be laid arbitrarily crooked, askew, but you cannot knead.
Imagine that we have a lot of different rectangles (two-dimensional bricks) such that each brick has at least one side of an entire length. Of these bricks built a flat rectangular wall, without overlaps and holes, the bricks are not tilted. Prove that the resulting wall has at least one side of an entire length.

On the field dug round well. We have so many different infinitely long boards. Each board has its own width. And we completely closed the well with these boards so that there were no gaps left (the boards are not necessarily all parallel to each other). Prove that the sum of the width of the boards will always be not less than the diameter of the well.

Here you see a big cube with a cut piece, then a small cube standing in the corner.
In this post I have collected some of my favorite tasks, the solutions of which, it seems to me, cause this elusive dualism of feelings: “I understand - I don't understand”.
Circumference and ruler
Prove that using only one ruler you cannot find the center of a circle drawn on a plane (it is believed that the ruler has infinite length; it can connect any given points on the plane; there is no scale on the ruler, and nothing can be marked on it).
')
Decision Consider an inclined cone, the base of which is a certain circle
Consider an inclined cone, the base of which is a certain circle  . Since the cone is inclined, there is a plane that is not parallel to the base, which cuts out the second circle from the cone, let's call it
. Since the cone is inclined, there is a plane that is not parallel to the base, which cuts out the second circle from the cone, let's call it  .
.
Place a light bulb on top of the cone. This light bulb will cast a shadow of each straight line lying on the “upper” circle plane. on the plane of the "lower" circle
on the plane of the "lower" circle  . Moreover, the shadow of any straight line will also be straight. Note that this shadow is so cunning that despite the fact that it displays the "upper" circle
. Moreover, the shadow of any straight line will also be straight. Note that this shadow is so cunning that despite the fact that it displays the "upper" circle  in the "bottom"
in the "bottom"  , the shadow of the center of the "upper" circle does not fall into the center of the "lower".
, the shadow of the center of the "upper" circle does not fall into the center of the "lower".
Now let's imagine for a moment that there is such a wonderful algorithm that says how to find the center of any circle with one line. This algorithm, read a computer program, must consist of a sequence of actions of the type: draw an arbitrary line, draw a second arbitrary line, connect such and such an intersection point with such and such a point, then intersect the intersection point of this straight line and circle it with another certain point , and so on ... Note that if we use this miracle algorithm on the "upper" plane to find the center of the circle then the “shadow” of this algorithm will execute exactly the same commands on the “lower” plane. And since we assumed that our algorithm (a set of commands) finds the center of any circle, the “shadow” of the algorithm that executes the exact same commands is required to find the center of the lower circle. We immediately come to a contradiction, because, as we noted earlier, the shadow of the found center of the “upper” circle does not fall into the center of the “lower” one.
then the “shadow” of this algorithm will execute exactly the same commands on the “lower” plane. And since we assumed that our algorithm (a set of commands) finds the center of any circle, the “shadow” of the algorithm that executes the exact same commands is required to find the center of the lower circle. We immediately come to a contradiction, because, as we noted earlier, the shadow of the found center of the “upper” circle does not fall into the center of the “lower” one.
 Consider an inclined cone, the base of which is a certain circle
Consider an inclined cone, the base of which is a certain circle  . Since the cone is inclined, there is a plane that is not parallel to the base, which cuts out the second circle from the cone, let's call it
. Since the cone is inclined, there is a plane that is not parallel to the base, which cuts out the second circle from the cone, let's call it  .
.Place a light bulb on top of the cone. This light bulb will cast a shadow of each straight line lying on the “upper” circle plane.
 on the plane of the "lower" circle
on the plane of the "lower" circle  . Moreover, the shadow of any straight line will also be straight. Note that this shadow is so cunning that despite the fact that it displays the "upper" circle
. Moreover, the shadow of any straight line will also be straight. Note that this shadow is so cunning that despite the fact that it displays the "upper" circle  in the "bottom"
in the "bottom"  , the shadow of the center of the "upper" circle does not fall into the center of the "lower".
, the shadow of the center of the "upper" circle does not fall into the center of the "lower".Now let's imagine for a moment that there is such a wonderful algorithm that says how to find the center of any circle with one line. This algorithm, read a computer program, must consist of a sequence of actions of the type: draw an arbitrary line, draw a second arbitrary line, connect such and such an intersection point with such and such a point, then intersect the intersection point of this straight line and circle it with another certain point , and so on ... Note that if we use this miracle algorithm on the "upper" plane to find the center of the circle
 then the “shadow” of this algorithm will execute exactly the same commands on the “lower” plane. And since we assumed that our algorithm (a set of commands) finds the center of any circle, the “shadow” of the algorithm that executes the exact same commands is required to find the center of the lower circle. We immediately come to a contradiction, because, as we noted earlier, the shadow of the found center of the “upper” circle does not fall into the center of the “lower” one.
then the “shadow” of this algorithm will execute exactly the same commands on the “lower” plane. And since we assumed that our algorithm (a set of commands) finds the center of any circle, the “shadow” of the algorithm that executes the exact same commands is required to find the center of the lower circle. We immediately come to a contradiction, because, as we noted earlier, the shadow of the found center of the “upper” circle does not fall into the center of the “lower” one.Moscow metro task
In the Moscow metro there is a rule that prohibits bringing objects, the sum of the height, width and depth of which is greater
 see Let's agree that we are talking about rectangular boxes. Prove that it is impossible to deceive the system and completely thrust the box, the sum of the measurements of which is greater
see Let's agree that we are talking about rectangular boxes. Prove that it is impossible to deceive the system and completely thrust the box, the sum of the measurements of which is greater  cm, in the box with the sum of measurements less
cm, in the box with the sum of measurements less  see. The box can be tried to be laid arbitrarily crooked, askew, but you cannot knead.
see. The box can be tried to be laid arbitrarily crooked, askew, but you cannot knead.Decision
The decision was told to me by Hovhannes Khudaverdian .
For our proof, we need the concept - swelling over the body. Take an arbitrary body in space, its
- swelling over the body. Take an arbitrary body in space, its  -binding we call a set of points that are on the body or at a distance less than
-binding we call a set of points that are on the body or at a distance less than  From him. Let's say
From him. Let's say  -the inflation of a point in space will be a ball of radius
-the inflation of a point in space will be a ball of radius  , but
, but  -the expansion of the segment will be the body, like a sausage.
-the expansion of the segment will be the body, like a sausage.
Now we take our parallelepiped (box plus its internal part) with dimensions ,
,  and
and  and volume respectively
and volume respectively  . Try to calculate the volume
. Try to calculate the volume  her
her  - swelling. In it
- swelling. In it  - airflow includes:
- airflow includes:
We get that volume -box drawer sweep will equal
-box drawer sweep will equal

Let now in a box with the sizes of the parties ,
,  and
and  is the second box
is the second box  ,
,  and
and  . It is clear that whatever number
. It is clear that whatever number  we didn't take
we didn't take  -inflation of the inner box will lie in
-inflation of the inner box will lie in  -blowdown external box, so its volume will be less:
-blowdown external box, so its volume will be less:

Substitute the inequality for the expression for volumes, reduce the same terms and divide everything by :
:
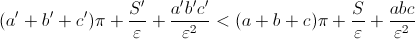
Note that the last inequality must be satisfied for any , for both small and large. Therefore, we can always go to the limit
, for both small and large. Therefore, we can always go to the limit  , we get:
, we get:

So we proved that if one box is in the second, then the sum of its dimensions cannot be greater.
For our proof, we need the concept
 - swelling over the body. Take an arbitrary body in space, its
- swelling over the body. Take an arbitrary body in space, its  -binding we call a set of points that are on the body or at a distance less than
-binding we call a set of points that are on the body or at a distance less than  From him. Let's say
From him. Let's say  -the inflation of a point in space will be a ball of radius
-the inflation of a point in space will be a ball of radius  , but
, but  -the expansion of the segment will be the body, like a sausage.
-the expansion of the segment will be the body, like a sausage.Now we take our parallelepiped (box plus its internal part) with dimensions
 ,
,  and
and  and volume respectively
and volume respectively  . Try to calculate the volume
. Try to calculate the volume  her
her  - swelling. In it
- swelling. In it  - airflow includes:
- airflow includes:- box itself volume
 ;
; - growths over the edges of the box. If we denote the total surface area of the box for
 then the volume of these growths will be
then the volume of these growths will be  .
. - growths over the edges of the box. Each such growth is a quarter of a cylinder with a base radius
 . Since in a box of four edges of length
. Since in a box of four edges of length  ,
,  and
and  , then growths with every four of the same ribs can be combined into one single cylinder. The total volume of the resulting three cylinders will be
, then growths with every four of the same ribs can be combined into one single cylinder. The total volume of the resulting three cylinders will be  ;
; - growths above the tops of the box. Each such growth is an eighth part of a ball of radius.
 . Therefore, from the growths over all eight of the top of the box, you can collect one whole ball of radius
. Therefore, from the growths over all eight of the top of the box, you can collect one whole ball of radius  i.e. volume
i.e. volume  .
.
We get that volume
 -box drawer sweep will equal
-box drawer sweep will equal
Let now in a box with the sizes of the parties
 ,
,  and
and  is the second box
is the second box  ,
,  and
and  . It is clear that whatever number
. It is clear that whatever number  we didn't take
we didn't take  -inflation of the inner box will lie in
-inflation of the inner box will lie in  -blowdown external box, so its volume will be less:
-blowdown external box, so its volume will be less:
Substitute the inequality for the expression for volumes, reduce the same terms and divide everything by
 :
: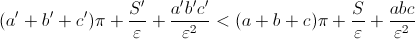
Note that the last inequality must be satisfied for any
 , for both small and large. Therefore, we can always go to the limit
, for both small and large. Therefore, we can always go to the limit  , we get:
, we get:
So we proved that if one box is in the second, then the sum of its dimensions cannot be greater.
Brick wall
Imagine that we have a lot of different rectangles (two-dimensional bricks) such that each brick has at least one side of an entire length. Of these bricks built a flat rectangular wall, without overlaps and holes, the bricks are not tilted. Prove that the resulting wall has at least one side of an entire length.

Decision
Before solving a problem, let's recall one remarkable property of the function  : its integral over any segment whose length is a multiple of
: its integral over any segment whose length is a multiple of  , is equal to zero. Really
, is equal to zero. Really

Moreover, if the integral of the function from zero to some number
from zero to some number  is zero, then we can safely assume that the number
is zero, then we can safely assume that the number  multiple
multiple  .
.
Similarly, it is shown that for the function “compressed” horizontally , the integral over any segment whose length is a multiple of one (integer) is equal to zero:
, the integral over any segment whose length is a multiple of one (integer) is equal to zero:
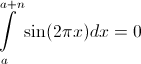
Now consider the function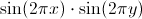 (we will place the origin of coordinates in the lower left corner of the wall). This function has such a wonderful property that its integral over any brick on the wall is zero:
(we will place the origin of coordinates in the lower left corner of the wall). This function has such a wonderful property that its integral over any brick on the wall is zero:

Indeed, in fact, one of the integrals on the right is taken over a segment of length an integer, and therefore is equal to zero.
We see that the integral of our wonderful function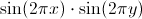 by any of the bricks on the wall is zero, so this integral is zero and on the entire wall built by these bricks, since it is simply the sum of the integrals over each of the bricks. We get:
by any of the bricks on the wall is zero, so this integral is zero and on the entire wall built by these bricks, since it is simply the sum of the integrals over each of the bricks. We get:

Means or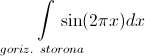 , or
, or 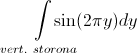 must be zero. From which it immediately follows that either the horizontal or the vertical side of the wall has an entire length.
must be zero. From which it immediately follows that either the horizontal or the vertical side of the wall has an entire length.
( upd: as the readers tell me, the task has at least 14 solutions )
 : its integral over any segment whose length is a multiple of
: its integral over any segment whose length is a multiple of  , is equal to zero. Really
, is equal to zero. Really
Moreover, if the integral of the function
 from zero to some number
from zero to some number  is zero, then we can safely assume that the number
is zero, then we can safely assume that the number  multiple
multiple  .
.Similarly, it is shown that for the function “compressed” horizontally
 , the integral over any segment whose length is a multiple of one (integer) is equal to zero:
, the integral over any segment whose length is a multiple of one (integer) is equal to zero: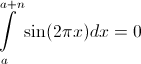
Now consider the function
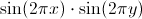 (we will place the origin of coordinates in the lower left corner of the wall). This function has such a wonderful property that its integral over any brick on the wall is zero:
(we will place the origin of coordinates in the lower left corner of the wall). This function has such a wonderful property that its integral over any brick on the wall is zero:
Indeed, in fact, one of the integrals on the right is taken over a segment of length an integer, and therefore is equal to zero.
We see that the integral of our wonderful function
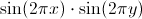 by any of the bricks on the wall is zero, so this integral is zero and on the entire wall built by these bricks, since it is simply the sum of the integrals over each of the bricks. We get:
by any of the bricks on the wall is zero, so this integral is zero and on the entire wall built by these bricks, since it is simply the sum of the integrals over each of the bricks. We get:
Means or
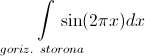 , or
, or 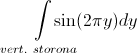 must be zero. From which it immediately follows that either the horizontal or the vertical side of the wall has an entire length.
must be zero. From which it immediately follows that either the horizontal or the vertical side of the wall has an entire length.( upd: as the readers tell me, the task has at least 14 solutions )
Problem about the well
On the field dug round well. We have so many different infinitely long boards. Each board has its own width. And we completely closed the well with these boards so that there were no gaps left (the boards are not necessarily all parallel to each other). Prove that the sum of the width of the boards will always be not less than the diameter of the well.
Decision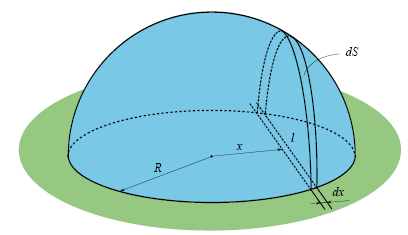 The decision, if I am not mistaken, belongs to Alexander Karabegov .
The decision, if I am not mistaken, belongs to Alexander Karabegov .
Let's cover the well with a hemisphere, as shown in the figure, and in the well we will install a huge searchlight, which shines with parallel vertical rays upwards. And consider a very, very thin board, width which lies on the well.
which lies on the well.
Note that the farther the distance of the board from the center of the well, the less becomes the length which is occupied by the board directly above the well, but at the same time the angle of the shadow from this board on the hemisphere becomes steeper. It turns out that these two processes compensate each other, and the area of the shadow
which is occupied by the board directly above the well, but at the same time the angle of the shadow from this board on the hemisphere becomes steeper. It turns out that these two processes compensate each other, and the area of the shadow  does not depend on the distance of the board from the center of the well. Indeed, the length of the board above the well
does not depend on the distance of the board from the center of the well. Indeed, the length of the board above the well 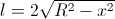 and the tangent of the angle of the shadow is
and the tangent of the angle of the shadow is  . We get the formula for the area
. We get the formula for the area 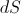 the shadow of the board, which is equal to the length of the shadow multiplied by its width:
the shadow of the board, which is equal to the length of the shadow multiplied by its width:
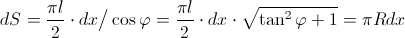
We see that, indeed, wherever a well is located, a very thin board with a width , square
, square 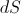 its shadow on the hemisphere will always equal
its shadow on the hemisphere will always equal  that is, it will depend only on the width of the board
that is, it will depend only on the width of the board  . This property of “independence” is also fulfilled for boards of any width, because they can be represented as a multitude of thin boards fastened together. As a result, we get a remarkable result: if the width of the board above the well is
. This property of “independence” is also fulfilled for boards of any width, because they can be represented as a multitude of thin boards fastened together. As a result, we get a remarkable result: if the width of the board above the well is 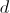 then the area of her shadow
then the area of her shadow 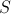 equals
equals 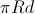 .
.
Now let a set of boards of width completely close our well. Some of the boards can, of course, not be as wide as they are above the well. Therefore, the area of the shadow of each of the boards
completely close our well. Some of the boards can, of course, not be as wide as they are above the well. Therefore, the area of the shadow of each of the boards 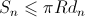 . Different boards can overlap each other, so the total shadow area
. Different boards can overlap each other, so the total shadow area
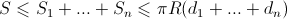
But since the boards cover the well without gaps, their common shadow fills the entire hemisphere, and therefore has an area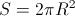 . As a result, we obtain that
. As a result, we obtain that
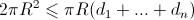

Q.E.D.
 The decision, if I am not mistaken, belongs to Alexander Karabegov .
The decision, if I am not mistaken, belongs to Alexander Karabegov .Let's cover the well with a hemisphere, as shown in the figure, and in the well we will install a huge searchlight, which shines with parallel vertical rays upwards. And consider a very, very thin board, width
 which lies on the well.
which lies on the well.Note that the farther the distance of the board from the center of the well, the less becomes the length
 which is occupied by the board directly above the well, but at the same time the angle of the shadow from this board on the hemisphere becomes steeper. It turns out that these two processes compensate each other, and the area of the shadow
which is occupied by the board directly above the well, but at the same time the angle of the shadow from this board on the hemisphere becomes steeper. It turns out that these two processes compensate each other, and the area of the shadow 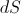 does not depend on the distance of the board from the center of the well. Indeed, the length of the board above the well
does not depend on the distance of the board from the center of the well. Indeed, the length of the board above the well 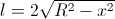 and the tangent of the angle of the shadow is
and the tangent of the angle of the shadow is  . We get the formula for the area
. We get the formula for the area 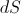 the shadow of the board, which is equal to the length of the shadow multiplied by its width:
the shadow of the board, which is equal to the length of the shadow multiplied by its width: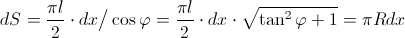
We see that, indeed, wherever a well is located, a very thin board with a width
 , square
, square 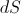 its shadow on the hemisphere will always equal
its shadow on the hemisphere will always equal  that is, it will depend only on the width of the board
that is, it will depend only on the width of the board  . This property of “independence” is also fulfilled for boards of any width, because they can be represented as a multitude of thin boards fastened together. As a result, we get a remarkable result: if the width of the board above the well is
. This property of “independence” is also fulfilled for boards of any width, because they can be represented as a multitude of thin boards fastened together. As a result, we get a remarkable result: if the width of the board above the well is 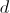 then the area of her shadow
then the area of her shadow 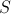 equals
equals 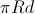 .
.Now let a set of boards of width
 completely close our well. Some of the boards can, of course, not be as wide as they are above the well. Therefore, the area of the shadow of each of the boards
completely close our well. Some of the boards can, of course, not be as wide as they are above the well. Therefore, the area of the shadow of each of the boards 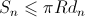 . Different boards can overlap each other, so the total shadow area
. Different boards can overlap each other, so the total shadow area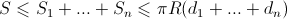
But since the boards cover the well without gaps, their common shadow fills the entire hemisphere, and therefore has an area
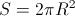 . As a result, we obtain that
. As a result, we obtain that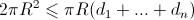

Q.E.D.
Source: https://habr.com/ru/post/184510/
All Articles