Elliptical Spirograph
In childhood I had a toy called spirograph. This is such a plastic sheet with a round hole inside, and toothed gears were attached to it, also with holes, but small. You put a pen in the hole, a gear in a circle and roll . The result is beautiful lace patterns that you can’t draw with your hands.
When I became older, I wanted to bring the same patterns already on the computer screen. For a long time I thought how to do it, according to what formula to draw. In the meantime, I thought this formula was derived without me, and even put it on Wikipedia - I don’t want to draw. The basic idea of the conclusion there is that a small circle travels large without slipping, and, therefore, the distance traveled by a point from a small circle must be equal to the corresponding distance on a large circle.
However, taken the fortress no longer beckon. Now it’s natural to summarize the task - for example, to make a small circle not go inside a circle, but rather more complicated, say, an ellipse.
')
But then it turns out sharply that the conclusion from Wikipedia is sharpened just under the circle. And for other figures, we immediately come across three obstacles.
First, the circle is a simple figure and it is very easy to calculate its length: it multiplied the angle of rotation by the radius, and it was done. But the length of an ellipse, not to mention something more complicated, is an integral of a special kind, to which even its own name is assigned “elliptic function”. And this integral is not perceptible - that is, it is not expressed in elementary functions. And counting the length of an ellipse through derivatives, and taking into account that there is a parametric formula there, pleasure is small. That is, it is possible to program, of course, but the calculations are performed very, very long.
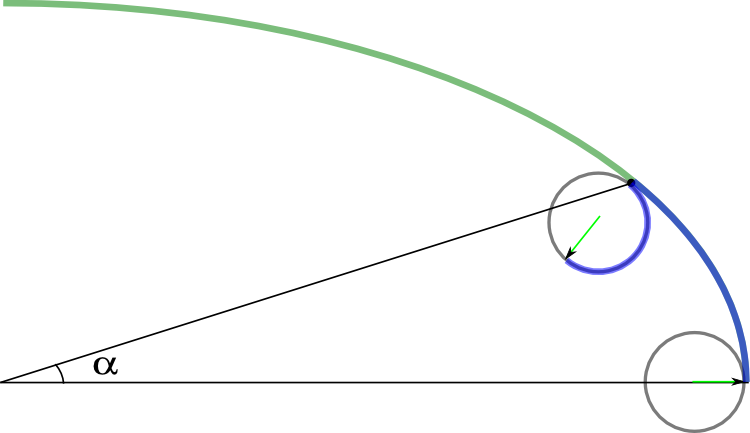
Secondly, the circle is a figure of constant curvature. Therefore, the line between the point of tangency of the circles and the center of the large circle always also passes through the small circle at the same time, which simplifies the derivation of formulas. In the case of an ellipse (and any other curve with varying curvature), these points move apart in different directions like a cow on ice. Here is an illustration.
On the third problem will be discussed later.
But the mind overcomes all obstacles. Or almost everything. If we take from Wikipedia the main idea of equality of the distance traveled and the second idea - to consider the location of the hole in the gear as the sum of the location of the center of the small circle relative to the large one and the location of the hole relatively small circle, then after a certain amount of trial and error we can come up with an algorithm for drawing.
So look again at the illustration above. The center of the Cartesian and polar coordinates (we will have to use both) is in one place — the middle of the main ellipse; we measure the polar angles counterclockwise from the x axis. On a small circle, a green arrow was drawn especially for beauty. Initially, at an angle of 0, the small circle stands so that this arrow is at an angle of 0, and its tangency point with a large circle is on the x axis.
Now the wheel was turned so that the point of contact moved to a point that is at an angle α, when viewed from the origin. During this time, the end of the arrow passed a certain path, and this path is equal to the corresponding path on the ellipse (in the figure both are marked in blue).
Let's get a little closer to the scene.
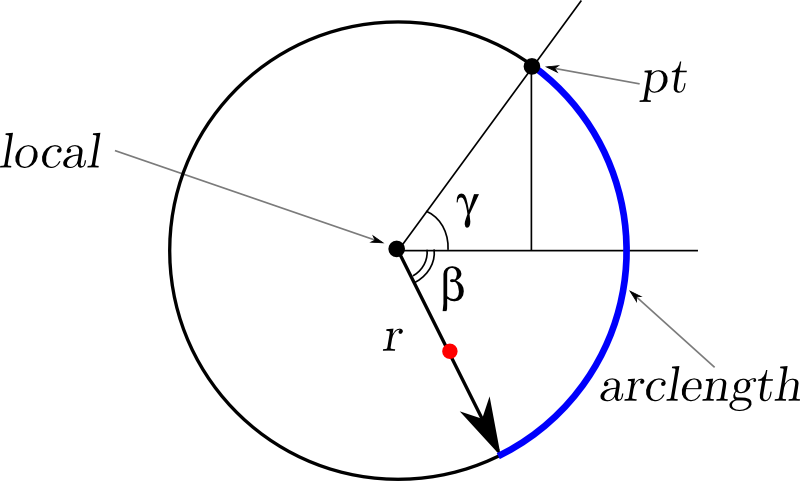
Here we see the same point of contact (marked as pt), the arrow on the wheel (drawn in bold), the path traversed by the end of this arrow (highlighted in blue), and at the same time a hole in the wheel (red dot). local is the center of the wheel, at this point the center of the local coordinate system will be placed, with which we will calculate the position of the hole.
So, the point pt is visible from the center of the ellipse at an angle α. It is easy to find the coordinates of this point - as the intersection of an ellipse and the corresponding line. Now it would be nice to know the coordinates of the center of the wheel, but for this we need to know the angle γ - the direction from the center of the wheel to the touch point. ABOUT! - the key word "touch". At the tangency point of the curves, a common tangent can be drawn to them, and the angle we need will be perpendicular to the angle of this tangent. The tangent of the tangent angle is the derivative of the ellipse at a point. It remains only to simply calculate this derivative.
Of course, you can take the parametric equation of an ellipse and get a derivative formula from it. But it is terribly inconvenient - the parameter does not correspond in any way with any value known to us. And if we replace the ellipse with something else?
Physicists joke that God has an important advantage that can integrate live, directly on physical bodies. This is the method we will use.
What is a derivative? If in a simple way, in a collective farm, excluding the limiting transition, this is the ratio of a change in the value of a function to a change in the value of a variable. Since we program on a computer, we don’t have any infinities implied by the limiting transition, our world is discrete, and for us this formula is quite suitable. Therefore, we only need to memorize the previous point and calculate the ratio (Ypt-Yprev) / (Xpt-Xprev). The more often we take the points, the more accurate our calculations will be and in the end, no one can distinguish them from a real derivative.
Well, then simply - we find the angle γ and the coordinates of the center of the wheel on it.
How now to find the coordinates of the holes in the local coordinates? All that is necessary for this to know is at what angle β the wheel was turned. You cannot calculate it directly, but it is equal to the angle between the touch point and the end of the arrow, from which the angle γ already known to us was subtracted (see picture). It is necessary only to remember to take the result with the opposite sign, because our wheel turns clockwise, and the angles are measured against the hour.
How to find a large angle? Not so difficult - you just need to divide the length of the blue arc by the radius of the wheel. And the length of the blue arc is equal to the corresponding part of the arc of the ellipse.
Aha-aha, this is where terrible elliptic functions are waiting for us. But we will unscrew as well as with the derivative - we will replace the length of the curve with the length of the polyline, which consists of short straight lines between the current point and the previous one.
Well, the rest is easy - we find the coordinates of the red point in the local coordinate system and recalculate them into the global one.
Now about the third problem. In Wikipedia, the radii of the large and small circle are set and they predict that if their attitude is rational, then the curve will necessarily close (and why do we need open curves? They are not beautiful). We can also do this, but it is useless - the length of the ellipse is expressed as an irrational number, we have no radius, and the curve is not likely to close.
We will do it a little differently: we will set the number of times the wheel will move in an ellipse, and how many times this time it should turn itself. According to this data, we calculate what radius the wheel should have in order for the curve to close. Here all the same equality of ways will help us.
Now, after long calculations, we will finally be able to enjoy the artistic result. See how cute:

The yellow circle in the picture is the wheel, the outer black ellipse is the one in which we roll, the yellow ellipse is the way to the middle of the wheel.
By the way, the resulting algorithm is completely independent of any properties of the ellipse, so the outer curve can be changed as you please, as long as it remains closed. You can even take ... square. The result is in the following figure. He is not so pleased with the eye, but also nothing. Then it will be possible to cut off all unnecessary in Photoshop.

Beautiful, what to say. But since this is not a promotional post, I just can not ignore an important drawback. All of the above works if the curve is smooth enough and the wheel is small. If the wheel is comparable in magnitude to the curve itself, then the above conclusion is no longer valid. Doubtful jags appear on the graph, since when calculating by the algorithm, it turns out that the wheel in some places stands in such a way that it touches the outer curve only at one point, and its neighboring points turn out to be sticking out of the curve. Of course, on a physical spirograph this will not work, but how to fix it is not yet known to modern science. If anyone has any ideas - please pop up.
And finally, for those who, for their flowery prose, prefer the harsh speech of algorithms, the text of the program. It is written in Asymptote , an excellent computer graphics programming tool.
When I became older, I wanted to bring the same patterns already on the computer screen. For a long time I thought how to do it, according to what formula to draw. In the meantime, I thought this formula was derived without me, and even put it on Wikipedia - I don’t want to draw. The basic idea of the conclusion there is that a small circle travels large without slipping, and, therefore, the distance traveled by a point from a small circle must be equal to the corresponding distance on a large circle.
However, taken the fortress no longer beckon. Now it’s natural to summarize the task - for example, to make a small circle not go inside a circle, but rather more complicated, say, an ellipse.
')
But then it turns out sharply that the conclusion from Wikipedia is sharpened just under the circle. And for other figures, we immediately come across three obstacles.
First, the circle is a simple figure and it is very easy to calculate its length: it multiplied the angle of rotation by the radius, and it was done. But the length of an ellipse, not to mention something more complicated, is an integral of a special kind, to which even its own name is assigned “elliptic function”. And this integral is not perceptible - that is, it is not expressed in elementary functions. And counting the length of an ellipse through derivatives, and taking into account that there is a parametric formula there, pleasure is small. That is, it is possible to program, of course, but the calculations are performed very, very long.
Secondly, the circle is a figure of constant curvature. Therefore, the line between the point of tangency of the circles and the center of the large circle always also passes through the small circle at the same time, which simplifies the derivation of formulas. In the case of an ellipse (and any other curve with varying curvature), these points move apart in different directions like a cow on ice. Here is an illustration.

On the third problem will be discussed later.
But the mind overcomes all obstacles. Or almost everything. If we take from Wikipedia the main idea of equality of the distance traveled and the second idea - to consider the location of the hole in the gear as the sum of the location of the center of the small circle relative to the large one and the location of the hole relatively small circle, then after a certain amount of trial and error we can come up with an algorithm for drawing.
So look again at the illustration above. The center of the Cartesian and polar coordinates (we will have to use both) is in one place — the middle of the main ellipse; we measure the polar angles counterclockwise from the x axis. On a small circle, a green arrow was drawn especially for beauty. Initially, at an angle of 0, the small circle stands so that this arrow is at an angle of 0, and its tangency point with a large circle is on the x axis.
Now the wheel was turned so that the point of contact moved to a point that is at an angle α, when viewed from the origin. During this time, the end of the arrow passed a certain path, and this path is equal to the corresponding path on the ellipse (in the figure both are marked in blue).
Let's get a little closer to the scene.

Here we see the same point of contact (marked as pt), the arrow on the wheel (drawn in bold), the path traversed by the end of this arrow (highlighted in blue), and at the same time a hole in the wheel (red dot). local is the center of the wheel, at this point the center of the local coordinate system will be placed, with which we will calculate the position of the hole.
So, the point pt is visible from the center of the ellipse at an angle α. It is easy to find the coordinates of this point - as the intersection of an ellipse and the corresponding line. Now it would be nice to know the coordinates of the center of the wheel, but for this we need to know the angle γ - the direction from the center of the wheel to the touch point. ABOUT! - the key word "touch". At the tangency point of the curves, a common tangent can be drawn to them, and the angle we need will be perpendicular to the angle of this tangent. The tangent of the tangent angle is the derivative of the ellipse at a point. It remains only to simply calculate this derivative.
Of course, you can take the parametric equation of an ellipse and get a derivative formula from it. But it is terribly inconvenient - the parameter does not correspond in any way with any value known to us. And if we replace the ellipse with something else?
Physicists joke that God has an important advantage that can integrate live, directly on physical bodies. This is the method we will use.
What is a derivative? If in a simple way, in a collective farm, excluding the limiting transition, this is the ratio of a change in the value of a function to a change in the value of a variable. Since we program on a computer, we don’t have any infinities implied by the limiting transition, our world is discrete, and for us this formula is quite suitable. Therefore, we only need to memorize the previous point and calculate the ratio (Ypt-Yprev) / (Xpt-Xprev). The more often we take the points, the more accurate our calculations will be and in the end, no one can distinguish them from a real derivative.
Well, then simply - we find the angle γ and the coordinates of the center of the wheel on it.
How now to find the coordinates of the holes in the local coordinates? All that is necessary for this to know is at what angle β the wheel was turned. You cannot calculate it directly, but it is equal to the angle between the touch point and the end of the arrow, from which the angle γ already known to us was subtracted (see picture). It is necessary only to remember to take the result with the opposite sign, because our wheel turns clockwise, and the angles are measured against the hour.
How to find a large angle? Not so difficult - you just need to divide the length of the blue arc by the radius of the wheel. And the length of the blue arc is equal to the corresponding part of the arc of the ellipse.
Aha-aha, this is where terrible elliptic functions are waiting for us. But we will unscrew as well as with the derivative - we will replace the length of the curve with the length of the polyline, which consists of short straight lines between the current point and the previous one.
Well, the rest is easy - we find the coordinates of the red point in the local coordinate system and recalculate them into the global one.
Now about the third problem. In Wikipedia, the radii of the large and small circle are set and they predict that if their attitude is rational, then the curve will necessarily close (and why do we need open curves? They are not beautiful). We can also do this, but it is useless - the length of the ellipse is expressed as an irrational number, we have no radius, and the curve is not likely to close.
We will do it a little differently: we will set the number of times the wheel will move in an ellipse, and how many times this time it should turn itself. According to this data, we calculate what radius the wheel should have in order for the curve to close. Here all the same equality of ways will help us.
Now, after long calculations, we will finally be able to enjoy the artistic result. See how cute:

The yellow circle in the picture is the wheel, the outer black ellipse is the one in which we roll, the yellow ellipse is the way to the middle of the wheel.
By the way, the resulting algorithm is completely independent of any properties of the ellipse, so the outer curve can be changed as you please, as long as it remains closed. You can even take ... square. The result is in the following figure. He is not so pleased with the eye, but also nothing. Then it will be possible to cut off all unnecessary in Photoshop.

Beautiful, what to say. But since this is not a promotional post, I just can not ignore an important drawback. All of the above works if the curve is smooth enough and the wheel is small. If the wheel is comparable in magnitude to the curve itself, then the above conclusion is no longer valid. Doubtful jags appear on the graph, since when calculating by the algorithm, it turns out that the wheel in some places stands in such a way that it touches the outer curve only at one point, and its neighboring points turn out to be sticking out of the curve. Of course, on a physical spirograph this will not work, but how to fix it is not yet known to modern science. If anyone has any ideas - please pop up.
And finally, for those who, for their flowery prose, prefer the harsh speech of algorithms, the text of the program. It is written in Asymptote , an excellent computer graphics programming tool.
// , path base = scale(3,2)*unitcircle; // - ; , //path base = unitcircle; // - // path base = (-3,3)--(3,3)--(3,-3)--(-3,-3)--cycle; // // (0 - , -1 - , +1 - ) real p = 0.7; import graph; size(600, 600); // //xaxis(ticks=Ticks); //yaxis(ticks=Ticks); // int m = 9; // int n = 29; // , real r = arclength(base)*m/2/pi/n; real hole = r*p; draw(base); //////////////////////////////////////////////// // , phase - real revolution(real phase) { pair prev = (500,500); real arclen = 0; real beta; real gamma; for (real alpha = 0; alpha<=2pi; alpha=alpha+0.005) { // real[][] isect = intersections(base, (0,0)--(500*cos(alpha), 500*sin(alpha))); pair pt = point(base, isect[0][0]); if (prev==(500,500)) { gamma = 0; } else { // arclen += length(pt-prev); // , pair deriv = pt - prev; // real g = atan2(deriv.y, deriv.x); // gamma = g - pi/2; } beta = gamma - arclen/r + phase; // pair local = hole*( cos(beta), sin(beta) ); // pair center = pt - r*( cos(gamma), sin(gamma) ); pair spiro = center + local; draw(center, green); draw(spiro, blue); // - prev = pt; } return beta; } //////////////////////////////////// // - real[][] isect = intersections(base, (0,0)--(100, 0)); pair first_point = point(base,isect[0][0]); draw(shift(first_point.xr,0)*scale(r)*unitcircle, yellow); // , real phase = 0; for (int rev=0; rev<m; rev=rev+1) { phase = revolution(phase); } Source: https://habr.com/ru/post/184466/
All Articles