I'm doing my quadrocopter. Part 1. Dynamics equations

Table of contents

1. Equations of dynamics

Introduction

A long time ago I wrote the following comment: Everything.
After such news I sit down to do my quadrocopter. And then they do everything, but I do not. No, but what?
Always wanted me to have some kind of flying thing. There were 2 radio-controlled helicopters. But it ended badly.
I decided to do my quadrocopter. How it will end - we'll see. I will not use any ready-made flight controllers, I will program everything myself. And I will try to describe this process in a series of articles. Now I present to you the first part. It will briefly show which dynamic equations are hidden inside the quadcopter.
So let's go.
')

1. Derivation of equations of motion

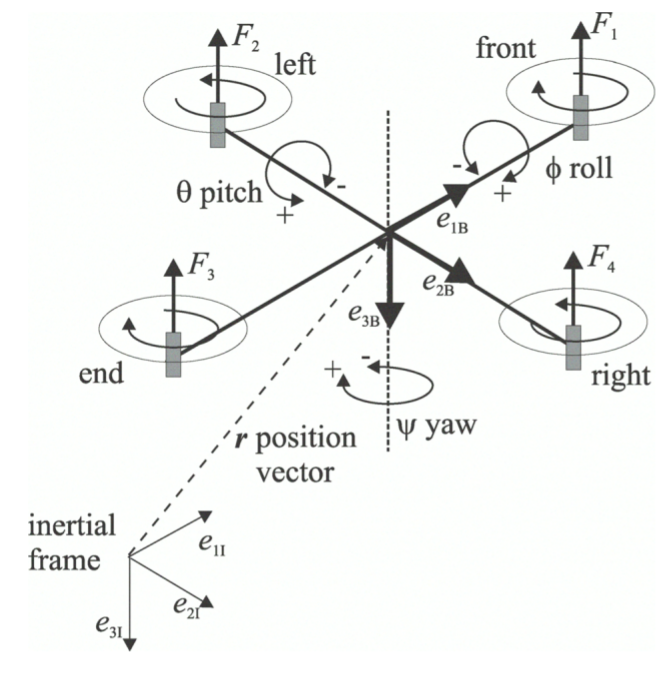
The quadcopter orientation in space is defined by three angles: yaw - ψ , pitch - θ , roll - φ .
Together they make up a vector
.
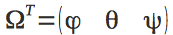The position of the device in the inertial reference system is set by the radius vector
.
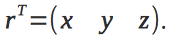The transition matrix from the quadrocopter's coordinate system to the inertial coordinate system is as follows

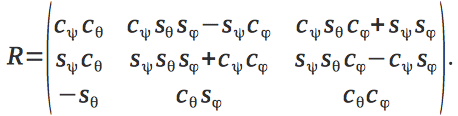
The thrust produced by each of the four engines is equal to

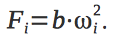
Here ω _i is the angular velocity of the engine, and b is the coefficient of proportionality.
Now we can write a differential equation describing quadroopter acceleration along the vertical axis.

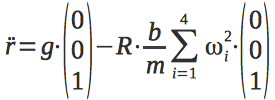
Immediately write the second differential equation

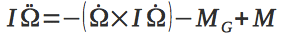
Here I is the inertia matrix, M is the torque applied to the quadcopter, M _G is the gyroscopic moment.
Vector M is defined as follows:

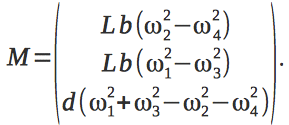
Here d is the drag coefficient, L is the shoulder length.
The gyroscopic moments caused by the rotation of an object with rotating rotors of the engines are recorded as follows:


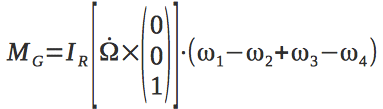
We will introduce 4 control signals that will drive a quadrocopter:





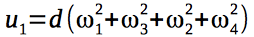
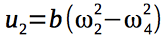
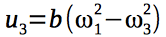
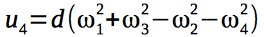
The gyroscopic moments acting on the quadrocopter depend on the angular velocities of the rotors of the engines and, therefore, on the control vector


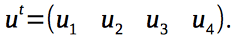
We write the system of equations describing our system.


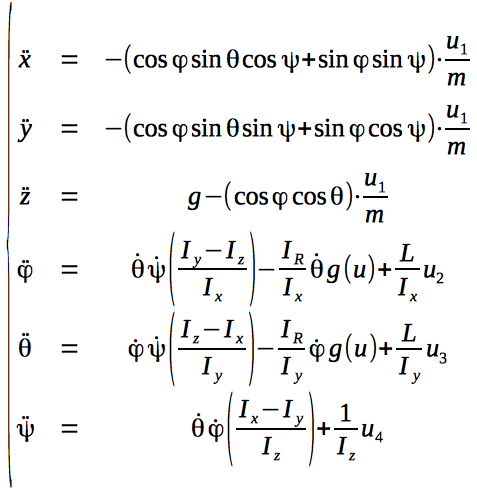
And now we will transform the system in such a way that there are no second derivatives.


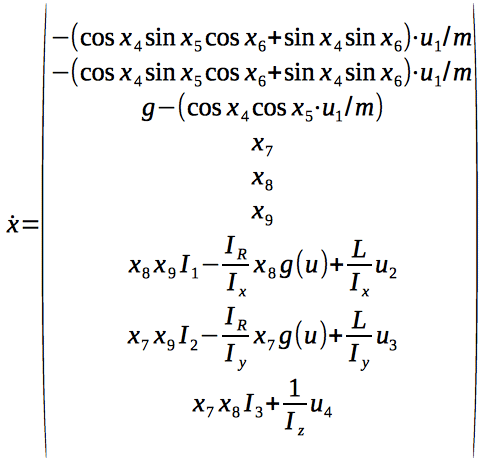
This system of 9 equations describes the dynamics of the system.

Conclusion

The post has turned out a little ugly.
Can you please tell me the online formula editor? And then these look absolutely disgusting.

Questions and suggestions are welcome!