Tricky quaternions

Guess the riddle: sits in four dimensions and turns up complex numbers?

Hint: This is a vector with a scalar. And the real matrix. And he came up with Hamilton.
')
Did not help? Well, you, it's elementary! This is a quaternion! Quaternions are used to record rotations in robotics, game engines, modeling software, and in general everywhere where problems with Euler angles or matrices are not needed. If you are frightened by the confusion above with different views of the quaternion, then you can be calm. Quaternions are very easy to use and their internal structure may be needed only in very rare cases where fine optimization is needed. The rest of the time, using quaternions, you can turn anything and anything, and it will interpolate smoothly and beautifully without hinged locks .

What is a quaternion? It is easiest to understand it if it is divided into two parts: a vector and rotation around it. Imagine that you are inside a sphere. You can reach out and touch the inside of the sphere. This will be a vector. Now, if you rotate the sphere by rotating the brush, you will get the second component of the quaternion. Quaternion is the final rotation, which is obtained from the initial position.

Quaternion has a cunning internal structure. It can be written with the help of four numbers: x, y, z for the vector and w for the rotation. The difficulty lies in the fact that in addition to them there are still three imaginary units, such that: i ² = j ² = k ² = ijk = −1. The whole entry looks like this: q = w + x * i + y * j + z * k

Because of the units, the addition-multiplication of quaternions by hand is rather dreary, but, fortunately, they are not particularly important in programming. All operations are usually performed on quaternions as a whole, and only those four numbers are rarely used. In addition, many libraries have special constructors that allow you to get quaternion from more understandable structures, for example, Quaternion.Euler in Unity3d or Quaternion.CreateFromYawPitchRoll in XNA.

In working with quaternions, they most often have to multiply them. This is a very useful operation, since multiplying one quaternion by another results in the first rotation, turned on the second. It is important to remember that multiplication of quaternions is noncommutative, which means that the order of the operands is important. That is, q ₁ * q ₂ is not the same as q ₂ * q ₁ . In the picture below you can see the difference. Left: Quaternion.Euler (60, 0, 60) * Quaternion.Euler (0, 60, 0), right: Quaternion.Euler (0, 60, 0) * Quaternion.Euler (60, 0, 60). The colored lines show the paths of the local axes of each airplane.



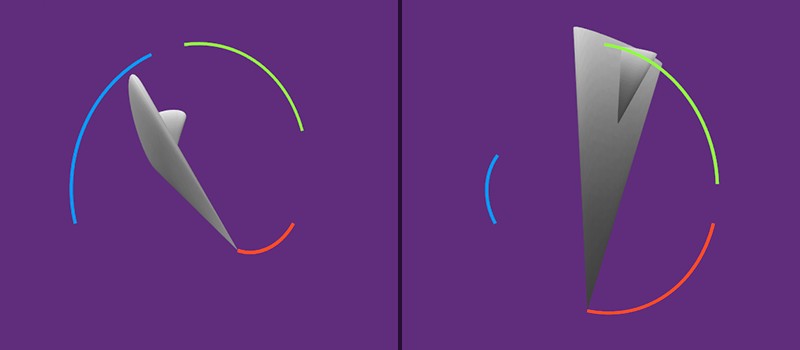
In practice, working with quaternions looks like this:

var rightTurn = Quaternion.Euler(0, 90, 0); //     car.rotation = car.rotation*rightTurn; //  

In the example above, the car type is turning to the right in local coordinates. If the car travels on an inclined plane, or even upside down, then it will still correctly turn to the right place. The rightTurn variable can be used any number of times, like this, for example, a 360-degree rotation looks like:

 car.rotation = car.rotation*rightTurn*rightTurn*rightTurn*rightTurn; 

By default, the quaternion uses global coordinate axes to count the rotation. When one quaternion is multiplied by another quaternion, then for the second quaternion the first quaternion becomes the reference point.

If you suddenly wanted to model the movement on a variety of convex surfaces like in Super Mario Galaxy using Euler angles, then you would have to puzzle for a long time. This is because they were invented to indicate the specific orientation of the object in space, and not for animation. With quaternions, everything is much simpler, and they interpolate remarkably along the shortest paths, while Euler angles start to wriggle because of the hierarchy of turns and often get stuck in the hinged lock, about which I wrote in this article . On the animation below you can see how much their spherical interpolation differs. Quaternions on the left, Euler angles on the right.



If you are still interested in how quaternions look inside, then you can look at the table below.

w	x	y	z	Rotation
one	0	0	0	no rotation
0	one	0	0	180 ° around the x axis
sqrt (0.5)	sqrt (0.5)	0	0	90 ° around the x axis
sqrt (0.5)	-sqrt (0.5)	0	0	-90 ° around the x-axis

The values ​​in the table are obtained from the following formula:

 [w, x, y, z] = [cos(alpha/2), sin(alpha/2)*vx, sin(alpha/2)*vy, sin(alpha/2)*vz] 

Where alpha is the angle of rotation, and vx, vy, vz is the vector of the axis of rotation.

The result of the addition of quaternions is an intermediate rotation. The addition of quaternions is elementary, it is enough just to add their components. Take, for example, q ₁ = 1 + 0i + 0j + 0k (zero rotation from the table above) and q ₂ = 0 + 1i + 0j + 0k (180 ° around the X axis). Their sum is q ₃ = 1 + 1i + 0j + 0k, that is, 90 ° around the X axis. Unfortunately, in Unity3d the addition operator is not implemented for quaternions.

If you want to learn more about quaternions, then I advise you to start with the English Wikipedia . You can also delve into Wolfram | Alpha , it gives tons of passing information and generally can do a lot. You can also look at the difference between Euler angles and quaternions in the interactive demonstration on the links below.


WebGL | Windows | Linux | Mac | Sources on GitHub
Use the mouse to rotate the scene, AD, WS and QE - rotate around the axes, Esc - exit, the other buttons are indicated on the screen.
For Linux users: Make the Quaternions file executable with “chmod + x Quaternions” and run.