Analyzing numeric sequences

Sometimes, if you deal with numerical sequences or binary data, there is a desire to “touch” them, to understand how they are arranged, whether they are subject to compression, if they are encrypted, then how qualitatively. If we are talking about pseudo-random number generators, I want to know how pseudo and how random they are.
In fact, what can you think of, well ... expectation, calculate the variance, or which histogram to build ...
Now we will consider a method that allows you to take a kind of fingerprints from numerical sequences.

• Suppose we have a generator of integers that can produce a lot of them (10 000 000 in our case).
• Choose the size of the print, which we will now “roll”, let Sz = 1024
• Select and reset the memory for an integral two-dimensional square matrix of size Sz: Hists [Sz] [Sz]
• Subtract from the generator number and for each of them (Val) arrange cycle
  

  for (size_t ix = 1; ix <= Sz; ix++) { size_t histix = Val % ix; Hists[ix-1][histix] ++; } 

  Those. we build a histogram of residuals from dividing the input values ​​into all numbers within the selected fingerprint size Sz.
  
• After running a sufficient number of generated values, we have a two-dimensional histogram of the residual from division by all numbers in the selected range. Note that this histogram does not depend on the order in which values ​​are given by the generator. On the other hand, we could feed the histogram not the values ​​themselves, but their differences from the previous ones, for example, then the order would be partially taken into account.
  
• Next, we display the resulting histogram in an easy-to-see form ( gnuplot is used here in the ' pm3d map ' mode) and admire the picture that opens. It should be noted that the value does not fall into the output from Hists [ix] [[iy], but corrected taking into account the probability of hitting (Hists [ix] [iy] * (ix + 1) / Sz)
  

')
So, let's begin. And we begin with the standard C-shnogo rand generator:


As expected, the histogram turned out to be triangular and flat, but ... but what are these strange strips?
Consider more.



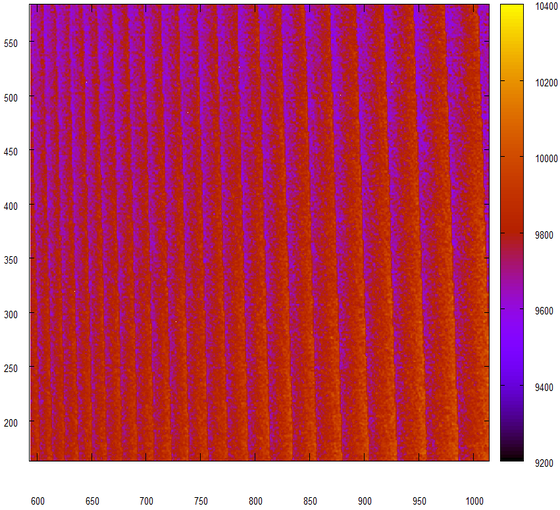
It seems that this generator produces not very random numbers. Well, I always suspected that using rand () as a random number generator is “a sure sign of a bad person” (C).

Perhaps you should look at the “correct” random number generator. As such, we will use this, kindly provided by Yuri Tkachev.



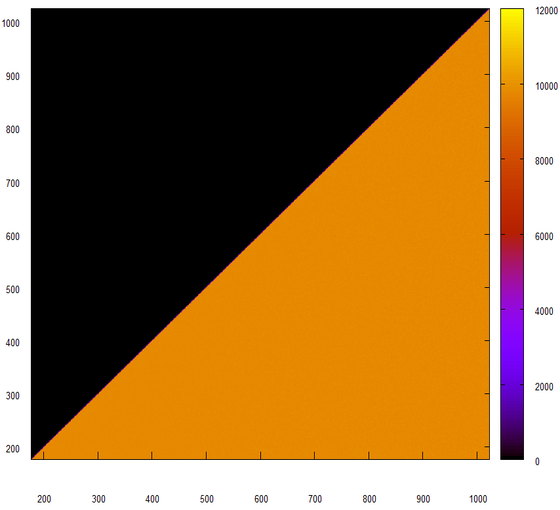
At first glance, it looks good. Let's look at this histogram.



Yes, this is exactly what we expected to get from a random number generator. Let's try to move the data a bit, we will take into account only the low 24 bits.



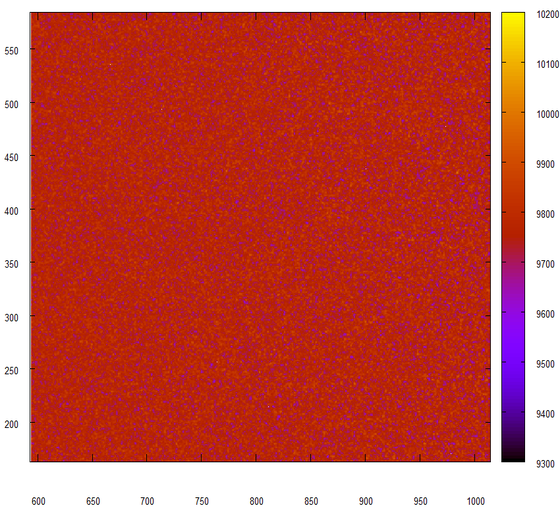
Nothing has changed, but that’s what we wanted to see. Another experiment, this time we will glue the pieces of 24 bits of two consecutive numbers, issued by our wonderful generator.



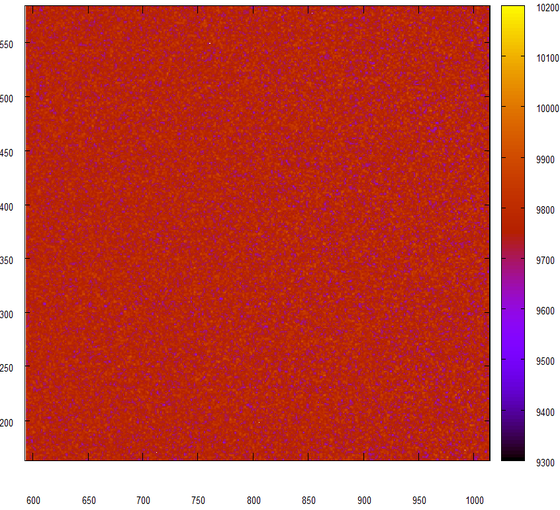
And again, no difference! Just wonderful!
The last attempt, this time we will not glue the 24-bit pieces, and multiply them.



Wham! And the feeling is that our pseudo-gut got out of our random number generator.
The same, but on a different scale:



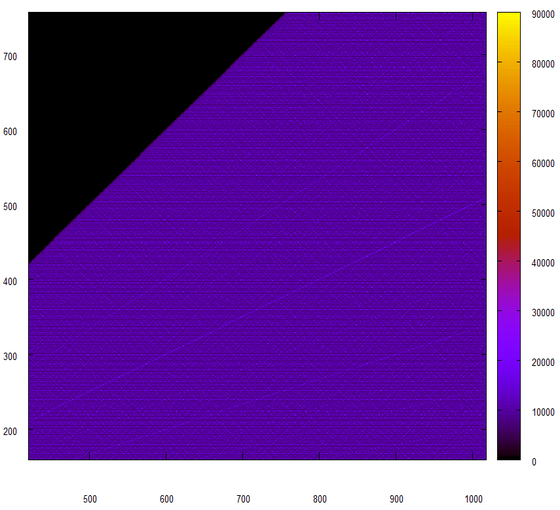
Oh, oh, "we said with Peter Ivanovich" (C).
To take a breath and gain time to understand what happened, let's see what other kind of data looks like:



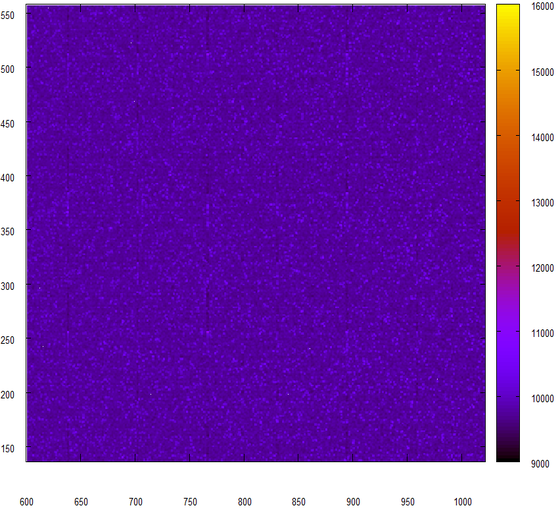
These are the first 10 million 64-bit integers subtracted from the file - the database image.



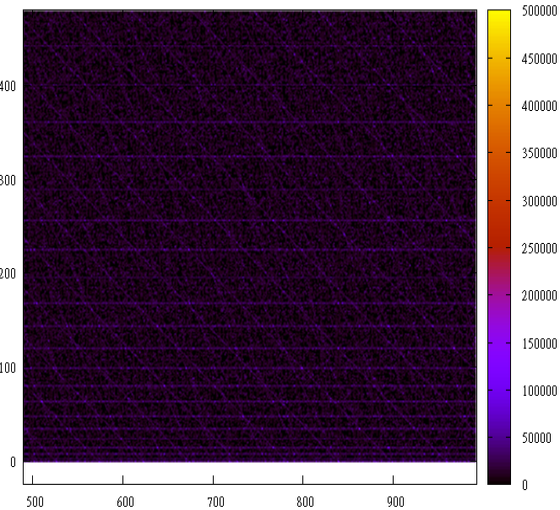
And this is the data obtained in the same way, the source of which served as a zip file.
It would look like random data, but vertical bars spoil everything.

So, while the attentive reader was amused by reading the data from the files, the author decided to see how very random sequences behave. We start with F (n) = F (n-1) + 1, i.e. 0, 1, 2, 3 ...

We will not look at the histogram of the sequence itself, it is triangular and completely flat, which is intuitive and easy to explain. In fact, since there is no order in our method, such a sequence behaves like an ideal random number generator, which covers the entire range with equal probability.
But the distribution of the product of two numbers, each from 0 to 4000 looks like this:



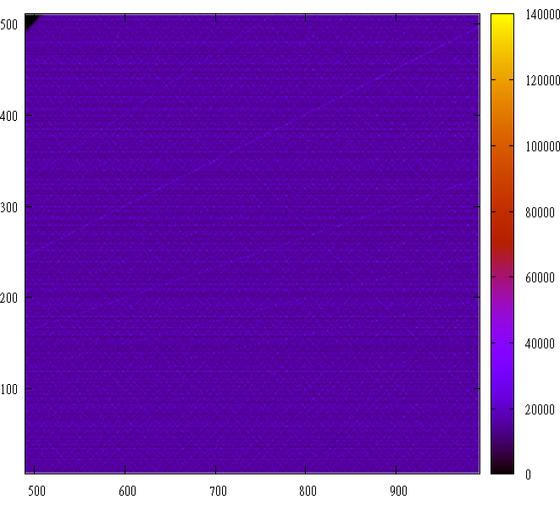
Very familiar picture, is not it. In fact, we see a reference sample of the histogram of the product of two numbers.
In one place came the product and the remnants of division .
In a rather simple way, we pulled the magic of numbers from under the floor.



And this is how the sequence F (n) = n * n behaves 0, 1, 4, 9 ...



And here F (n) = 2 * n * (2 * n + 1), i.e. 0 * 1, 2 * 3, 4 * 5 ...
And finally, the author could not refrain from showing the distribution of the first 10 million prime numbers.


And their “cast” - the first 10 million uneasy numbers (just beautiful).



Well, be careful and “always, no, never” (C) do not multiply the sequences :).

Ps. The author is grateful to Alexander Artyushin for an active discussion of subj.