Alternative tic-tac-toe
Once at a picnic, I noticed mathematicians crowding around the game, of which I had the least interest in anything: tic-tac-toe.
You might have noticed for yourself that the tic-tac-toe game is deadly boring. It has no place for a creative idea or a sudden insight. Good players always tied. The game inevitably goes something like this:

')
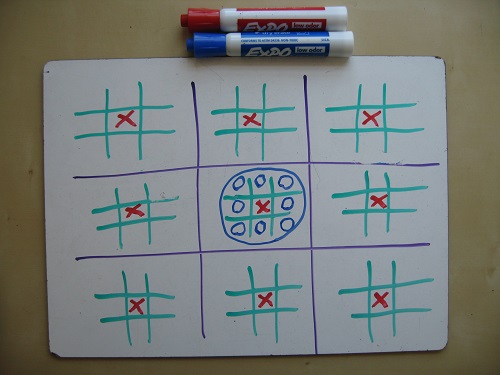
But the picnic mathematicians played a more sophisticated version of the game. In each of the cells in a square field, they drew a smaller field:

As I watched, I noticed the basic rules:
1. Each turn is made in one of the small fields.

2. Achieved in a small field the location of three identical figures in a row wins this field.
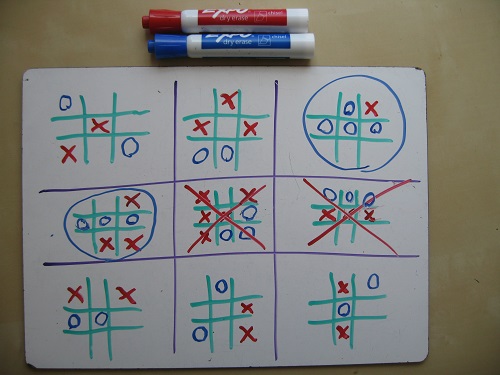
3. To win the game, you must win in three small fields in a row.

But to understand the most important rule, it took me some time:
The player does not choose one of the nine small fields in which he wants to walk. The choice is determined by your opponent's previous move. A cell in a small field that he went to is the small field in which you have to make a move. (And the cell into which you go, in turn, determines which small field your opponent will go to.) For example, if I go here ...

You will make your next move here ...

This gives the game an element of strategy. You cannot afford to focus on a small field. You have to consider where your turn will send your opponent, and where his next move will send you and so on.
The result looks very unusual. Players can move randomly, easily skipping designs in two and three identical pieces in a row. But there is order in this madness - they think through their moves ahead, remembering the possibility of sending an opponent to an unspoilt property. This is, in general, much more interesting than the usual tic-tac-toe.
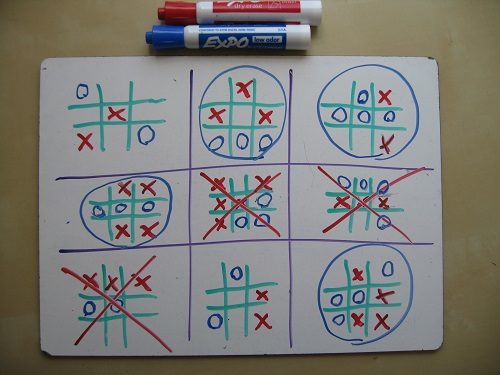
A couple of conventions are needed:
1. What if my opponent sends me to a small field in which a victory has already been won? This is a bad situation. If there are empty cells left there, you will have to choose one of them. Although you will not be able to influence the outcome of the game in this field, at least you will determine where your opponent will go.

2. What if my opponent sends me to a filled field? In this case, congratulations - you can choose any of the fields for your turn. (This means that you should avoid sending your opponent into the filled field!)
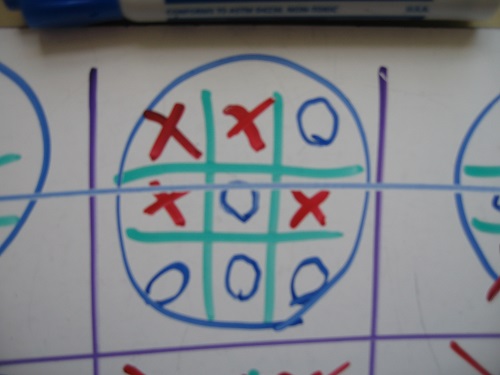
When I see my students playing tic-tac-toe, I hold back the urge to roll my eyes and show them this game. You can bet that the game develops mathematical skills (deductive reasoning, conditional thinking, the geometric idea of similarity), but what difference does it make? In any case, the game is good.
One last thing: I developed a strategy that I modestly named Gambit Orlin. You start by capturing the central cell itself.

Your opponent will have to put a zero in any of the other cells.

Go to the center again.

The toe starts to form a row.

Go to the center again.

Your opponent makes a winning row, laughing at your stupidity.

Go to the center again.

The opponent sees the trick you went to ...

Go to the center again. Your opponent reluctantly understands that it's impossible to stop you.
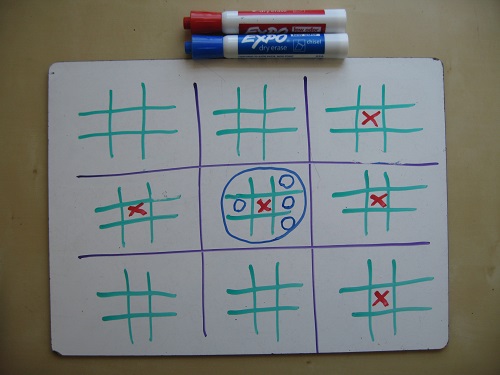
When finished, the crosses at the cost of a sacrifice central field have the best position in the other eight. This is in no way an ideal strategy. It stimulates the loss of the central field without a fight. But the forced useless accumulation of so many zeros in one field allows the crosses to get the upper hand throughout the rest of the game.
In short, this is an alternative tic-tac-toe. Play Let me know how you are doing.
Supplement June 18: A frequent (and intelligent) question: “What should I do if there is a draw in one of the small fields?” It looks like there are two options:
1. The field is considered neither for a cross, nor for a zero. (So I play.)
2. A field is counted for both a cross and a zero. (This will help avoid draws, although it can lead to a strange draw when you and your opponent win at the same time.)
I guess each of the options works. Just make sure that you and your opponent come to an agreement before starting the game, as this affects the strategy.
Translator's note: there is already an implementation of this game for the Android platform .
You might have noticed for yourself that the tic-tac-toe game is deadly boring. It has no place for a creative idea or a sudden insight. Good players always tied. The game inevitably goes something like this:

')
But the picnic mathematicians played a more sophisticated version of the game. In each of the cells in a square field, they drew a smaller field:

As I watched, I noticed the basic rules:
1. Each turn is made in one of the small fields.

2. Achieved in a small field the location of three identical figures in a row wins this field.

3. To win the game, you must win in three small fields in a row.

But to understand the most important rule, it took me some time:
The player does not choose one of the nine small fields in which he wants to walk. The choice is determined by your opponent's previous move. A cell in a small field that he went to is the small field in which you have to make a move. (And the cell into which you go, in turn, determines which small field your opponent will go to.) For example, if I go here ...

You will make your next move here ...

This gives the game an element of strategy. You cannot afford to focus on a small field. You have to consider where your turn will send your opponent, and where his next move will send you and so on.
The result looks very unusual. Players can move randomly, easily skipping designs in two and three identical pieces in a row. But there is order in this madness - they think through their moves ahead, remembering the possibility of sending an opponent to an unspoilt property. This is, in general, much more interesting than the usual tic-tac-toe.

A couple of conventions are needed:
1. What if my opponent sends me to a small field in which a victory has already been won? This is a bad situation. If there are empty cells left there, you will have to choose one of them. Although you will not be able to influence the outcome of the game in this field, at least you will determine where your opponent will go.

2. What if my opponent sends me to a filled field? In this case, congratulations - you can choose any of the fields for your turn. (This means that you should avoid sending your opponent into the filled field!)

When I see my students playing tic-tac-toe, I hold back the urge to roll my eyes and show them this game. You can bet that the game develops mathematical skills (deductive reasoning, conditional thinking, the geometric idea of similarity), but what difference does it make? In any case, the game is good.
One last thing: I developed a strategy that I modestly named Gambit Orlin. You start by capturing the central cell itself.

Your opponent will have to put a zero in any of the other cells.

Go to the center again.

The toe starts to form a row.

Go to the center again.

Your opponent makes a winning row, laughing at your stupidity.

Go to the center again.

The opponent sees the trick you went to ...

Go to the center again. Your opponent reluctantly understands that it's impossible to stop you.

When finished, the crosses at the cost of a sacrifice central field have the best position in the other eight. This is in no way an ideal strategy. It stimulates the loss of the central field without a fight. But the forced useless accumulation of so many zeros in one field allows the crosses to get the upper hand throughout the rest of the game.

In short, this is an alternative tic-tac-toe. Play Let me know how you are doing.
Supplement June 18: A frequent (and intelligent) question: “What should I do if there is a draw in one of the small fields?” It looks like there are two options:
1. The field is considered neither for a cross, nor for a zero. (So I play.)
2. A field is counted for both a cross and a zero. (This will help avoid draws, although it can lead to a strange draw when you and your opponent win at the same time.)
I guess each of the options works. Just make sure that you and your opponent come to an agreement before starting the game, as this affects the strategy.
Translator's note: there is already an implementation of this game for the Android platform .
Source: https://habr.com/ru/post/183764/
All Articles