Algorithm seam carving for image resizing
Seam carving is an algorithm for resizing an image that preserves important content and removes less significant content. It was described in an article by S. Avidan & A. Shamir . It gives a better result than the usual stretching of the image in view of the fact that it does not change the proportions of the significant elements of the image. The two photos below demonstrate the operation of the algorithm - the original image has a size of 332x480, while the modified seam carving is 272x400.


In this article I will describe the operation of the algorithm using pseudocode and Matlab code. The original article written by me in English is available here , the source code on githabe .
In order to simplify the presentation, I will describe only the case of reducing the size of the image. Enlarging a picture is a similar process.
The idea of the algorithm is to remove content that has less value for the user (contains less information). We will call the measure of this information "energy." As such a function, we can use an image gradient in the space l1: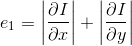
If the picture has 3 channels, then as the gradient of the entire image we use the sum of the gradients of each channel. The Matlab code below demonstrates this approach:
And this is the result of applying the energy function to the image used:

If we remove the pixels with the minimum energy, but an arbitrary position, then the image will be damaged. If we remove the columns / columns with minimal energy, unwanted artifacts will appear. Here, under the column, I mean {(i, j) | j is fixed}, and under the column {(i, j) | i fixed}. The solution to the dilemma is to introduce a generalization of the notion of a column / column.
Formally, let I be the nxm image, then we call it vertical seam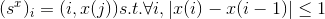 ,
,
where x: [1, .., n] -> [1, .., m]. That is, the vertical seam is a path from the top of the image to the bottom such that the length is the width of the image, and for each element (i, j) belonging to the seam, the next element can only be (i + 1, j-1), (i +1, j), (i + 1, j +1). Similarly, we can enter a horizontal seam. Examples of vertical and horizontal seams are shown below:

We are interested in seams with minimal energy.
To find such a seam, we use dynamic programming:
For efficiency, in the Matlab code, I represent seam using the nxm bit matrix. If the pixel belongs to seam, it is marked 0, otherwise 1.
To find the horizontal seam, simply pass the transposed energy matrix to the findOptSeam function.
')
So, now we can find the minimum seam and using the code below we can remove it from the image:
This set of operations is already enough to change the image size in width or height, keeping important details - just remove as much as you need horizontal and vertical seams.
But what if we need to simultaneously reduce the size of the image vertically and horizontally? How to understand at each iteration what is better in terms of energy minimization - to remove the vertical seam or horizontal?
This problem can again be solved by dynamic programming. Let n 'and m' be the desired image size (n '<n, m' <m). We introduce the matrix T, which determines for each n 'x m' the cost of the optimal sequence of removal of the vertical and horizontal seams. For convenience, we introduce r = n - n ', m = m - m', which describe the number of vertical and horizontal deletions. In addition to T, we introduce the TBM matrix of size rxc, which for each T (i, j) stores 0 or 1, depending on whether we came to T (i, j) by removing the vertical (1) or horizontal (0) seam. The pseudocode is shown below:
And the implementation on Matlab:
The algorithm works well on landscape images, see the gif demonstrating the dynamics of the algorithm (thanks to shara ):

But as is, it is poorly suited for portraits or images full of detail. On landscape images, the sky or the sea contains little information, and the image is usually reduced by them. If you take an image containing many small details, the algorithm will not give the best result (an example is taken from the article Avidan & A. Shamir):

Without user input, seam carving should not be applied to portrait photographs, since a meaningful object for us - a person - contains less information in terms of seam carving:

The algorithm can be applied to remove tagged objects from an image (an example is taken from the Avidan & A. Shamir article):



In this article I will describe the operation of the algorithm using pseudocode and Matlab code. The original article written by me in English is available here , the source code on githabe .
Energy image
In order to simplify the presentation, I will describe only the case of reducing the size of the image. Enlarging a picture is a similar process.
The idea of the algorithm is to remove content that has less value for the user (contains less information). We will call the measure of this information "energy." As such a function, we can use an image gradient in the space l1:
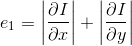
If the picture has 3 channels, then as the gradient of the entire image we use the sum of the gradients of each channel. The Matlab code below demonstrates this approach:
function res = energyRGB(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = energyGrey(I(:, :, 1)) + energyGrey(I(:, :, 2)) + energyGrey(I(:, :, 3)); end function res = energyGrey(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = abs(imfilter(I, [-1,0,1], 'replicate')) + abs(imfilter(I, [-1;0;1], 'replicate')); end And this is the result of applying the energy function to the image used:

Seam
If we remove the pixels with the minimum energy, but an arbitrary position, then the image will be damaged. If we remove the columns / columns with minimal energy, unwanted artifacts will appear. Here, under the column, I mean {(i, j) | j is fixed}, and under the column {(i, j) | i fixed}. The solution to the dilemma is to introduce a generalization of the notion of a column / column.
Formally, let I be the nxm image, then we call it vertical seam
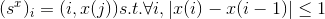 ,
,where x: [1, .., n] -> [1, .., m]. That is, the vertical seam is a path from the top of the image to the bottom such that the length is the width of the image, and for each element (i, j) belonging to the seam, the next element can only be (i + 1, j-1), (i +1, j), (i + 1, j +1). Similarly, we can enter a horizontal seam. Examples of vertical and horizontal seams are shown below:

We are interested in seams with minimal energy.
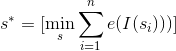
To find such a seam, we use dynamic programming:
- Finding the matrix M of the minimum energy for all possible seams for each (i, j):
- Fill the first line M with values from the energy matrix e
- For all lines, starting with the second:
M [i, j] = e [i, j] + min (M [i - 1, j], M [i, j], M [i +1, j]);
- Find the minimum value in the last row of the matrix M and build a path from this pixel to the first row, choosing at each step a piekel with minimum energy (similarly, for (i, j) consider the values of M in the positions [i - 1, j], [i , j], [i + 1, j]).
For efficiency, in the Matlab code, I represent seam using the nxm bit matrix. If the pixel belongs to seam, it is marked 0, otherwise 1.
function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end To find the horizontal seam, simply pass the transposed energy matrix to the findOptSeam function.
')
Finding the optimal order of removal seams
So, now we can find the minimum seam and using the code below we can remove it from the image:
function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end This set of operations is already enough to change the image size in width or height, keeping important details - just remove as much as you need horizontal and vertical seams.
But what if we need to simultaneously reduce the size of the image vertically and horizontally? How to understand at each iteration what is better in terms of energy minimization - to remove the vertical seam or horizontal?
This problem can again be solved by dynamic programming. Let n 'and m' be the desired image size (n '<n, m' <m). We introduce the matrix T, which determines for each n 'x m' the cost of the optimal sequence of removal of the vertical and horizontal seams. For convenience, we introduce r = n - n ', m = m - m', which describe the number of vertical and horizontal deletions. In addition to T, we introduce the TBM matrix of size rxc, which for each T (i, j) stores 0 or 1, depending on whether we came to T (i, j) by removing the vertical (1) or horizontal (0) seam. The pseudocode is shown below:
- T (0, 0) = 0;
- Initialize the values of T on the border:
for all j {
T (0, j) = T (0, j - 1) + E (seamVertical);
}
for all i {
T (i, 0) = T (j - 1, 0) + E (seamHorizontal);
} - Initialize the TBM values on the border:
for all j {T (0, j) = 1; }
for all i {T (0, i) = 0; } - Fill T and TBM:
for i = 2 to r {
imageWithoutRow = image;
for j = 2 to c {
energy = computeEnergy (imageWithoutRow);
horizontalSeamEnergy = findHorizontalSeamEnergy (energy);
verticalSeamEnergy = findVerticalSeamEnergy (energy);
tVertical = T (i - 1, j) + verticalSeamEnergy;
tHorizontal = T (i, j - 1) _ horizontalSeamEnergy;
if (tVertical <tHorizontal) {
T (i, j) = tVertical;
transBitMask (i, j) = 1
} else {
T (i, j) = tHorizontal;
transBitMask (i, j) = 0
}
// move from left to right - delete vertical seam
imageWithoutRow = removeVerticalSeam (energy);
}
energy = computeEnergy (image);
image = removeHorizontalSeam (energy);
} - Finding a path from T (r, c) to T (1, 1), deleting a row or column depending on the TBM value (i, j).
And the implementation on Matlab:
function [T, transBitMask] = findTransportMatrix(sizeReduction, image) % find optimal order of removing raws and columns T = zeros(sizeReduction(1) + 1, sizeReduction(2) + 1, 'double'); transBitMask = ones(size(T)) * -1; % fill in borders imageNoRow = image; for i = 2 : size(T, 1) energy = energyRGB(imageNoRow); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageNoRow, optSeamMask, 0); transBitMask(i, 1) = 0; T(i, 1) = T(i - 1, 1) + seamEnergyRow; end; imageNoColumn = image; for j = 2 : size(T, 2) energy = energyRGB(imageNoColumn); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageNoColumn, optSeamMask, 1); transBitMask(1, j) = 1; T(1, j) = T(1, j - 1) + seamEnergyColumn; end; % on the borders, just remove one column and one row before proceeding energy = energyRGB(image); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); image = reduceImageByMask(image, optSeamMask, 0); energy = energyRGB(image); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); image = reduceImageByMask(image, optSeamMask, 1); % fill in internal part for i = 2 : size(T, 1) imageWithoutRow = image; % copy for deleting columns for j = 2 : size(T, 2) energy = energyRGB(imageWithoutRow); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageWithoutRow, optSeamMaskRow, 0); [optSeamMaskColumn, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageWithoutRow, optSeamMaskColumn, 1); neighbors = [(T(i - 1, j) + seamEnergyRow) (T(i, j - 1) + seamEnergyColumn)]; [val, ind] = min(neighbors); T(i, j) = val; transBitMask(i, j) = ind - 1; % move from left to right imageWithoutRow = imageNoColumn; end; energy = energyRGB(image); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); % move from top to bottom image = reduceImageByMask(image, optSeamMaskRow, 0); end; end Conclusion
The algorithm works well on landscape images, see the gif demonstrating the dynamics of the algorithm (thanks to shara ):

But as is, it is poorly suited for portraits or images full of detail. On landscape images, the sky or the sea contains little information, and the image is usually reduced by them. If you take an image containing many small details, the algorithm will not give the best result (an example is taken from the article Avidan & A. Shamir):

Without user input, seam carving should not be applied to portrait photographs, since a meaningful object for us - a person - contains less information in terms of seam carving:

The algorithm can be applied to remove tagged objects from an image (an example is taken from the Avidan & A. Shamir article):

Source: https://habr.com/ru/post/183638/
All Articles