Functors, applicative functors and monads in pictures
Here is some simple meaning:

And we know how to apply the function to it:
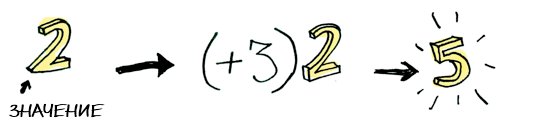
Elementary. So now let's complicate the task - let our meaning have a context. For now, you can think of context simply as a box where you can put a value:
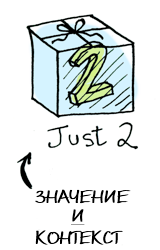
')
Now, when you apply a function to this value, you will get different results - depending on the context . This is the basic idea on which functors, applicative functors, monads, arrows, etc. are based. The
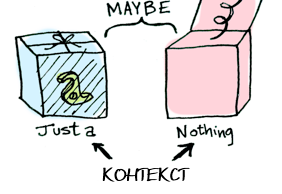
Later we will see the difference in the behavior of the function for
When you have a value wrapped in a context, you cannot simply take and apply the usual function to it:

And here
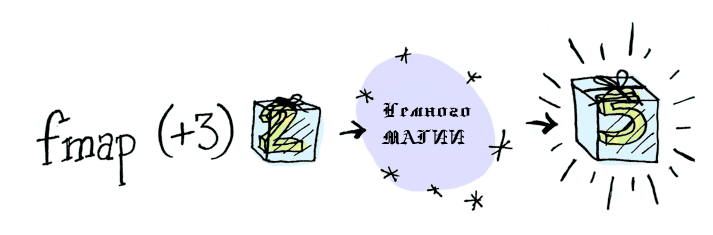
Bam!
A functor is a class of types . Here is its definition:
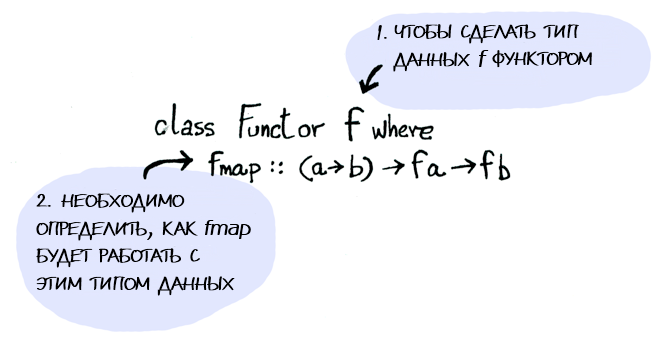
A functor is any data type for which it is defined how

So we can do this:
And
This is what happens behind the scenes when we write

And then you say: "Ok,


Bill O'Reilly does not understand anything in the Maybe functor.
Like Morpheus in The Matrix,
On Haskell:
If
Here is another example: what happens when you apply a function to a list?
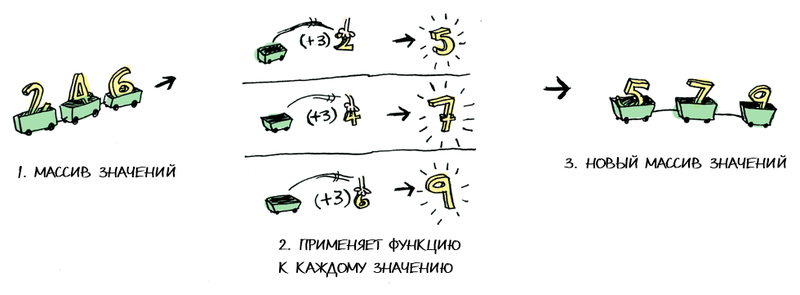
Lists are functors too! Here is the definition:
Okay, okay, another (last) example: what happens when you apply a function to another function?
Here is the function:

But the function applied to another function:
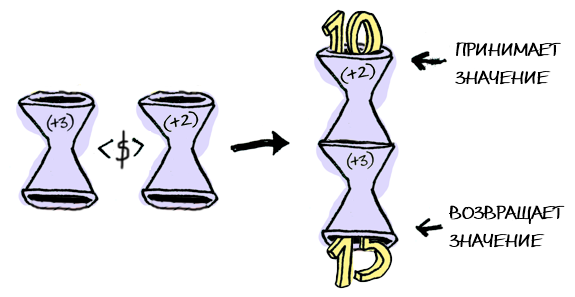
The result is just another function!
So functions are functors too!
And when you apply
The next level is applicative functors. With them, our value is still packed in context (as well as with functors):

But now our function is packed in context!

Aha Let's get into this. Applicative functors are not engaged in cheating.

Those.
Using
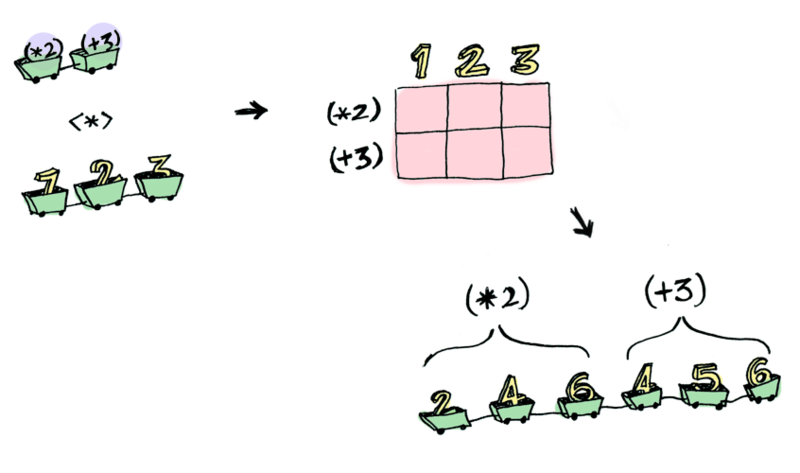
And here is something that you can do with applicative functors, but you cannot do it with ordinary ones. How do you apply a function that takes two arguments to two packed values?
Applicative functors:

The applicative functor observes how the ordinary uses the function.
And yes! There is a
How to learn monads:
Monads add a new twist to our story.
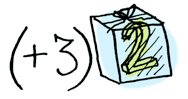
Functors apply a regular function to a packed value:
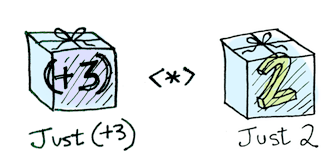
Applicative functors apply a packed function to the same packed value:
Monads apply a function that returns a packed value to a packed value. Monads have a function
Consider this example: our good old

Just a loose monad
Let

And what if we feed her the packed value?

We need to use

And here is how it works:
What happens inside?
Where
So
But what actions are done over the poor

If you give
You can also link a chain of calls:


Cool stuff! And now we know that
And now let's switch to another example:

In particular, on its three functions.



All three functions take regular values (or no values at all) and return packed values. So we can chain them with
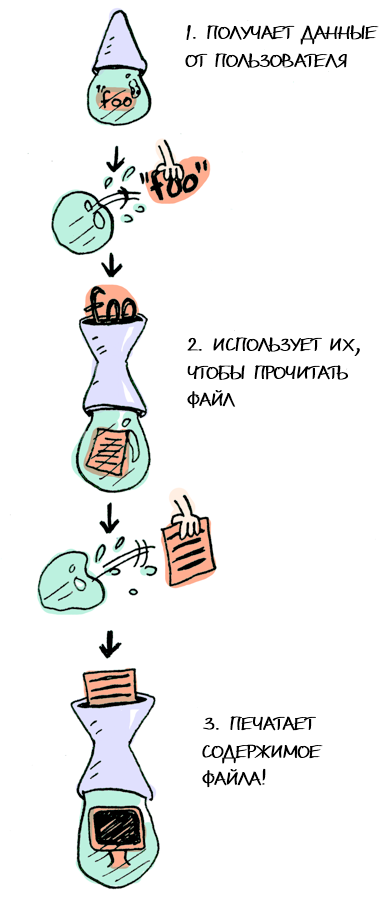
Oh yes, we have tickets in the first row for the "Monad-show"!
Haskell also provides us with some syntactic sugar for monads, called
What is the difference between these three?

So, dear friends (and I hope that by this time we have become friends), I think we all agree that monads are simple and a CLEAR IDEA (tm). And now, after we wet our throats with this manual, then why not call Mel Gibson and not finish the bottle to the bottom? Check out the monad section at LYAH. There are a lot of things that I didn’t say, because Miran did a great job of digging into this material.
More monads and pictures can be found in three useful monads ( translation ).
From the translator:
Link to the original: http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html I write it this way because Habr swears on url with commas.
And, of course, I would be very grateful for the comments in PM regarding the translation.

And we know how to apply the function to it:
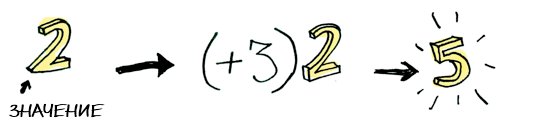
Elementary. So now let's complicate the task - let our meaning have a context. For now, you can think of context simply as a box where you can put a value:

')
Now, when you apply a function to this value, you will get different results - depending on the context . This is the basic idea on which functors, applicative functors, monads, arrows, etc. are based. The
Maybe data type defines two related contexts:
data Maybe a = Nothing | Just a Later we will see the difference in the behavior of the function for
Just a versus Nothing . But first, let's talk about functors!Functors
When you have a value wrapped in a context, you cannot simply take and apply the usual function to it:

And here
fmap to the rescue. fmap is a guy from the street, fmap knows a lot about contexts. He knows how to apply a function to a value wrapped in a context. Let's say that you want to apply (+3) to Just 2 . Use fmap : > fmap (+3) (Just 2) Just 5 
Bam!
fmap showed us how to do it! But how does he know how to properly apply a function?So what is a functor really?
A functor is a class of types . Here is its definition:

A functor is any data type for which it is defined how
fmap is applied to it. This is how fmap works:
So we can do this:
> fmap (+3) (Just 2) Just 5 And
fmap magically apply this function, because Maybe is a functor. It defines how to apply functions to Just 's and Nothing 's: instance Functor Maybe where fmap func (Just val) = Just (func val) fmap func Nothing = Nothing This is what happens behind the scenes when we write
fmap (+3) (Just 2) :
And then you say: "Ok,
fmap , and apply, please, (+3) to Nothing ."
> fmap (+3) Nothing Nothing 
Bill O'Reilly does not understand anything in the Maybe functor.
Like Morpheus in The Matrix,
fmap knows what to do; you started with Nothing and finish with Nothing too! This is fmap zen. And now it is clear why the data type Maybe exists. For example, how would you work with a record in a database in a language without Maybe : post = Post.find_by_id(1) if post return post.title else return nil end On Haskell:
fmap (getPostTitle) (findPost 1) If
findPost returns a message, then we display its header using getPostTitle . If it returns Nothing , then we return Nothing ! Damn graceful, huh?<$> Is the infix version of fmap , so instead of the code above you can often find: getPostTitle <$> (findPost 1) Here is another example: what happens when you apply a function to a list?

Lists are functors too! Here is the definition:
instance Functor [] where fmap = map Okay, okay, another (last) example: what happens when you apply a function to another function?
fmap (+3) (+1) Here is the function:

But the function applied to another function:

The result is just another function!
> import Control.Applicative > let foo = fmap (+3) (+2) > foo 10 15 So functions are functors too!
instance Functor ((->) r) where fmap fg = f . g And when you apply
fmap to a function, you simply make a composition of functions!Applicative Functors
The next level is applicative functors. With them, our value is still packed in context (as well as with functors):

But now our function is packed in context!

Aha Let's get into this. Applicative functors are not engaged in cheating.
Control.Applicative defines a <*> that knows how to apply a function wrapped in a context to a value wrapped in a context :
Those.
Just (+3) <*> Just 2 == Just 5 Using
<*> can lead to interesting situations. For example: > [(*2), (+3)] <*> [1, 2, 3] [2, 4, 6, 4, 5, 6] 
And here is something that you can do with applicative functors, but you cannot do it with ordinary ones. How do you apply a function that takes two arguments to two packed values?
> (+) <$> (Just 5) Just (+5) > Just (+5) <$> (Just 4) ??? JUST Applicative functors:
> (+) <$> (Just 5) Just (+5) > Just (+5) <*> (Just 3) Just 8 Applicative technically pushes Functor aside. “The big guys can use functions with any number of arguments,” he says. “Armed with <$> and <*> , I can take any function that expects any number of unpacked arguments. Then I will give her all the packed values and get the same packed result! BVAHAHAHAHAHAHA! " > (*) <$> Just 5 <*> Just 3 Just 15 
The applicative functor observes how the ordinary uses the function.
And yes! There is a
liftA2 function that does the same thing: > liftA2 (*) (Just 5) (Just 3) Just 15 Monads
How to learn monads:
- Get PhD Crusts in Computer Science
- Throw them nafig, because when reading this section you will not need them!
Monads add a new twist to our story.
Functors apply a regular function to a packed value:

Applicative functors apply a packed function to the same packed value:

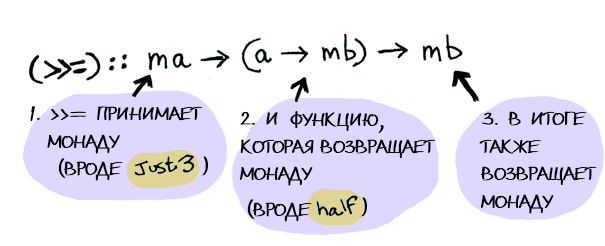
Monads apply a function that returns a packed value to a packed value. Monads have a function
>>= (pronounced “binding” ( bind )), which allows to do this.Consider this example: our good old
Maybe - this is a monad:
Just a loose monad
Let
half be a function that works only with even numbers: half x = if even x then Just (x `div` 2) else Nothing 
And what if we feed her the packed value?

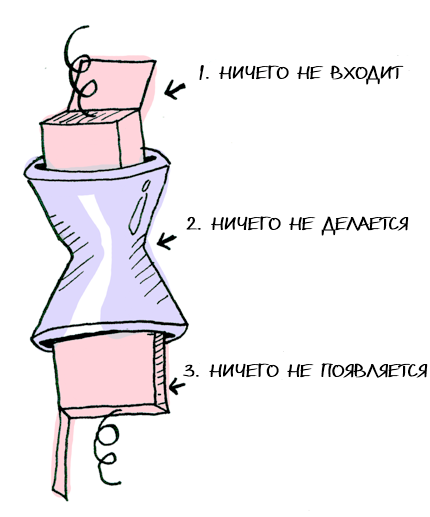
We need to use
>>= to push the packed value through the function. Here's a photo >>= :
And here is how it works:
> Just 3 >>= half Nothing > Just 4 >>= half Just 2 > Nothing >>= half Nothing What happens inside?
Monad is another type class. Here is its partial definition: class Monad m where (>>=) :: ma -> (a -> mb) -> mb Where
>>= :
So
Maybe is a monad: instance Monad Maybe where Nothing >>= func = Nothing Just val >>= func = func val But what actions are done over the poor
Just 3 !
If you give
Nothing to the input, it is still easier:
You can also link a chain of calls:
> Just 20 >>= half >>= half >>= half Nothing 

Cool stuff! And now we know that
Maybe is Functor , Applicative and Monad in one person.And now let's switch to another example:
IO monad:
In particular, on its three functions.
getLine takes no arguments and gets user data from login:
getLine :: IO String readFile takes a string (file name) and returns its contents:
readFile :: FilePath -> IO String putStrLn takes a string and prints it:
putStrLn :: String -> IO () All three functions take regular values (or no values at all) and return packed values. So we can chain them with
>>= !
getLine >>= readFile >>= putStrLn Oh yes, we have tickets in the first row for the "Monad-show"!
Haskell also provides us with some syntactic sugar for monads, called
do notation: foo = do filename <- getLine contents <- readFile filename putStrLn contents Conclusion
- A functor is a data type that is implemented using the
Functortype class. - An applicative functor is a data type that is implemented using the
Applicativetype class. - A monad is a data type that is implemented using the
Monadtype class. - Maybe is implemented using all three types of types, so it is a functor, an applicative functor, and a monad at the same time.
What is the difference between these three?

- functor : you apply a function to a packed value using
fmapor<$> - applicative functor : you apply a packed function to a packed value using
<*>orliftA - monad : you apply a function that returns a packed value to a packed value using
>>=orliftM
So, dear friends (and I hope that by this time we have become friends), I think we all agree that monads are simple and a CLEAR IDEA (tm). And now, after we wet our throats with this manual, then why not call Mel Gibson and not finish the bottle to the bottom? Check out the monad section at LYAH. There are a lot of things that I didn’t say, because Miran did a great job of digging into this material.
More monads and pictures can be found in three useful monads ( translation ).
From the translator:
Link to the original: http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html I write it this way because Habr swears on url with commas.
And, of course, I would be very grateful for the comments in PM regarding the translation.
Source: https://habr.com/ru/post/183150/
All Articles