A soft introduction to Coq: use tactics

Proof by simplification

So, in the previous parts we defined new data types and functions on them. It is time to address the question of how to formulate and prove their properties and behavior. In a sense, we have already begun to do this — in the first part, we wrote a kind of unit test using the Example keyword, which contained some statements about the behavior of a certain function applied to a specific set of arguments. Using the definition of a function, Coq simplifies the expression and checks its left and right parts for equality.

This kind of evidence can be used for a fairly wide range of tasks. Let us show that 0 is a neutral element for the left addition operation:

 Theorem plus_O_n: forall n: nat, 0 + n = n.
 Proof.
   simpl.  reflexivity.  Qed.

The reflexivity command implicitly simplifies both sides of an expression before comparing.
')
The keywords simpl and reflexivity are examples of tactics. The main goal of tactics is to tell Coq how to check the correctness of the necessary statements. There is a rather narrow circle of problems whose correctness can be automatically proved. Prove that 2 + 2 = 4:

 Coq <Lemma using_auto: 2 + 2 = 4.
 1 subgoal
  
   ============================
    2 + 2 = 4

 using_auto <Proof.  auto.  Qed.

 Proof completed.

 auto.

 using_auto is defined

In most cases, it is necessary to use tactics.

intros tactics

In addition to unit tests that apply functions to a set of arguments, we will be interested in proving the properties of programs whose formulation contains mathematical quantifiers (for example, “for all natural numbers n ”) and hypotheses (for example, “let a = b ”). The intros tactic allows intros to transfer quantifiers and hypotheses from statements to the context of current arguments. Let us prove that the result of multiplying the left of any natural number by zero is zero:

 Theorem mult_zero: forall n: nat, 0 * n = 0.
 Proof.  intros n.  reflexivity.  Qed.

Proof overwrite

Consider a more interesting example:

 Theorem plus_id_example: forall nm: nat,
 n = m ->
 n + m = m + n.

Instead of formulating and proving a universal statement for any n and m , this theorem speaks of narrower properties that take place for n = m . Since n and m are arbitrary numbers, we cannot use simplification for the proof. Instead, we will prove that replacing m with n in the condition (assuming n = m ), we obtain the correct identity. The tactic that tells Coq to make this change is called rewrite :

 Proof.
  intros n m.
  intros H.
  rewrite -> H.
  reflexivity.  Qed.

In order to better understand what happened here, I strongly recommend that you run this example in CoqIDE and go through this evidence step by step.

So, we formulate the theorem and begin the proof:



The next step is to transfer the expressions from under the quantifiers of universality and hypothesis into the current context of the proof (in the upper right part of CoqIDE, we observe how the current context of the proof changes):



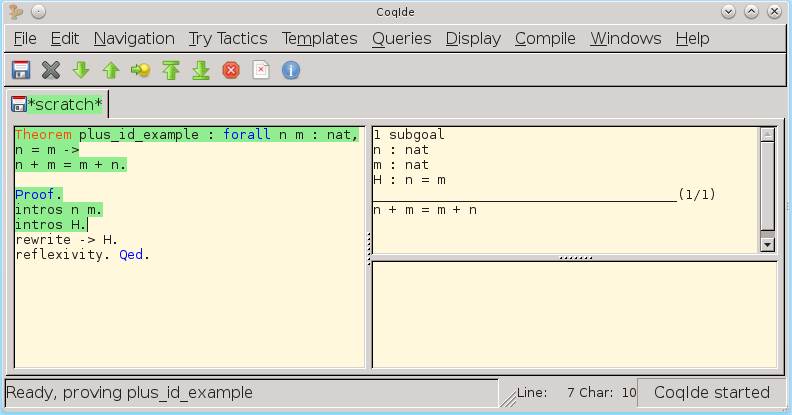
We rewrite the current goal of the proof:



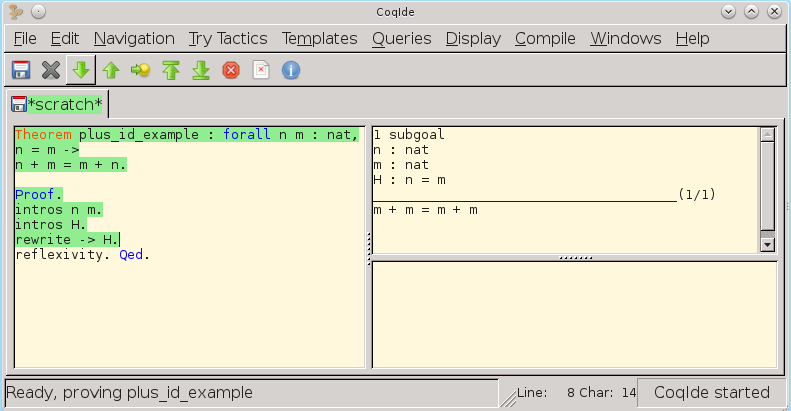
We finish the proof with simplification:

Conclusion

In the next part, we will introduce more advanced tactics and start working with data structures in Coq. Once again I draw the reader's attention to the importance of self-launching examples in CoqIDE.

Links to previous parts:

1. Start
2. Inductive definitions .