Gentle introduction to Coq: inductive definitions
In the previous section, we learned how to define new types and build functions over their values. In this short note I will focus on inductive definitions in more detail in order to clarify and outline further topics for study.
Earlier, I said that there are no batteries in Coq. In fact, I was a goof - Coq has a standard library that contains many useful definitions. In addition to the standard library, there are more specific things that we will not dwell on yet.
When CoqIDE starts up in the background, some libraries are being browsed, a list of which can be viewed using the
For academic purposes, we will not use the definitions from these libraries.
')
As you know, no introductory article on functional programming is complete without factorial calculation. We will not depart from this tradition and write our own factorial with inductive types.
Inductive definitions are found everywhere in mathematics. For example, natural numbers from the standpoint of set theory are introduced as follows:
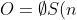&space;=&space;n&space;\cup&space;\left&space;\{&space;n&space;\right&space;\})
Similarly, we can specify natural numbers in Coq. In order not to litter the namespace, we will use the system of modules:
This ad should read like this:
Using this definition, we can construct any natural number:
Now that we have natural numbers, it's time to define a set of functions over these numbers:
Here we have defined the recursive (keyword
Consider her work on a specific example. Calculate the value of the expression 3 + 2:
Fine! Everything is working. But how is this result?
Similarly, you can write the multiplication function and implement factorial computation, without which no functional programming tutorial can do:
To consolidate the material, I highly recommend the reader to run all the examples in CoqIDE. In the next part we will look at how to work with basic Coq tactics.
Continued .
Earlier, I said that there are no batteries in Coq. In fact, I was a goof - Coq has a standard library that contains many useful definitions. In addition to the standard library, there are more specific things that we will not dwell on yet.
When CoqIDE starts up in the background, some libraries are being browsed, a list of which can be viewed using the
Print Libraries command:Loaded and imported library files: Coq.Init.Notations Coq.Init.Logic Coq.Init.Datatypes Coq.Init.Specif Coq.Init.Peano Coq.Init.Wf Coq.Init.Tactics Coq.Init.Prelude Coq.Init.Logic_Type
For academic purposes, we will not use the definitions from these libraries.
')
As you know, no introductory article on functional programming is complete without factorial calculation. We will not depart from this tradition and write our own factorial with inductive types.
Integers
Inductive definitions are found everywhere in mathematics. For example, natural numbers from the standpoint of set theory are introduced as follows:
Similarly, we can specify natural numbers in Coq. In order not to litter the namespace, we will use the system of modules:
Module Test1. Inductive nat: Type: = | O: nat | S: nat -> nat.
This ad should read like this:
- O is a natural number
- S is a constructor that takes a positive integer and returns another positive integer: if n ∈ N, then S n ∈ N.
Using this definition, we can construct any natural number:
Eval simpl in (SO). (* ==> 1: nat *) Eval simpl in (S (SO)). (* ==> 2: nat *) Eval simpl in (S (S (SO))). (* ==> 3: nat *)
Now that we have natural numbers, it's time to define a set of functions over these numbers:
Fixpoint plus (n: nat) (m: nat): nat: =
match n with
| O => m
| S n '=> S (plus n' m)
end.
Here we have defined the recursive (keyword
Fixpoint ) function plus , which takes two arguments of type nat as input and returns the result of type nat . You can verify this with the Check command:Check plus. (* ==> plus: nat -> nat -> nat *)
Consider her work on a specific example. Calculate the value of the expression 3 + 2:
Eval simpl in (plus (S (S (SO))) (S (SO))). (* ==> 5: nat *)
Fine! Everything is working. But how is this result?
(* plus (S (S (SO))) (S (SO)) ==> S (plus (S (SO)) (S (SO))) second clause in the definition ==> S (S (plus (SO) (S (SO)))) second clause in the definition ==> S (S (S (plus O (S (SO))))) second clause in the definition ==> S (S (S (S (SO)))) the first clause in the definition *)
Similarly, you can write the multiplication function and implement factorial computation, without which no functional programming tutorial can do:
Fixpoint mult (nm: nat): nat: =
match n with
| O => o
| S n '=> plus m (mult n' m)
end.
Fixpoint factorial (n: nat): nat: =
match n with
| O => SO
| S n '=> mult n (factorial n')
end.
Eval simpl in (factorial (S (S (S (S (SO)))))).
(* ==> 120: nat *)
Conclusion
To consolidate the material, I highly recommend the reader to run all the examples in CoqIDE. In the next part we will look at how to work with basic Coq tactics.
Continued .
Source: https://habr.com/ru/post/182748/
All Articles