About proteins and complex networks
In pursuit of a post about squirrels, I will try to talk about a topic that seems to be unrelated to biology as complex networks.
A complex network is graphs with nontrivial topological properties. By nontrivial topological properties, we usually mean that the links between nodes of a graph are distributed according to a clever law, which in turn gives rise to various cluster structures, hubs, vulnerabilities, and so on.
The concept of a complex network grew out of the idea of tracking down citations of scientific papers in the 50s of the last century, and slowly grew, capturing the Internet, social networks, road networks and even many areas of theoretical physics, right up to quantum. The pioneer of complex networks was the Hungarian mathematician Paul Erdős, who published dozens of articles on network theory and related problems. It is curious that in his honor in the scientific community, quoting in jest began to measure Erdoch’s numbers. This is a comic metric that shows the length of the connection between Erdos and another author on the co-author's network. That is, if Vasily Pupkin is a co-author of Alfred Renyi, who in turn is co-author of Erdosh, then Vasily has Erdoch's number two (Paul and Alfred have zero and one respectively).
One of the key problems (and, as a consequence, properties) in the theory of complex networks is the problem of splitting a network into clusters. A cluster is an array of nodes that are connected to each other more than the rest of the network. Now there are dozens, if not hundreds of clustering algorithms, but all have limitations and drawbacks: either they are too slow, or the computational time increases astronomically with the number of nodes, or the accuracy suffers depending on the conditions of the initial problem. In this article, the gradient cluster algorithm will be used, the essence of which is as follows: for each node, we leave only the maximum connection with the other node (thus excluding self-communication), removing all the others. Thus, the network will be divided into subnets, which will be clusters.
')
In the upper picture, clusters are easy to find and “by eye”, and on the bottom?


Why is all this necessary? The fact is that proteins under the influence of external factors (temperature, pressure, ions, water, etc.) can be in different states (conformations) that correspond to various biological functions that are not always useful. Usually states describe some parameter or several parameters (order parameter), such as radius of inertia, number of hydrogen bonds, distance between certain atoms, etc.
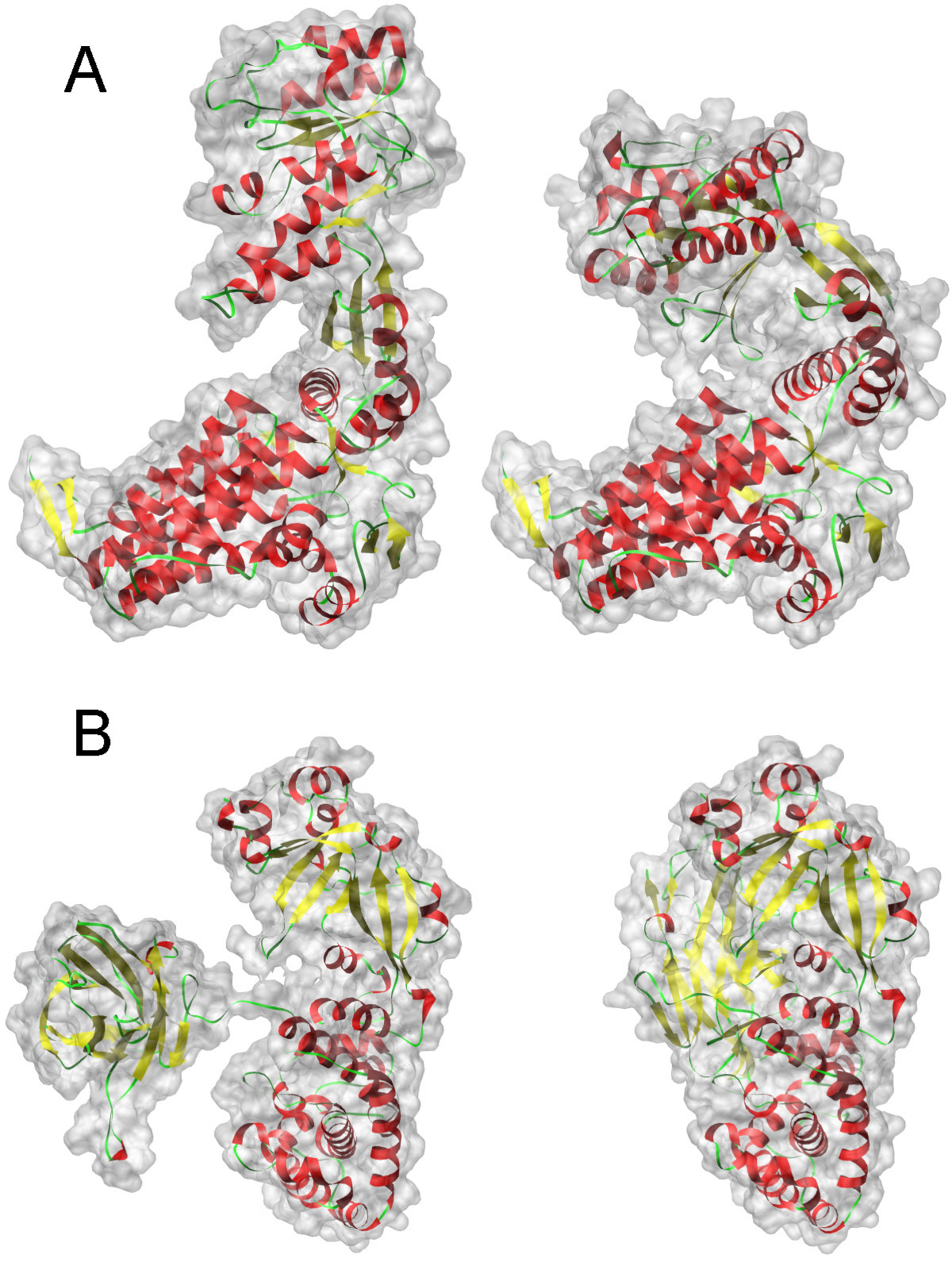
The picture shows two states of two different proteins. Functions in different states, respectively, are different
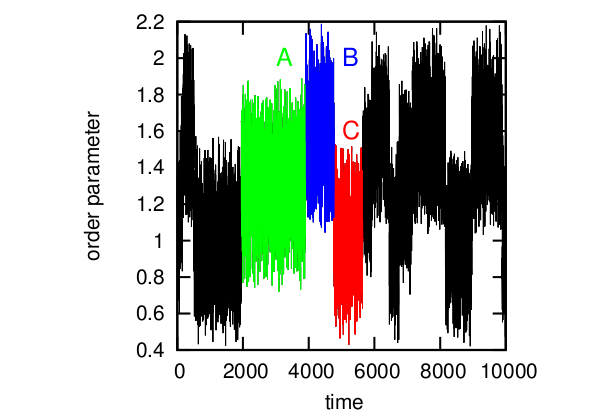
Consider the simplest example. Time series of conditional order parameter for protein. Here it is possible to distinguish three states (A, B, C), which correspond to the three states of the protein. Usually, in such cases, the formula F = -kT log (P) is used, where kT are constants, P is the state probability and F is free energy, and a free energy profile is constructed whose minima will correspond to different protein structures. And then it would seem that one can say that the system jumps between several energy holes, depending on external factors. It seems to be all right.
An example of a time series.
Profile free energy.
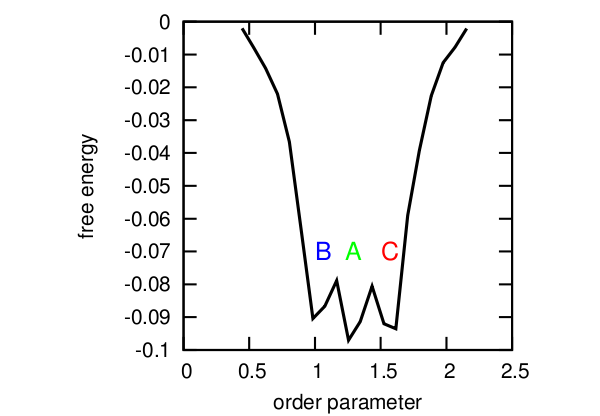
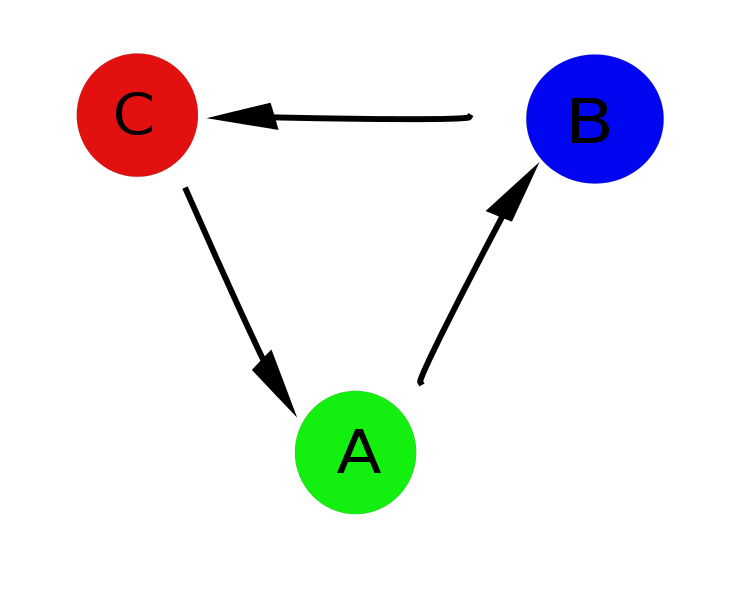
But there are several problems: the first and the most obvious is that it is not always possible to tell which parameter value corresponds to which state (for example, with OP = 1.4, all three states are possible), and the profile we obtained slightly distorts the real picture. And secondly, the fact is that in fact there is a strictly defined cycle A-> B-> C, and the transition from state A to state C is directly impossible and having all projected onto one axis as a result, we got a picture rather far from reality.
And here networks come to the rescue. You can set the correspondence between the value of the order parameter at each time point and the network node, and create a connection between the two neighboring ones with a weight equal to the conventional unit, and if during the analysis this moment is repeated, increase it accordingly. Further, as you have already guessed, we apply the clustering algorithm described above, and we get a picture that actually describes the system.
Some theory
A complex network is graphs with nontrivial topological properties. By nontrivial topological properties, we usually mean that the links between nodes of a graph are distributed according to a clever law, which in turn gives rise to various cluster structures, hubs, vulnerabilities, and so on.
The concept of a complex network grew out of the idea of tracking down citations of scientific papers in the 50s of the last century, and slowly grew, capturing the Internet, social networks, road networks and even many areas of theoretical physics, right up to quantum. The pioneer of complex networks was the Hungarian mathematician Paul Erdős, who published dozens of articles on network theory and related problems. It is curious that in his honor in the scientific community, quoting in jest began to measure Erdoch’s numbers. This is a comic metric that shows the length of the connection between Erdos and another author on the co-author's network. That is, if Vasily Pupkin is a co-author of Alfred Renyi, who in turn is co-author of Erdosh, then Vasily has Erdoch's number two (Paul and Alfred have zero and one respectively).
One of the key problems (and, as a consequence, properties) in the theory of complex networks is the problem of splitting a network into clusters. A cluster is an array of nodes that are connected to each other more than the rest of the network. Now there are dozens, if not hundreds of clustering algorithms, but all have limitations and drawbacks: either they are too slow, or the computational time increases astronomically with the number of nodes, or the accuracy suffers depending on the conditions of the initial problem. In this article, the gradient cluster algorithm will be used, the essence of which is as follows: for each node, we leave only the maximum connection with the other node (thus excluding self-communication), removing all the others. Thus, the network will be divided into subnets, which will be clusters.
')
In the upper picture, clusters are easy to find and “by eye”, and on the bottom?


Application
Why is all this necessary? The fact is that proteins under the influence of external factors (temperature, pressure, ions, water, etc.) can be in different states (conformations) that correspond to various biological functions that are not always useful. Usually states describe some parameter or several parameters (order parameter), such as radius of inertia, number of hydrogen bonds, distance between certain atoms, etc.
The picture shows two states of two different proteins. Functions in different states, respectively, are different

Consider the simplest example. Time series of conditional order parameter for protein. Here it is possible to distinguish three states (A, B, C), which correspond to the three states of the protein. Usually, in such cases, the formula F = -kT log (P) is used, where kT are constants, P is the state probability and F is free energy, and a free energy profile is constructed whose minima will correspond to different protein structures. And then it would seem that one can say that the system jumps between several energy holes, depending on external factors. It seems to be all right.
An example of a time series.

Profile free energy.

But there are several problems: the first and the most obvious is that it is not always possible to tell which parameter value corresponds to which state (for example, with OP = 1.4, all three states are possible), and the profile we obtained slightly distorts the real picture. And secondly, the fact is that in fact there is a strictly defined cycle A-> B-> C, and the transition from state A to state C is directly impossible and having all projected onto one axis as a result, we got a picture rather far from reality.
And here networks come to the rescue. You can set the correspondence between the value of the order parameter at each time point and the network node, and create a connection between the two neighboring ones with a weight equal to the conventional unit, and if during the analysis this moment is repeated, increase it accordingly. Further, as you have already guessed, we apply the clustering algorithm described above, and we get a picture that actually describes the system.

Source: https://habr.com/ru/post/182344/
All Articles