Russian Code Cup 2013 - analysis of tasks of the 3rd qualifying round

Last Sunday, the 3rd, final qualifying round of the Russian Code Cup was held. All those who wanted to take part, could come and fight for a place in the qualifying round.
Recall that the championship Russian Code Cup consists of several online tours, the results of which are selected finalists for the final competition, offline.
In total, there are 3 qualifying rounds, each of which is determined by 200 winners. Sometimes 201 people qualify for the qualifying round. This is due to the fact that the last places are equally divided by several participants who have scored an equal number of points.
')
The qualifying round winners participate in the qualifying round. In total, it turns out 600 people (or 603, if 201 people passed to qualifying rounds). After the qualifying round, 50 finalists are determined. In this case, there may also be a situation where the last place is shared by two participants. In this case, 51 people will qualify for the final.
Before the qualifying round remains about two weeks. In anticipation of the next round, we will summarize the results of the last qualifying round and analyze the problems.
Themes of the tasks:
- Task A. Exam.
- Problem B. Message.
- Problem C. Match of the Century.
- Problem D. Splitting into arrays.
- Problem E. Forest phenomenon.
During the round, logged 681 people. Of these, at least one solution was sent by 529 people.
A total of 2660 solutions were sent.
Participants who first sent solutions to the relevant tasks, and the time after the start of the round (min: s):
- Problem A : Irinka (3:59)
- Problem B : arch (5:18)
- Problem C : mr146 (19:53)
- Problem D : megaterik (37:26)
- Task E : peter50216 (78:11)
During the round, two payers were noticed. Their results were canceled immediately after the end of the round. Writing off a worker reveals a special algorithm developed by ITMO specialists and integrated into the task verification system.
The territorial distribution of participants in this round was as follows:
Russia => 337
Ukraine => 81
Belarus => 42
Kazakhstan => 18
Armenia => 10
United States => 9
Uzbekistan => 4
Switzerland => 4
Georgia => 3
Bulgaria => 2
Latvia => 2
Sweden => 2
Germany => 2
Iceland => 1
Turkmenistan => 1
Republic of Korea => 1
Ireland => 1
Macedonia => 1
Azerbaijan => 1
Romania => 1
Spain => 1
UK => 1
France => 1
Moldova => 1
Kyrgyzstan => 1
Poland => 1
Serbia => 1
200 people went to the qualifying round. The first 10 of them:
- Andrey Maksay
- Denis Mukhametyanov
- Member with username peter50216
- Victor Barinov
- Alexander Barykin
- Mikhail Roizner
- Maxim Kalinin
- Roman of Eden
- Igor Kirov
- Andrey Zayakin
The analysis of tasks, which we present below, is also available on the site of the Russian Code Cup .
Problem A. Exam
Idea: Nikolay Vedernikov
Realization: Nikolay Vedernikov
Analysis: Nikolay Vedernikov
The task
Time limit: 2 seconds
Memory limit: 256 megabytes
Igor is a good programmer, but a big slob. After losing the entire semester in computer games and watching a lot of TV shows and movies, he suddenly realized that it was time for the session to be closed so as not to fly out of the university.
The first Igor will have an exam on extreme programming. The essence of the exam is that at some time S the condition of the problem appears, which Igor has to solve before time F. The exam lasts at least a second and no more than a day. If Igor passes the task in the allotted time, then he takes the exam. If he has time to pass the task within an hour after the end of the exam, then in addition to solving the problem, he has to write testing. Otherwise, Igor collapses the exam.
Igor knows how many minutes he will write the program, and now he wants to know if he can pass the exam, or he will have to write a test, or he won't pass the exam at all.
Input Format
The first line of input contains a single integer n (1 ≤ n ≤ 104) - the number of tests. The next n lines contain S and F in the format hh: mm: ss, as well as an integer k (1 ≤ k ≤ 2000) - the start and end time of the exam and the time in minutes for which Igor will write the program.
It is guaranteed that the time in the tests is set correctly.
Output format
For each test in a separate line print the answer to the problem. If Igor passes the exam, output Perfect. If Igor has to write a test, output Test. Otherwise, output Fail.
Examples:
| Input data | Output |
| four 01:02:03 01:05:03 3 23:12:14 00:14:59 91 00:00:00 00:00:00 1000 01:00:00 05:00:00 666 | Perfect Test Perfect Fail |
Task analysis
We translate the time of the beginning and end of the exam into seconds according to the formula 60 × 60 × hh + 60 × mm + ss, as well as the time that Igor spends writing the program, according to the formula 60 × k. Then we calculate the length of the exam using the formula time exam = (time end - time start + 24 × 60 × 60)% (24 × 60 × 60), if the time exam = 0, then in fact the length of the exam is 24 × 60 × 60. If the time of writing the program is less than the duration of the exam, the answer is Perfect. If the time of writing the exam is less than the duration of the exam, increased by an hour (60 × 60 seconds), the answer is Test. Otherwise, the answer is Fail.
Task B. Message
Idea: Pavel Krotkov
Realization: Anna Malova
Analysis: Anna Malova
The task
Time limit: 2 seconds
Memory limit: 256 megabytes
After many years of unsuccessful attempts, scientists were finally able to establish a connection with a reasonable civilization in space and found out that the alphabet of aliens consists of only two letters: a and b. To receive messages, a special receiver was designed, which issues the characters a, b, as well as the special character?, If we could not make out which character was transmitted.
The analysis showed that the aliens transmit all their messages in the form of two identical lines written in a row. For example, the strings “abab” or “aaaaaa” may be alien messages, but “abba” or “aaa” may not.
The device, designed by scientists, having received a potential message of aliens as input, provides all possible ways to read a string without taking into account the above-described property. For example, having received the string “ab ??” the device outputs the strings “abaa”, “abab”, “abba” and “abbb”, of which only the string “abab” can actually be a message from aliens, and the other three cannot.
To improve the quality of the device, scientists want to know how many lines of those that are derived by the device, can not be a message of aliens. Help them do it.
Input Format
The first line contains a natural number n - the number of words in the message received by scientists.
Each of the following n lines contains a word from the message, consisting of the characters a, b, and? .. It is guaranteed that all words have an even length, and that each word has at least one? .. The total length of all words does not exceed 200,000 It is not guaranteed that there is at least one way to decipher each word as an alien message.
Output format
Print n lines. In the i-th line print the number of ways to replace? the letters a, b so that the i-th word is not a valid alien message. Since the number of methods can be very large, it is necessary to output it modulo 10 9 +7.
Examples:
| Input data | Output |
| 3 ab? b baa? abb ??? | one 2 7 |
Task analysis
Note that the answer is equal to the number of all possible messages, minus the number of tandem repeats. Let m be the number of questions in the line, and 2l the length of the line. Then the number of all possible messages is 2 m . The number of tandem repeats can be found from the following reasoning. If the position of i is a question mark, and the position of i + l a or b , then in a tandem repetition of the position of i should be the same letter. If there are question marks in both positions i and i + l, then the answer must be multiplied by two. Similarly, the situation is considered when the question mark is in the position i + l. If there are different letters in the i and i + l positions, then there are no tandem repeats for such a string.
O time (message length).
Problem C. Match of the Century
Idea: Vitaly Aksenov
Realization: Pavel Krotkov
Analysis: Pavel Krotkov
The task
Time limit: 2 seconds
Memory limit: 256 megabytes
Every year, students of the Intergalactic Physical and Theological Institute hold a “match of the century” in space football. This match lasts one day light, and players of teams from all faculties of the institute take part in it.
Before starting a match, the referee must divide all the players into two teams and assign them numbers. A total of 2n players participate in the match, of which n randomly selected players will be sent by the referee to the first team, and n remaining players to the second. After that, the judge assigns numbers to all players of both teams.
Players from both teams receive numbers, each of which is an integer from 1 to n. Numbers of all players of one team are pairwise distinct. Traditionally, in the first team, players get numbers in descending order of their growth, and in the second - in ascending order.
Students who have seen many matches of the century like to calculate the "entertainment" of each match - the sum of pairwise growth differences between players of different teams with the same numbers. So, if the first team is played by players with growth of 180 and 190 centimeters, and in the second - by players with growth of 170 and 205 centimeters, then the entertainment of this match is | 180 - 205 | + | 190 - 170 | = 45. Now it is interesting for them to calculate the mathematical expectation of the entertainment of the “match of the century,” knowing the growth of all its participants. Help them.
Input Data Format The first input line contains a positive integer t - the number of matches of the century that must be studied. The following are descriptions of the matches themselves.
The description of each match consists of two lines. The first line contains one even natural number 2n - the number of participants in the next “match of the century”. The next line contains 2n pairwise distinct natural numbers not exceeding 106 — the height of all participants.
The total number of participants in all matches that need to be studied does not exceed 106.
Input Format
The first line of input contains a positive integer t - the number of matches of the century that must be studied. The following are descriptions of the matches themselves.
The description of each match consists of two lines. The first line contains one even natural number 2n - the number of participants in the next “match of the century”. The next line contains 2n pairwise distinct natural numbers not exceeding 10 6 - the growth of all participants.
The total number of participants in all matches that need to be studied does not exceed 10 6
Output format
For each match in a separate line print one real number - the expected value. Your answer should differ from the correct one by no more than 10-6.
Examples:
| Input data | Output |
| one four 20 30 10 40 | 40.0 |
Task analysis
Let 2 × n players participate in the match. Let us number them in ascending order of growth. Now we prove the following statement: the required sum is the same for any partition by commands, and is equal to a n + 1 + a n + 2 + ... + a 2 × n - a 1 - a 2 - ... - a n . Let us reformulate: the growth of any player whose number does not exceed n is always included in the required amount with a minus sign, and the growth of a player whose number is greater than n is included in the required amount with a plus.
We will prove the statement by induction. Obviously, it holds for the case with n = 1. Now we prove the validity of the assertion for arbitrary n, under the condition of validity for n - 1. Let's look at which team got the player with the least height. If he was on the first team, he would get the number n in it. Note that the player of the second team, who received the same number, will be at least (n + 1) th in growth among all players of the match. We remove from the composition of these players, after which the task will be reduced to less. The case in which the player with the smallest height got into the second team is treated similarly.
After proving this statement, the solution of the problem becomes obvious. For example, it is possible to sort all players by height for O (n × log2n), and then take into account the first n with a minus and the rest with a plus.
Problem D. Splitting into arrays
Idea: Vitaly Aksenov
Realization: Artem Vasilyev
Analysis: Artem Vasilyev
The task
Time limit: 2 seconds
Memory limit: 256 megabytes
Consider the set of integers from 1 to 3n. It is necessary to distribute these numbers into three arrays a, b and c of length n so that for any i from 1 to n the following holds: a i + b i = c i
Input Format
The only line contains an integer n (1 ≤ n ≤ 23).
Output format
If there is no solution, in the first line print the single number −1. Otherwise, output 3 lines, each with n integers separated by spaces. The first line should contain the elements of the array a, the second - the elements of the array b, the third - the array c. Each number from 1 to 3n must be displayed exactly once.
Examples:
| Input data | Output |
| one | one 2 3 |
| 2 | -one |
Task analysis
The main idea of the solution is pre-counting and busting with clipping. First, find out for which values of n the answer does not exist. The sum of all numbers from 1 to 3n is 3n * (3n + 1) / 2. On the other hand, let us denote the sum of the elements of the array c for S. Then the sum of the elements in arrays a and b is also equal to S. We obtain that 2S = 3n * (3n + 1) / 2, that is, 3n * (3n + 1) / 2 must be divisible by 4, which is done if and only if n is comparable to 0 or 1 modulo 4. In cases where the remainder of d divided by 4 is 2 or 3, the solution is guaranteed not to exist. Under the conditions specified in the condition for all other n, a solution exists.
To speed up the brute force, heuristics and clipping should be applied. The author's solution uses the fact that under the given constraints, if there is a solution, then there is a solution in which the array a is filled with numbers from 1 to n. With this heuristic, the author's solution is able to find the answer in 3 seconds for all n from 1 to 36.
Task E. Forest Phenomenon
Idea: Vitaliy Demyanyuk
Realization: Vitaliy Demyanyuk
Analysis: Vitaly Demyanyuk
The task
Time limit: 2 seconds
Memory limit: 256 megabytes
Byteland is a very green and ecological country with many forests, rivers and lakes. All forests in Byteland have the shape of a perfect rectangle. The lengths of the sides of the i-th forest are equal to n i and m i kilometers. Each forest is divided by lines parallel to the sides of the rectangle into squares with a side length of one kilometer. Each square has its own forester.
As it is known, in the autumn each forester prepares his own firewood for the winter. But this autumn something unimaginable happened. For some unknown reason, after harvesting firewood, every forester shipped his entire supply of timber to a random, equally likely to be chosen neighbor. All foresters shipped firewood at the same time. Two foresters are called neighbors if the squares of the forest in which they live have a common side.
In order to study this phenomenon of human behavior in more detail, for each forest you need to calculate the mathematical expectation of the number of foresters who after this procedure turned out to have at least some firewood for the winter.
Input Format
The first line contains a positive integer t - the number of forests in Bytelandia.
Each of the following t lines contains two numbers n i and m i - the lengths of the sides of the i-th forest. (1 ≤ n i ≤ 10 7 , 1 ≤ m i ≤ 10 7 nm ≥ 2).
The number of forests in Byteland does not exceed 10,000.
Output format
For each forest in a separate line, print the desired expected value in the form of an irreducible fraction. The numerator and denominator must be separated by / without additional spaces. If the denominator is one, then only the numerator should be displayed.
Examples:
| Input data | Output |
| 2 13 45 | 2 2015/144 |
Task analysis
Denote one of the possible scenarios for the distribution of firewood x. We define l i, j (x) as a function that is equal to unity if a forester who lives in a square with coordinates i and j has firewood for the winter, and zero otherwise. The number of foresters who have wood for the winter is equal to the sum of l i, j (x) over all the squares of the forest. Then, by the linearity of the expectation, the required expectation is equal to the sum of the expectation values l i, j over all squares of the forest. Find the mathematical expectation l i, j : E (l i, j ) = 0 × p i, j + 1 × (1- p i, j ) = 1 - p i, j , where p i, j is the probability that the corresponding forester did not have firewood for the winter. Calculate p i, j as a product of the probabilities of events that the forester did not receive firewood from the corresponding neighbor.
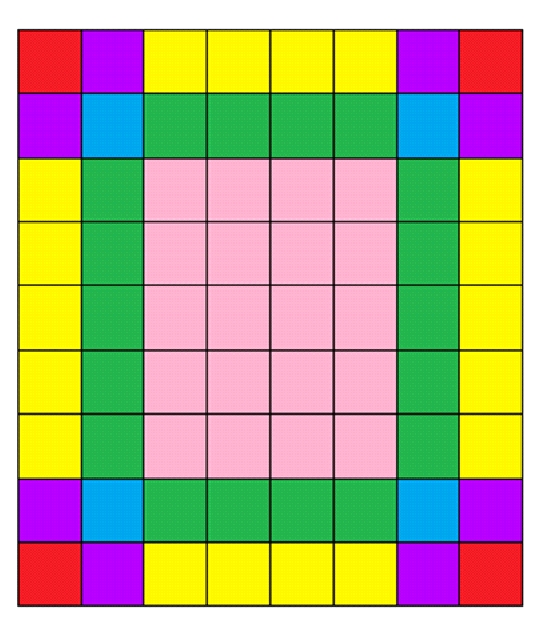
In the figure above, the squares with the same color p i, j are equal. Therefore, for each type, it is necessary to count the number of cells and multiply it by the appropriate pi, j, then add everything up. The running time of the program is O (1), since there are only six types. It is also necessary to separately consider the cases when the smaller of the parties is equal to one, two or three.
The next RCC qualifying round will be held on June 16th. Parsing tasks necessarily publish. Stay tuned!
Source: https://habr.com/ru/post/182256/
All Articles