Battleship as a recognition task
Hi, Habr!
Continuing the week of sea battle, I want to propose another way to build an optimal shooting strategy. He uses the tree view of strategy, which is quite common in game theory. The presentation of the problem as a table of solutions was borrowed from the theory of tests, which was popular in the 70s of the last century and was used, in particular, to monitor and diagnose faults in electronic circuits. This method allows you to find the optimal strategy, but it has a very large computational complexity. Alas, the game on the 10x10 field could not be analyzed.
To begin with, we will get a convenient way to present a strategy in the form of a decision tree. For example, here’s how you can shoot a cruiser and two boats on a 3x3 field.
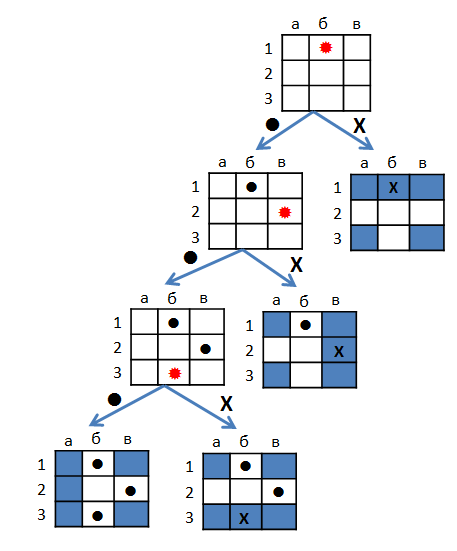
')
In the tops of the tree drawn playing field with shots already made. The current shot is marked in red. The result of the shot is attributed to the ribs: slip (.) Or hit (x). The leaves show the location of the ships. The strategy can be described in words as follows. First we shoot at b1 . If we get, it becomes clear how the ships are located, and it remains to finish them. If not, shoot at B2 . If we fall, everything is clear again. If we miss, there are two options for the location, and the shot in b3 brings final clarity.
It is clear that it is possible to describe any strategy of shooting, there would be enough paper. But in order to find a good strategy, you need to formalize what we really want. Note that the strategy describes the player’s actions “for all occasions”, but a particular game with its ship layout is described by a path in the tree from the root to one of the leaves. Having played to the end and won, we will get as many times as there were pipes on the enemy ships. You can reformulate the rules as follows: each of the players shoots until the enemy squadron is completely destroyed, and then the one who has fewer misses wins. So a good strategy is different from a bad amount of misses. And now we have two options.
You can evaluate the strategy by how many misses will be made at worst. Then, of the two strategies, the one with the maximum number of misses on the way from the root to the leaf is minimal. And we can assume that the enemy chooses the location randomly with equal probability, and try to reduce the expected number of misses. Then, of the two strategies, it will be better that the sum of the misses in all the paths from the root of each leaf of the leaf will be the smallest. For example, our strategy allows you to guaranteedly destroy ships by making no more than three misses, and the expected number of misses is (3 + 2 + 1 + 0) / 4 = 1.5.
By the way, you can try to find a strategy that will be the best in both senses. Sounds good? Alas, both tasks are too similar to the NP-difficult problem of covering the set , which promises us a lack of easy solution algorithms. But, with patience and machine time, let us try to do something.
Let's present the problem in the form of a so-called decision table. We construct a rectangular table in which the columns correspond to the cells of the playing field, and the rows correspond to all sorts of ship layout options. The table cell at the intersection of the row and column contains the “X” sign if there is a ship in this location of the ships in this cell of the playing field, and “.” otherwise. For example, here is a table describing four possible locations for a cruiser and two boats on a 3x3 field (each line to the right has a cell in which the middle of the cruiser is located — in our example, it uniquely identifies the location of ships).
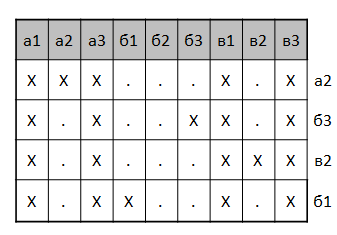
Looking at the table, it can be understood that there is no point in shooting at b2 , because there is no ship in any configuration. Shots in a1 , a3 , b1 , b3 guarantee a hit, but does not provide additional information about the location of ships. They can be performed at the beginning to intimidate the enemy. A shot at each of the remaining cells when hit unambiguously identifies the line, and when missed, reduces the number of hypotheses by one. You can think of this process as crossing out lines that contradict the accumulated information from a table.
An approximate greedy algorithm builds a tree starting at the root. The algorithm selects the column of the table (the cell for the shot), so that the proportion of rows having a ship in this cell is as close as possible to 1/2. The selected cell is assigned to the root of the tree, two edges are drawn from the root, corresponding to a slip / hit, two new vertices are suspended from the ends of the edges. Each of the new vertices gets a subtable in which lines are crossed out that contradict the results of the first shot. The same procedure is applied to each leaf until all the resulting tables contain only one row. The corresponding vertices become leaves, and the algorithm completes.
Another algorithm uses dynamic programming. It analyzes a huge graph of sub-tables, but ensures that the solution found will be optimal. Unfortunately, a detailed account of him deserves a separate post. I will somehow get together with the forces and write, but now I suggest believing in its existence and moving on to the experimental part.
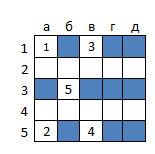
The number of configurations (1.85 * 10 15 ), voiced by the respected Mrrl , caught me in the process of writing code and pretty much cooled my ardor. Thinking, I decided to bring the matter to the end, while reducing the size of the field. The exact algorithm agreed to work with the task of firing at a squadron from one cruiser, two destroyers and three boats on a 5x5 field. The number of possible configurations in this case is only 1428, but the subtask graph consists of an impressive 10 191 257 vertices and 214 464 800 edges. The optimal algorithm allows you to destroy the squadron, allowing no more than seven misses, and on average allows 4.51 miss. The figure below shows how to determine the position of the ships with five misses (that is, when implementing the rightmost branch of the decision tree).
A greedy algorithm for the same task has built a strategy that allows 11 misses in the worst case, with an expected number of misses 5.46. The figure below shows the shooting strategy for misses (the rightmost branch of the decision tree).

The classic greedy algorithm worked badly. I think he would have done a good job of minimizing the length of the path in the tree, and the number of misses clearly requires a different empiric for choosing the cage for the shot. The exact algorithm overcame the task with half the ships at the quarter-field, so there is not much to boast about. It is a little warmer for the fact that for this small task we now know the number of misses for the optimal strategy (7 in the worst case, 4.51 on average). I would be glad if it helps colleagues building approximate algorithms.
1) The considered task is different from the classic "sea battle" in that instead of "killed" the player gives the answer "hit". The introduction of the third answer does not allow to describe the subtask only by a list of locations that are compatible with previous shots and to apply dynamic programming to the solution. I can’t imagine how to search for the optimal algorithm for a classical problem, except that it is possible to do a brute force with the exception of proven non-optimal branches.
2) The greedy algorithm, which selects the column with the maximum number of X characters at each step (i.e., which selects the cage for the shot with the highest probability of finding the ship), shows a result close to optimal: 8 misses in the worst case and 4.595 on average. The introduction of the answer “killed” significantly improves the performance: 4 misses in the worst case and 2.04 misses on average.
Thank you Mrrl for the additions.
Continuing the week of sea battle, I want to propose another way to build an optimal shooting strategy. He uses the tree view of strategy, which is quite common in game theory. The presentation of the problem as a table of solutions was borrowed from the theory of tests, which was popular in the 70s of the last century and was used, in particular, to monitor and diagnose faults in electronic circuits. This method allows you to find the optimal strategy, but it has a very large computational complexity. Alas, the game on the 10x10 field could not be analyzed.
Decision tree
And when Great Britain, and then Germany, built dreadnoughts, war between them became inevitable. Because, apart from questions about the tactics of the use of new ships, to which somehow it was possible to answer speculatively, there was one, which was theoretically impossible to answer. It sounded like this: “WHOSE DREAMS ARE BETTER?”(Free quote from the play by E. Grishkovets "Dreadnoughts")
To begin with, we will get a convenient way to present a strategy in the form of a decision tree. For example, here’s how you can shoot a cruiser and two boats on a 3x3 field.

')
In the tops of the tree drawn playing field with shots already made. The current shot is marked in red. The result of the shot is attributed to the ribs: slip (.) Or hit (x). The leaves show the location of the ships. The strategy can be described in words as follows. First we shoot at b1 . If we get, it becomes clear how the ships are located, and it remains to finish them. If not, shoot at B2 . If we fall, everything is clear again. If we miss, there are two options for the location, and the shot in b3 brings final clarity.
It is clear that it is possible to describe any strategy of shooting, there would be enough paper. But in order to find a good strategy, you need to formalize what we really want. Note that the strategy describes the player’s actions “for all occasions”, but a particular game with its ship layout is described by a path in the tree from the root to one of the leaves. Having played to the end and won, we will get as many times as there were pipes on the enemy ships. You can reformulate the rules as follows: each of the players shoots until the enemy squadron is completely destroyed, and then the one who has fewer misses wins. So a good strategy is different from a bad amount of misses. And now we have two options.
You can evaluate the strategy by how many misses will be made at worst. Then, of the two strategies, the one with the maximum number of misses on the way from the root to the leaf is minimal. And we can assume that the enemy chooses the location randomly with equal probability, and try to reduce the expected number of misses. Then, of the two strategies, it will be better that the sum of the misses in all the paths from the root of each leaf of the leaf will be the smallest. For example, our strategy allows you to guaranteedly destroy ships by making no more than three misses, and the expected number of misses is (3 + 2 + 1 + 0) / 4 = 1.5.
By the way, you can try to find a strategy that will be the best in both senses. Sounds good? Alas, both tasks are too similar to the NP-difficult problem of covering the set , which promises us a lack of easy solution algorithms. But, with patience and machine time, let us try to do something.
Decision table and strategy building algorithms
Let's present the problem in the form of a so-called decision table. We construct a rectangular table in which the columns correspond to the cells of the playing field, and the rows correspond to all sorts of ship layout options. The table cell at the intersection of the row and column contains the “X” sign if there is a ship in this location of the ships in this cell of the playing field, and “.” otherwise. For example, here is a table describing four possible locations for a cruiser and two boats on a 3x3 field (each line to the right has a cell in which the middle of the cruiser is located — in our example, it uniquely identifies the location of ships).

Looking at the table, it can be understood that there is no point in shooting at b2 , because there is no ship in any configuration. Shots in a1 , a3 , b1 , b3 guarantee a hit, but does not provide additional information about the location of ships. They can be performed at the beginning to intimidate the enemy. A shot at each of the remaining cells when hit unambiguously identifies the line, and when missed, reduces the number of hypotheses by one. You can think of this process as crossing out lines that contradict the accumulated information from a table.
An approximate greedy algorithm builds a tree starting at the root. The algorithm selects the column of the table (the cell for the shot), so that the proportion of rows having a ship in this cell is as close as possible to 1/2. The selected cell is assigned to the root of the tree, two edges are drawn from the root, corresponding to a slip / hit, two new vertices are suspended from the ends of the edges. Each of the new vertices gets a subtable in which lines are crossed out that contradict the results of the first shot. The same procedure is applied to each leaf until all the resulting tables contain only one row. The corresponding vertices become leaves, and the algorithm completes.
Another algorithm uses dynamic programming. It analyzes a huge graph of sub-tables, but ensures that the solution found will be optimal. Unfortunately, a detailed account of him deserves a separate post. I will somehow get together with the forces and write, but now I suggest believing in its existence and moving on to the experimental part.
Experiment
The theorist decides what he can, as needed, and the practitioner decides what is needed, how he can.
The number of configurations (1.85 * 10 15 ), voiced by the respected Mrrl , caught me in the process of writing code and pretty much cooled my ardor. Thinking, I decided to bring the matter to the end, while reducing the size of the field. The exact algorithm agreed to work with the task of firing at a squadron from one cruiser, two destroyers and three boats on a 5x5 field. The number of possible configurations in this case is only 1428, but the subtask graph consists of an impressive 10 191 257 vertices and 214 464 800 edges. The optimal algorithm allows you to destroy the squadron, allowing no more than seven misses, and on average allows 4.51 miss. The figure below shows how to determine the position of the ships with five misses (that is, when implementing the rightmost branch of the decision tree).

A greedy algorithm for the same task has built a strategy that allows 11 misses in the worst case, with an expected number of misses 5.46. The figure below shows the shooting strategy for misses (the rightmost branch of the decision tree).

Summary
The classic greedy algorithm worked badly. I think he would have done a good job of minimizing the length of the path in the tree, and the number of misses clearly requires a different empiric for choosing the cage for the shot. The exact algorithm overcame the task with half the ships at the quarter-field, so there is not much to boast about. It is a little warmer for the fact that for this small task we now know the number of misses for the optimal strategy (7 in the worst case, 4.51 on average). I would be glad if it helps colleagues building approximate algorithms.
Update
1) The considered task is different from the classic "sea battle" in that instead of "killed" the player gives the answer "hit". The introduction of the third answer does not allow to describe the subtask only by a list of locations that are compatible with previous shots and to apply dynamic programming to the solution. I can’t imagine how to search for the optimal algorithm for a classical problem, except that it is possible to do a brute force with the exception of proven non-optimal branches.
2) The greedy algorithm, which selects the column with the maximum number of X characters at each step (i.e., which selects the cage for the shot with the highest probability of finding the ship), shows a result close to optimal: 8 misses in the worst case and 4.595 on average. The introduction of the answer “killed” significantly improves the performance: 4 misses in the worst case and 2.04 misses on average.
Thank you Mrrl for the additions.
Source: https://habr.com/ru/post/181872/
All Articles