Elementary satellite flight simulator
I recently decided to write a satellite flight simulator around the central body. At once I will make a reservation that the satellite’s mass is negligibly small compared to the mass of the central body.

Actually the first part of the work was the study of mathematics. It was quite simple here: elementary kinematic equations were used.
Actually on this mathematical part is over.
As planned, it was planned that the user would choose the starting point himself and report the initial speed himself.
Implemented on JS through two event listeners:
The first testing was quite interesting for me, as for an astronomer))
If the orbit was very elliptical, then it precesses like this:
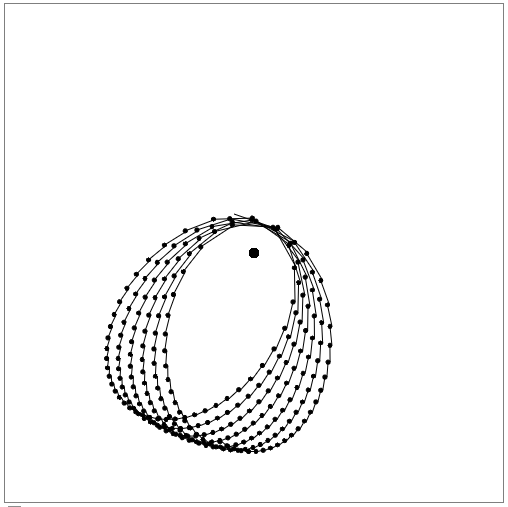
On the one hand, it was pleasant to look at such a phenomenon, but on the other hand, I understood that the matter was not in precession, but in inaccurate calculation of the position, because sometimes there were such orbits:
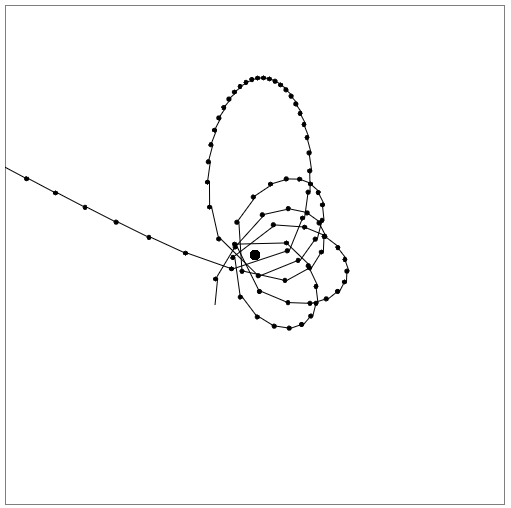
In fact, the problem turned out to be simple: ideally, the animation should be time-differentiated, that is, it should be divided into such small time steps that the speed and its direction did not have time to change much. And we set a constant time step, and if this step was quite enough to calculate the satellite position in the aphelion, then it should be several times less in the overcrowding. For this, the floating position calculation step was made, while the rendering step remained constant.
Implementation:
For debugging, I made a radius-vector of the satellite, which helps to understand where it is when the satellite flew out of the picture:
Everything is here: http://astrokot.ru/planetarium/vectors.html

Actually the first part of the work was the study of mathematics. It was quite simple here: elementary kinematic equations were used.
/* t - G - ( ) msun - ( ) */ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); // - var gs=G*msun/r2; // , // var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2); var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); // vx+=ivx/t; vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy) // /* */ xc+=vx*t; yc+=vy*t; Actually on this mathematical part is over.
Interface
As planned, it was planned that the user would choose the starting point himself and report the initial speed himself.
Implemented on JS through two event listeners:
var xc,yc,xc2,yc2,intervalID,vx,vy; /* */ cnv.addEventListener('mousedown',function (event) { /* */ xc=event.offsetX; yc=event.offsetY; /* */ clearInterval(intervalID) }, false) /* , */ cnv.addEventListener('mouseup',function (event) { /* */ clearInterval(intervalID) /* */ xc2=event.offsetX; yc2=event.offsetY; /* */ vx=(-xc+xc2)*0.4 /* */ vy=(-yc+yc2)*0.4 intervalID=setInterval(dodo,70); }, false) Testing
The first testing was quite interesting for me, as for an astronomer))
If the orbit was very elliptical, then it precesses like this:

On the one hand, it was pleasant to look at such a phenomenon, but on the other hand, I understood that the matter was not in precession, but in inaccurate calculation of the position, because sometimes there were such orbits:

In fact, the problem turned out to be simple: ideally, the animation should be time-differentiated, that is, it should be divided into such small time steps that the speed and its direction did not have time to change much. And we set a constant time step, and if this step was quite enough to calculate the satellite position in the aphelion, then it should be several times less in the overcrowding. For this, the floating position calculation step was made, while the rendering step remained constant.
Implementation:
var i=0; do{ var r2=(xsun-xc)*(xsun-xc)+(ysun-yc)*(ysun-yc); var gs=G*msun/r2; var ivx=(t*t*gs/2)*(xsun-xc)/Math.sqrt(r2); var ivy=(t*t*gs/2)*(ysun-yc)/Math.sqrt(r2); vx+=ivx/t; vy+=ivy/t; var V=Math.sqrt(vx*vx+vy*vy) xc+=vx*t; yc+=vy*t; i++ }while(i<=1/t) Fine-tuning
For debugging, I made a radius-vector of the satellite, which helps to understand where it is when the satellite flew out of the picture:
ctx.moveTo(xc,yc) ctx.lineTo(xsun,ysun) ctx.stroke() Everything is here: http://astrokot.ru/planetarium/vectors.html
')
Source: https://habr.com/ru/post/181664/
All Articles