Generate 3D grids with predefined surface regions using NetGen
Introduction
In a previous post, we looked at the features of using third-party open source libraries Freefem ++ and NetGen in an aerodynamic process modeling program. It was about the possibility of including these libraries in a commercial project from a licensing point of view, about the features of the performance of functions and inclusion in the software architecture. This article is an addition to the previous one, in which we take a closer look at the NetGen library. Of interest are the functions of generating a 3D finite element mesh with specified regions on the model surface.
NetGen connection in MS Visual Studio
We show how you can connect NetGen to a C ++ program. From the official site of the project NetGen download archive. In our case, NetGen version 4.9.13 was available. To connect the library, you need three folders from the archive: libsrc, nglib, windows. In Visual Studio, we create a project and solution for the demo program and include the existing nglib.vcxproj project file from the windows folder. Since in our experiment the nglib project was created in an earlier version of Visual Studio, we are simultaneously converting the project to a new version. In the nglib project settings, add the libsrc \ include include folder, add the NO_PARALLEL_THREADS symbol, remove pthreadVC2.lib from the additional linker dependencies, delete the linker post event, and set up the target folders so that the project is assembled without errors.
The inclusion of the nglib.h header file should be recorded in the following not very familiar way:
namespace nglib
{
#include "nglib.h"
}
using namespace nglib; Test model
The space that must be filled with finite elements can be defined for NetGen in two ways:
- In the form of constructive block geometry operators (CSG).
- In the form of a description of the boundary of space in the file format STL.
Here we consider only the second variant of the surface description - the description of the three-dimensional model in the text format STL. The graphic image of the test model is shown in Fig. 1. The model is a parallelepiped of 10 X 10 X 5. On one of the faces there is a rectangular region of 5 X 2 with an offset (4; 2), the boundaries of which must remain unchanged
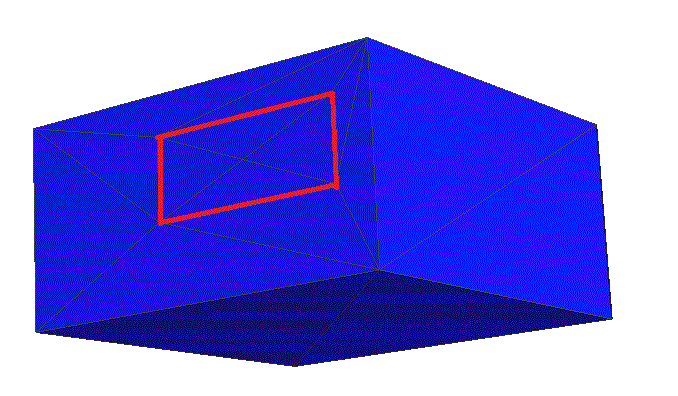
Fig. 1. Surface triangulation to form an STL file. Red color indicates the region, the boundaries of which should remain unchanged.
')
Below is the contents of the STL file describing the test model:
solid facet normal 1 0 0 outer loop vertex 10 4 2 vertex 10 6.5 3 vertex 10 4 4 endloop endfacet facet normal 1 0 0 outer loop vertex 10 6.5 3 vertex 10 9 4 vertex 10 4 4 endloop endfacet facet normal 1 0 0 outer loop vertex 10 9 2 vertex 10 6.5 3 vertex 10 4 2 endloop endfacet facet normal 1 0 0 outer loop vertex 10 9 2 vertex 10 9 4 vertex 10 6.5 3 endloop endfacet facet normal 1 0 0 outer loop vertex 10 0 5 vertex 10 0 0 vertex 10 4 2 endloop endfacet facet normal 1 0 0 outer loop vertex 10 4 2 vertex 10 4 4 vertex 10 0 5 endloop endfacet facet normal 1 0 0 outer loop vertex 10 10 5 vertex 10 0 5 vertex 10 4 4 endloop endfacet facet normal 1 0 0 outer loop vertex 10 9 4 vertex 10 10 5 vertex 10 4 4 endloop endfacet facet normal 1 0 0 outer loop vertex 10 9 2 vertex 10 10 5 vertex 10 9 4 endloop endfacet facet normal 1 0 0 outer loop vertex 10 10 0 vertex 10 10 5 vertex 10 9 2 endloop endfacet facet normal 1 0 0 outer loop vertex 10 10 0 vertex 10 9 2 vertex 10 4 2 endloop endfacet facet normal 1 0 0 outer loop vertex 10 10 0 vertex 10 4 2 vertex 10 0 0 endloop endfacet facet normal -1 0 0 outer loop vertex 0 10 5 vertex 0 10 0 vertex 0 0 5 endloop endfacet facet normal -1 0 0 outer loop vertex 0 0 0 vertex 0 0 5 vertex 0 10 0 endloop endfacet facet normal 0 -1 0 outer loop vertex 0 0 5 vertex 0 0 0 vertex 10 0 5 endloop endfacet facet normal 0 -1 0 outer loop vertex 10 0 0 vertex 10 0 5 vertex 0 0 0 endloop endfacet facet normal 0 1 0 outer loop vertex 10 10 5 vertex 10 10 0 vertex 0 10 5 endloop endfacet facet normal 0 1 0 outer loop vertex 0 10 0 vertex 0 10 5 vertex 10 10 0 endloop endfacet facet normal 0 0 1 outer loop vertex 0 0 5 vertex 10 0 5 vertex 0 10 5 endloop endfacet facet normal 0 0 1 outer loop vertex 10 10 5 vertex 0 10 5 vertex 10 0 5 endloop endfacet facet normal 0 0 -1 outer loop vertex 10 0 0 vertex 0 0 0 vertex 10 10 0 endloop endfacet facet normal 0 0 -1 outer loop vertex 0 10 0 vertex 10 10 0 vertex 0 0 0 endloop endfacet endsolid
The information in the STL file has the following format. At the beginning and end of the file the keywords solid and endsolid are specified, between which are listed the triangles defining the required surface in the format:
facet normal nx ny nz outer loop vertex v1x v1y v1z vertex v2x v2y v2z vertex v3x v3y v3z endloop endfacetwhere nx, ny, nz are the components of the normal vector along the X, Y, Z axes, directed outward from the simulated object; (v1x, v1y, v1z), (v2x, v2y, v2z), (v3x, v3y, v3z) are the coordinates of the three vertices of the triangle.
An example of a program that generates a finite element mesh
Below is the text of the program that performs all the actions necessary to obtain a finite element mesh. This program reads the OneRegionBar.stl STL file and writes the finite element mesh to the OneRegionBar.vol file.
#include "stdafx.h"
#include <iostream>
#include <fstream>
namespace nglib
{
#include ".. \ NetGen \ nglib \ nglib.h"
}
using namespace std;
using namespace nglib;
void main ()
{
const char * stlFileName = ".. \\ Data \\ OneRegionBar.stl";
const char * volFileName = ".. \\ Data \\ OneRegionBar.vol";
// Edges on the surface
const int EDGES_NUM = 4;
const int POINTS_NUM = 4;
typedef double Point [3];
Point points [POINTS_NUM] = {{10, 4, 2}, {10, 9, 2}, {10, 9, 4}, {10, 4, 4}};
typedef pair <int, int> Edge;
Edge edges [EDGES_NUM] = {Edge (0,1), Edge (1, 2), Edge (2,3), Edge (3, 0)};
// Grid generation parameters
Ng_Meshing_Parameters ngMeshParameters;
ngMeshParameters.maxh = 10;
ngMeshParameters.fineness = 0.4;
ngMeshParameters.secondorder = 0;
ngMeshParameters.quad_dominated = 0;
ngMeshParameters.grading = 0.0;
ngMeshParameters.optsurfmeshenable = false;
ngMeshParameters.optsteps_2d = 0;
ngMeshParameters.closeedgeenable = false;
// The result of the operations
Ng_Result ng_res;
//
// Start grid building
//
// Reading the STL file, creating the object "STL-geometry"
Ng_STL_Geometry * stlGeometry = Ng_STL_LoadGeometry (stlFileName);
// Adding unchangeable edges to the "geometry"
for (int i = 0; i <EDGES_NUM; i ++)
{
double * p1 = points [edges [i] .first];
double * p2 = points [edges [i] .second];
Ng_STL_AddEdge (stlGeometry, p1, p2);
}
// Initialize an object with an STL description
ng_res = Ng_STL_InitSTLGeometry (stlGeometry);
if (ng_res! = NG_OK)
{
cout << "Error in Ng_STL_InitSTLGeometry" << endl;
}
// For now, an empty element mesh object
Ng_Mesh * mesh = Ng_NewMesh ();
// Build edges on model surface
ng_res = Ng_STL_MakeEdges (stlGeometry, mesh, & ngMeshParameters);
if (ng_res! = NG_OK)
{
cout << "Error in Ng_STL_MakeEdges" << endl;
}
// Generate space surface
ng_res = Ng_STL_GenerateSurfaceMesh (stlGeometry, mesh, & ngMeshParameters);
if (ng_res! = NG_OK)
{
cout << "Error in Ng_STL_GenerateSurfaceMesh" << endl;
}
// Generate Finite Element Network
ng_res = Ng_GenerateVolumeMesh (mesh, & ngMeshParameters);
if (ng_res! = NG_OK)
{
cout << "Error in Ng_GenerateVolumeMesh" << endl;
}
// Save Finite Element Mesh To File
Ng_SaveMesh (mesh, volFileName);
} Next we give detailed comments on the program text:
- The coordinates of the points that are the edges of the edges are in the points [POINTS_NUM] array. In the array of edges [EDGES_NUM], the edges of the surface region are specified as the corresponding pairs of point numbers. These edges will need to be specified by NetGen so that they remain on the surface of the model.
- The grid generation process is controlled using parameters collected in the ngMeshParameters object of the Ng_Meshing_Parameters class. One of the parameters - maxh limits the maximum size of the grid elements. With the help of other parameters, you can fine-tune the generation process: limit the minimum size of elements, initiate grid optimization, etc.
- The STL file is read by the Ng_STL_LoadGeometry () function, and the STL geometry object is returned:
Ng_STL_Geometry * stlGeometry = Ng_STL_LoadGeometry (stlFileName);where Ng_STL_Geometry should be understood as a type of pointer to an object with an STL geometry. In fact, Ng_STL_Geometry, like some other types, is a synonym for void *. NetGen authors in this way completely hid the features of the implementation of complex objects. - Next, you need to add edges to the STL geometry object. They are added in a loop using the Ng_STL_AddEdge () function:
Ng_STL_AddEdge (stlGeometry, p1, p2);where stlGeometry is an STL geometry object; p1 and p2 are edge vertices. Each vertex is specified by an array of components along the X, Y, Z axes. These vertices are selected from the edge array of edges that was previously formed. - Call the Ng_STL_InitSTLGeometry () function to initialize the STL geometry object:
ng_res = Ng_STL_InitSTLGeometry (stlGeometry); - Create an empty mesh item object pointed to by mesh. For this, the Ng_NewMesh () function is executed:
Ng_Mesh * mesh = Ng_NewMesh (); - To form edges on the surface of the model in accordance with the STL-geometry and generation parameters:
ng_res = Ng_STL_MakeEdges (stlGeometry, mesh, & ngMeshParameters); - Triangulate the model surface with the Ng_STL_GenerateSurfaceMesh () function. Here previously specified edges are taken into account, which will remain undistorted, and generation parameters will be taken into account:
ng_res = Ng_STL_GenerateSurfaceMesh (stlGeometry, mesh, & ngMeshParameters); - And, finally, the generation of the grid of elements is performed directly with the Ng_GenerateVolumeMesh () function, taking into account the generation parameters:
ng_res = Ng_GenerateVolumeMesh (mesh, & ngMeshParameters); - In this program, the result of the grid generation is output to the VOL file using the Ng_SaveMesh () function, which is passed a pointer to the grid and the file name:
Ng_SaveMesh (mesh, volFileName);
Mesh generation result
The result of the grid generation is a program object under the Ng_Mesh pointer, in the demonstration program it is a mesh pointer. There is a set of functions that provide programmatic access to the properties of the mesh of elements: get the number of points in the grid Ng_GetNP (), get the number of triangles on the surface Ng_GetNSE (), get the number of finite elements Ng_GetNE (), get the coordinates of the point Ng_GetPoint (), get the element of the surface Ng_GetSurfaceElement ( ), get the final element of Ng_GetVolumeElement (), save the grid to the Ng_SaveMesh file.
A VOL file saved in the program can be opened in the netgen.exe visualizer. The result of viewing the file is shown in Fig. 2. As can be seen in the figure, the boundaries of the surface region remained unchanged.
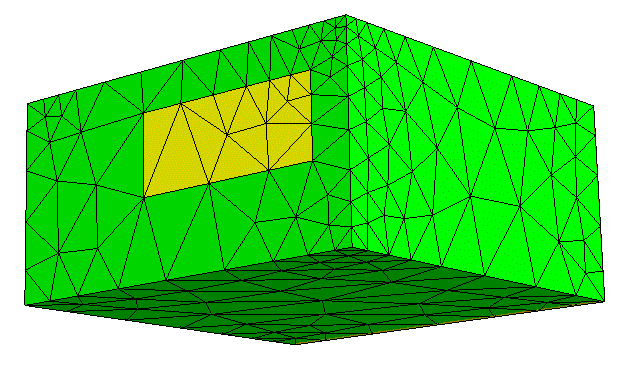
Fig. 2. The surface of the model after generating a grid of elements
The .vol file generated by NetGen has the following format:
- At the beginning of the file, the format code (mesh3d), model dimension (dimension 3), geometry code (geomtype 0) are indicated:
mesh3d dimension 3 geomtype 0
- Next, after the surfaceelements keyword, the quantity is indicated and surface elements are listed. For each element, the number of the surface, the number of the “material” of the surface, the reserved integer field, the number of points that describe the surface element (for triangles - 3), the numbers of three points of the surface element vertices are recorded. Hereinafter points are numbered from 1.
# surfnr bcnr domin domout np p1 p2 p3 surfaceelements 546 2 1 1 0 3 3 4 13 2 1 1 0 3 4 5 107 # ... - The file lists the final elements, for each of which the number of “material” is recorded, the number of vertices of one element (for tetrahedra there are four) and the number of points that are vertices:
# matnr np p1 p2 p3 p4 volumeelements 1009 1 4 213 85 153 214 1 4 298 307 301 305 # ... - Specifies information about the edges on the surface:
# surfid 0 p1 p2 trignum1 trignum2 domin / surfnr1 domout / surfnr2 ednr1 dist1 ednr2 dist2 edgesegmentsgi2 220 1 0 1 2 1 1 0 0 1 0 1 2 2 0 2 1 6 6 0 0 1 2 1 0 # ... - Lists points that are grid nodes:
# XYZ points 333 10.00000000000000 4.0000000000000000 4.0000000000000000 10.00000000000000 4.00000000000000 2.0000000000000000 # ... - At the end of the file, color components are recorded for surfaces identified by numbers. These colors are used by the visualizer to color the surface. Here for the surface with number 2 the color is set so as to select a rectangular region in Fig. 2
# Surfnr Red Green Blue face_colours 7 2 1.00000000 1.00000000 0.00000000 3 0.00000000 1.00000000 0.00000000 # ...
2D grid generation with NetGen
NetGen has a feature for creating 2D mesh elements. In the particular case, this function can be useful, for example, for generating an STL file for a 3D model that has flat edges. The geometry of the model is described in the input file in the form of the boundaries of areas of space. The boundaries of the subdomains of a partition are specified either by using straight line segments or by using quadratic splines. When describing a border, it is necessary to indicate the area number to the left and right of the border. The area outside the grid is encoded by the number 0.

Fig. 3. Coding of points and areas for generating 2D mesh of elements
We give an example of the input file corresponding to Fig. 3
splinecurves2dv2 2 points 100 2 3 0 3 3 2 4 0 2 5 1 0 6 2 0 7 2 1 8 1 1 segments 1 0 2 1 5 -bc = 1 2 0 2 5 6 -bc = 1 1 0 2 6 2 -bc = 1 1 0 2 2 3 -bc = 1 1 0 2 3 4 -bc = 1 1 0 2 4 1 -bc = 1 2 1 2 6 7 -bc = 1 2 1 2 7 8 -bc = 1 2 1 2 8 5 -bc = 1 materials 1 domain1 -maxh = 1 2 domain2 -maxh = 1
At the beginning of this file is the splinecurves2dv2 keyword. Behind it is the grid rebuilding factor (here - 2). After the keyword points, the model description points are listed: point number and coordinates along the X, Y axes.
Next, after the segments keyword, there is a list of border segments in the following format:
- The area number to the left of the border.
- The area number to the right of the border.
- The number of points to describe the border segment (in example 2).
- The number of the starting point of the boundary.
- The number of the end point of the boundary.
- Generation control flags. The bc flag (the number of the boundary condition) has to be specified even when it is not used.
After the keyword materials, areas ("materials") are listed in the following format:
- The area number.
- The name of the material.
- Generation control flags. Here the maxh flag can be specified, limiting the maximum size of the mesh elements.
Below is a program that generates a 2D mesh:
#include "stdafx.h"
namespace nglib
{
#include ".. \ NetGen \ nglib \ nglib.h"
}
using namespace nglib;
void main () {
const char * in2DFileName = ".. \\ Data \\ triangulation.in2d";
const char * volFileName = ".. \\ Data \\ triangulation.vol";
Ng_Geometry_2D * geom;
Ng_Init ();
geom = Ng_LoadGeometry_2D (in2DFileName);
Ng_Meshing_Parameters mp;
mp.maxh = 10,000;
mp.fineness = 1;
mp.secondorder = 0;
Ng_Mesh * mesh;
Ng_GenerateMesh_2D (geom, & mesh, & mp);
Ng_SaveMesh (mesh, volFileName);
}
To generate a 2D mesh, the object is used to describe the 2D geometry by the pointer geom. The result of the mesh generation is in the object by the mesh pointer. In the example, the same Ng_SaveMesh () function is used to display the result of the generation as in the example of generating the 3D grid. Therefore, in this case, the output file has a structure for the 3D grid, but the value of the Z coordinate in it is everywhere zero. The program interface for working with 2D mesh contains the functions Ng_GetNP_2D () - get the number of grid nodes, Ng_GetNE_2D () - get the number of elements in the grid, Ng_GetPoint_2D () - get the coordinates of the grid node by the node number, Ng_GetElement_2D () - get the coordinates of the nodes of the element by item number. The visualization of the 2D grid generation result is shown in Fig. 4. As can be seen from the figure, the borders of the region are not distorted.
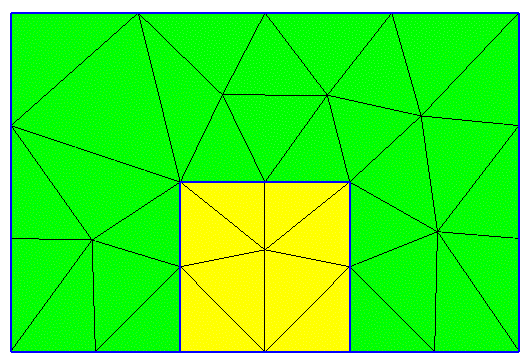
Fig. 4. The result of the generation of 2D grids
Conclusion
This article provides a brief presentation of NetGen, from which it follows that this library can be conveniently used in applications that require the generation of a 3D mesh of elements. Library functions can be studied and used without writing code. NetGen comes with a netgen.exe application that implements a visual interface to all library functions. Figures in this article, depicting the grid elements, obtained using this application.
Source: https://habr.com/ru/post/181616/
All Articles