Using artificial immune systems to solve symbolic regression
Good day, dear habro-community!
I submit to your judgment an article written based on my master's work (Faculty of Applied Mathematics, Computer Science and Mechanics of the Voronezh State University). Her theme is "The use of distributed artificial immune systems to solve the problem of symbolic regression." I will try briefly (but informatively) to review the basic concepts of artificial immune systems and my approach to their implementation for solving the problem of symbolic regression - restoring the symbolic representation of a function from a given set of its values at some points. The program was written in Python (version 3.3), the source code is available on Github.
The search showed that the topic of artificial immune systems in Habré is covered very sparingly ( times ). And in Russian, only one book is worthy of mentioning, which is almost impossible to find in the printed version [1]. Therefore, we consider some basic concepts borrowed from biology.
In some ways, immune systems can be considered heirs of genetic algorithms and neural networks with specific characteristics. Judging from various publications, they are trying to apply them for the following tasks: recognition (along with the immune systems), creation of antiviruses (which is logical, based on the basic function of biological immune systems), various optimization tasks.
Lymphocytes are the cells that make up the immune system. In the body, there are B-lymphocytes, which are both the main carriers of immune memory, and the main “combat units” that provide resistance to the enemy (antigen), and T-lymphocytes, which can enhance or suppress the B-cell response. In the overwhelming majority of papers, only B-lymphocytes are considered, we will also consider only them. It is obvious that, depending on the problem being solved, lymphocytes can be different objects of the considered area. In our task (searching for a symbolic representation of a function), the lymphocyte will be one of the possible solutions to the problem — a certain function represented by an expression tree (for example, such as in Figure 1). In this tree, various operations can be used (+, -, *, /, sin, cos), numbers, variables, the maximum number of which is set (to limit the search depth). If you use the terms of genetic algorithms, a lymphocyte is just an individual.
')
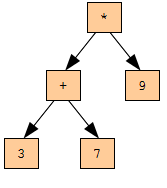 Fig. one
Fig. one
Affinity is a measure of how well a given lymphocyte responds to an antigen (virus). In biology, this is determined by various chemical bonds and reactions; in our country, this is simply the value of the objective function, which is the Euclidean distance between the exact given values of the function and the values of the function obtained at the same points.
Initially, a number of randomly generated lymphocytes are created (in the body, the bone marrow is involved). Then, throughout the entire system functioning cycle, the best of the current set of lymphocytes are selected, various hypermutation operations are applied to them (to create better adapted cells — evolution in action). Then, from the old and newly obtained cells, a new current set is selected, and this step is repeated anew until a solution is found with sufficient accuracy, or we carry out the maximum allowable number of iterations. As an assessment of solutions, the previously considered objective function is used. The functioning algorithm can be observed in Figure 2.
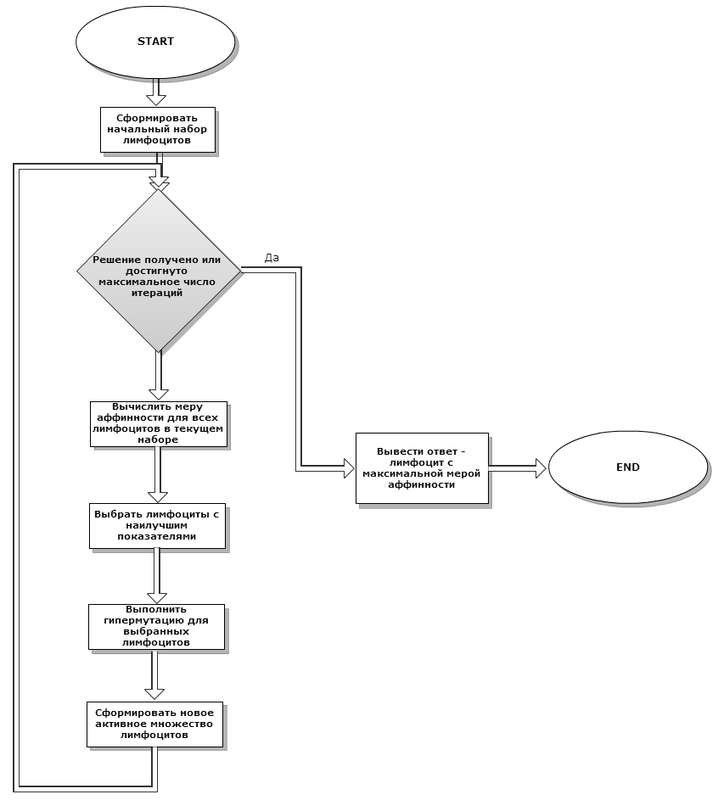 Fig. 2
Fig. 2
It is easy to see that the algorithm is similar to the classical genetic one, only the recombination operators are not used here, and the selection looks different (similar to elitism, in fact).
The following actions on expression trees are used as mutations:
Of course, I would like to add the ability to parallelize this system for functioning on several machines. In this case, OpenMP had to be abandoned for precisely this reason (it is necessary to run on several machines), MPI - on another: I would like the compute nodes to be added / fail / shut down while the entire system is running, and the system continued would function. This can be achieved by creating such a “topology”, which is used in p2p. One node knows about several neighbors, exchanges only with them. Of course, it looks like a bicycle, but to check the very possibility of paralleling this model - just right.
It now remains to figure out how to organize this most distributed immune system, given that data transmission over the network is not very fast, so the interaction between the nodes at each iteration is excluded. The biological immune system can be considered distributed (to some extent) - cells are distributed throughout the body. Therefore, in our model, you can simply add the exchange of the best lymphocytes between two nodes every N iterations. And, of course, not with the same thing, but with different ones. Thus, the parallel version of our algorithm will take the following form:
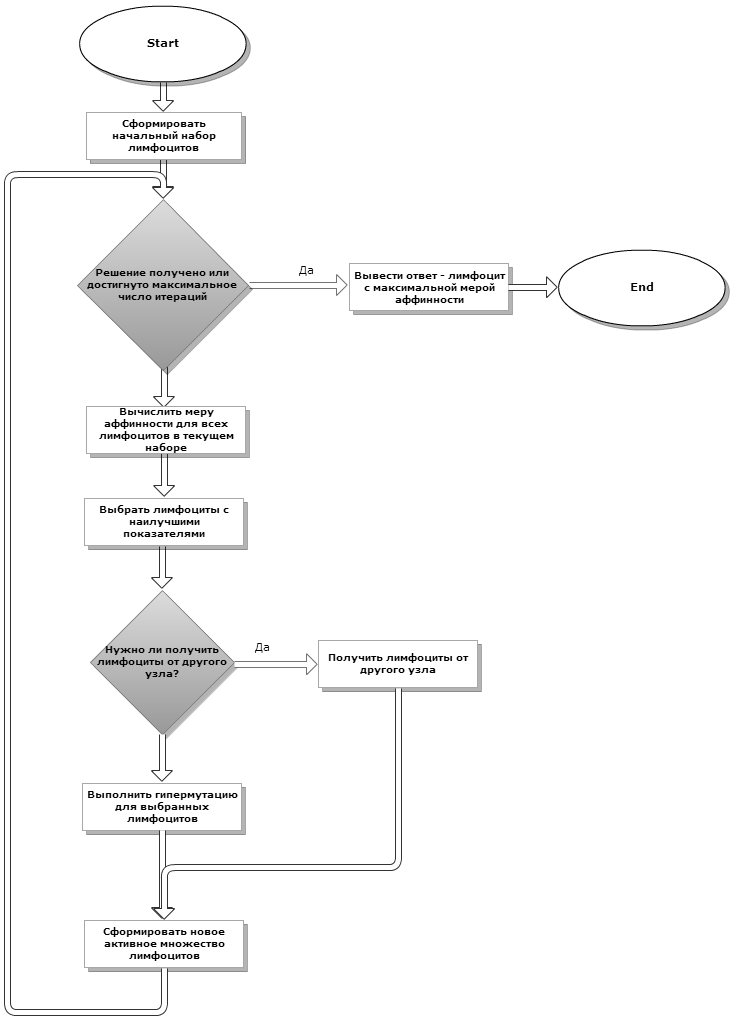 Fig. 3
Fig. 3
If we draw analogies with genetic algorithms, then such distribution is similar to the island model - when individual populations exchange specially selected individuals.
I am not a Python programmer (but very much C #), but Python is close to me and I really like it, I handed in tasks for numerical methods (thanks to numpy, scipy, matplotlib), wrote scripts for myself. I read a couple of books (Lutz, Dive into python), PEP-8, of course, but I think that the code for good Python programmers does not look very appetizing. By the time it came out about as much as I would write it in C #. I used unittest, for testing there are scripts main.py, local_node.py and local_server.py. All comments / additions / tips are very welcome, I would like to get at least some feedback.
Project on Github
This is how the program works (for the function x * x + sin (sin (x)) * x * y, the function values are given at 100 points, 4 computing nodes, 200 iterations of the algorithm, exchange after every 30 iterations):
 Fig. four
Fig. four
1) Artificial immune systems and their application / [ed. Dasgupta] - M .: Fizmatlit 2006 - 344 p.
2) Colin G. Johnson Artificial Immune Systems Programming for Symbolic Regression / Colin G. Johnson // Genetic Programming: 6th European Conference. - 2003. - P. 345–353 - ISBN = 3-540-00971-X
PS Sorry if the text is a bit muddled, in some way it is an attempt to prepare for defense - to collect thoughts, to tell about the work done.
I submit to your judgment an article written based on my master's work (Faculty of Applied Mathematics, Computer Science and Mechanics of the Voronezh State University). Her theme is "The use of distributed artificial immune systems to solve the problem of symbolic regression." I will try briefly (but informatively) to review the basic concepts of artificial immune systems and my approach to their implementation for solving the problem of symbolic regression - restoring the symbolic representation of a function from a given set of its values at some points. The program was written in Python (version 3.3), the source code is available on Github.
Basic concepts and description of the immune system
The search showed that the topic of artificial immune systems in Habré is covered very sparingly ( times ). And in Russian, only one book is worthy of mentioning, which is almost impossible to find in the printed version [1]. Therefore, we consider some basic concepts borrowed from biology.
In some ways, immune systems can be considered heirs of genetic algorithms and neural networks with specific characteristics. Judging from various publications, they are trying to apply them for the following tasks: recognition (along with the immune systems), creation of antiviruses (which is logical, based on the basic function of biological immune systems), various optimization tasks.
Lymphocytes are the cells that make up the immune system. In the body, there are B-lymphocytes, which are both the main carriers of immune memory, and the main “combat units” that provide resistance to the enemy (antigen), and T-lymphocytes, which can enhance or suppress the B-cell response. In the overwhelming majority of papers, only B-lymphocytes are considered, we will also consider only them. It is obvious that, depending on the problem being solved, lymphocytes can be different objects of the considered area. In our task (searching for a symbolic representation of a function), the lymphocyte will be one of the possible solutions to the problem — a certain function represented by an expression tree (for example, such as in Figure 1). In this tree, various operations can be used (+, -, *, /, sin, cos), numbers, variables, the maximum number of which is set (to limit the search depth). If you use the terms of genetic algorithms, a lymphocyte is just an individual.
')
 Fig. one
Fig. oneAffinity is a measure of how well a given lymphocyte responds to an antigen (virus). In biology, this is determined by various chemical bonds and reactions; in our country, this is simply the value of the objective function, which is the Euclidean distance between the exact given values of the function and the values of the function obtained at the same points.
Initially, a number of randomly generated lymphocytes are created (in the body, the bone marrow is involved). Then, throughout the entire system functioning cycle, the best of the current set of lymphocytes are selected, various hypermutation operations are applied to them (to create better adapted cells — evolution in action). Then, from the old and newly obtained cells, a new current set is selected, and this step is repeated anew until a solution is found with sufficient accuracy, or we carry out the maximum allowable number of iterations. As an assessment of solutions, the previously considered objective function is used. The functioning algorithm can be observed in Figure 2.
 Fig. 2
Fig. 2It is easy to see that the algorithm is similar to the classical genetic one, only the recombination operators are not used here, and the selection looks different (similar to elitism, in fact).
The following actions on expression trees are used as mutations:
- Mutation of the numeric value 2 * x → 2.23 * x
- Mutation of the variable 2 * (x + y) * x → 2 * (x + y) * y
- Mutation of the unary operator sin (x) * y → cos (x) * y
- Mutation of the binary operator x + y → xy
- Mutation of a subexpression (subtree of an expression tree) 2 * (x + y) → 2 * sin (x)
Add concurrency
Of course, I would like to add the ability to parallelize this system for functioning on several machines. In this case, OpenMP had to be abandoned for precisely this reason (it is necessary to run on several machines), MPI - on another: I would like the compute nodes to be added / fail / shut down while the entire system is running, and the system continued would function. This can be achieved by creating such a “topology”, which is used in p2p. One node knows about several neighbors, exchanges only with them. Of course, it looks like a bicycle, but to check the very possibility of paralleling this model - just right.
It now remains to figure out how to organize this most distributed immune system, given that data transmission over the network is not very fast, so the interaction between the nodes at each iteration is excluded. The biological immune system can be considered distributed (to some extent) - cells are distributed throughout the body. Therefore, in our model, you can simply add the exchange of the best lymphocytes between two nodes every N iterations. And, of course, not with the same thing, but with different ones. Thus, the parallel version of our algorithm will take the following form:
 Fig. 3
Fig. 3If we draw analogies with genetic algorithms, then such distribution is similar to the island model - when individual populations exchange specially selected individuals.
Implementation and code
I am not a Python programmer (but very much C #), but Python is close to me and I really like it, I handed in tasks for numerical methods (thanks to numpy, scipy, matplotlib), wrote scripts for myself. I read a couple of books (Lutz, Dive into python), PEP-8, of course, but I think that the code for good Python programmers does not look very appetizing. By the time it came out about as much as I would write it in C #. I used unittest, for testing there are scripts main.py, local_node.py and local_server.py. All comments / additions / tips are very welcome, I would like to get at least some feedback.
Project on Github
This is how the program works (for the function x * x + sin (sin (x)) * x * y, the function values are given at 100 points, 4 computing nodes, 200 iterations of the algorithm, exchange after every 30 iterations):
 Fig. four
Fig. fourLiterature and links
1) Artificial immune systems and their application / [ed. Dasgupta] - M .: Fizmatlit 2006 - 344 p.
2) Colin G. Johnson Artificial Immune Systems Programming for Symbolic Regression / Colin G. Johnson // Genetic Programming: 6th European Conference. - 2003. - P. 345–353 - ISBN = 3-540-00971-X
PS Sorry if the text is a bit muddled, in some way it is an attempt to prepare for defense - to collect thoughts, to tell about the work done.
Source: https://habr.com/ru/post/181342/
All Articles