In the world of algorithms: Sort Inserts
From the author
This article discusses one of the array sorting algorithms. It is intended for beginners or for those who for some reason are not familiar with this algorithm. Corrections and corrections are welcome :)
Theory
Insertion Sort is a simple sorting algorithm. Its essence lies in the fact that, at each step of the algorithm, we take one of the elements of the array, find the position to insert and insert. It should be noted that the array of the 1st element is considered sorted.
The verbal description of the algorithm sounds quite difficult, but in fact it is the easiest to implement sorting. Each of us, regardless of the type of activity, used a sorting algorithm, just did not realize it :) For example, when sorted bills in a wallet - we take 100 rubles and we look - there are 10, 50 and 500 ruble bills. That's just between 50 and 500 and insert our hundred :) Or give an example of all the books - the game in the card "Fool". When we draw a card from the deck, we look at our cards arranged in ascending order and, depending on the dignity of the drawn card, we place the card in the appropriate place. For greater clarity, I will cite the animation from Wikipedia.
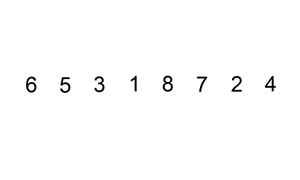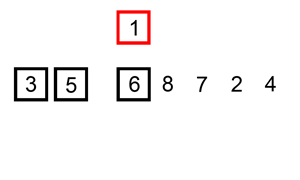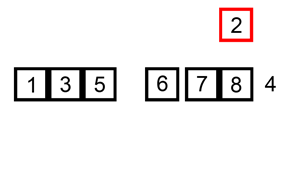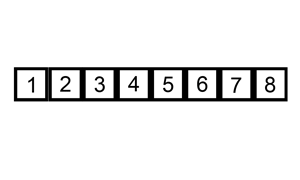
Implementation
Before proceeding with the implementation, we will determine the format of the input data - for example, this will be an array of integer (int) values. The numbering of the elements of the array begins with 0 and ends with n-1. The algorithm itself is implemented in C ++. So let's start ...
The main loop of the algorithm does not start from the 0th element but from the 1st, because the element before the 1st element will be our sorted sequence (remember that the array consisting of one element is sorted) and already relative to this element number 0 we will insert other. Actually code:
')
The implementation of sorting is very simple, only 3 lines. The swap function swaps the elements x [j-1] and x [j]. The nested loop looks for a place to insert. I recommend to remember this algorithm, in order to write a sorting if necessary, not to disgrace by sorting with a bubble :)
Performance analysis
Sorting inserts has a complexity of n 2 , the number of comparisons is calculated by the formula n * (n-1) / 2. The following code was written for the proof:
The number of permutations for 100 items:
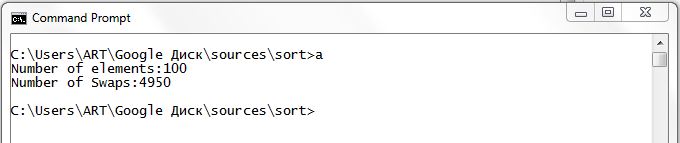
So for n = 100, the number of permutations is 4950, and not 10,000 if we were calculated using the formula n 2 . Keep this in mind when choosing a sorting algorithm.
Efficiency
Sorting by inserts is most effective when the array is already partially sorted and when there are not many elements of the array. If the elements are less than 10, then this algorithm is the best. It’s not in vain that quick sorting (optimization of Bob Sedgwick) uses an insert sorting algorithm as an auxiliary one, but we'll talk about this algorithm later ...
This article discusses one of the array sorting algorithms. It is intended for beginners or for those who for some reason are not familiar with this algorithm. Corrections and corrections are welcome :)
Theory
Insertion Sort is a simple sorting algorithm. Its essence lies in the fact that, at each step of the algorithm, we take one of the elements of the array, find the position to insert and insert. It should be noted that the array of the 1st element is considered sorted.
The verbal description of the algorithm sounds quite difficult, but in fact it is the easiest to implement sorting. Each of us, regardless of the type of activity, used a sorting algorithm, just did not realize it :) For example, when sorted bills in a wallet - we take 100 rubles and we look - there are 10, 50 and 500 ruble bills. That's just between 50 and 500 and insert our hundred :) Or give an example of all the books - the game in the card "Fool". When we draw a card from the deck, we look at our cards arranged in ascending order and, depending on the dignity of the drawn card, we place the card in the appropriate place. For greater clarity, I will cite the animation from Wikipedia.
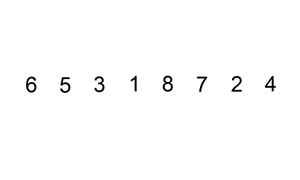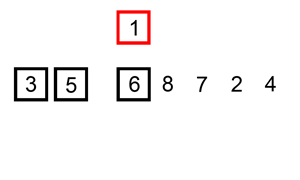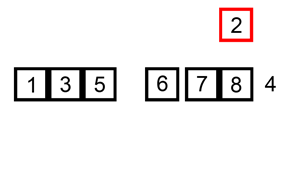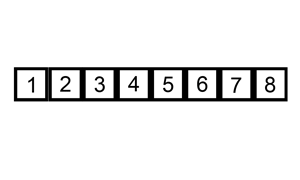
Implementation
Before proceeding with the implementation, we will determine the format of the input data - for example, this will be an array of integer (int) values. The numbering of the elements of the array begins with 0 and ends with n-1. The algorithm itself is implemented in C ++. So let's start ...
The main loop of the algorithm does not start from the 0th element but from the 1st, because the element before the 1st element will be our sorted sequence (remember that the array consisting of one element is sorted) and already relative to this element number 0 we will insert other. Actually code:
')
for(int i=1;i<n;i++) for(int j=i;j>0 && x[j-1]>x[j];j--) // j>0 j-1 > j, x- int swap(x[j-1],x[j]); // j j-1 The implementation of sorting is very simple, only 3 lines. The swap function swaps the elements x [j-1] and x [j]. The nested loop looks for a place to insert. I recommend to remember this algorithm, in order to write a sorting if necessary, not to disgrace by sorting with a bubble :)
Performance analysis
Sorting inserts has a complexity of n 2 , the number of comparisons is calculated by the formula n * (n-1) / 2. The following code was written for the proof:
void Sort(int* arr,int n){ int counter=0; for(int i=1;i<n;i++){ for(int j=i; j>0 && arr[j-1]>arr[j];j--){ counter++; int tmp=arr[j-1]; arr[j-1]=arr[j]; arr[j]=tmp; } } cout<<counter<<endl; } The number of permutations for 100 items:

So for n = 100, the number of permutations is 4950, and not 10,000 if we were calculated using the formula n 2 . Keep this in mind when choosing a sorting algorithm.
Efficiency
Sorting by inserts is most effective when the array is already partially sorted and when there are not many elements of the array. If the elements are less than 10, then this algorithm is the best. It’s not in vain that quick sorting (optimization of Bob Sedgwick) uses an insert sorting algorithm as an auxiliary one, but we'll talk about this algorithm later ...
Source: https://habr.com/ru/post/181271/
All Articles