Geekly Articles each Day
📜 ⬆️ ⬇️

The algorithm of the game "sea battle": the shelling of the enemy

Good day, dear! It so happened that the question of programming more or less adequate AI for the game "sea battle" I was puzzled somewhere in late 2004. Perhaps I, without having proper guidance at hand, invented the bicycle then, but later, I came across stunningly honest algorithms: to shoot at random, from time to time spying the layout of ships at the player, to level the balance. Later I improved the algorithm several times. According to the latest articles on Habré, you can judge that the topic is relevant, besides - I have something to add to what has been written by other users.
So, the purpose of my note: the implementation of the optimal one of the strategies of attack on the opponent's ships , and not only the first hit, but also the subsequent "tracking to the bottom." I note that the ships in my implementation are almost (about this below) of arbitrary shape.

Introduction


I allow myself to reduce the introductory part - for the integrity of the picture I recommend to refer to the preceding articles:


Immediately I apologize for some jargon caused by the desire not to complicate the narration with cumbersome turns, such as “the cage belonging to the ship’s hull” instead of “deck” (in my childhood we called ships “four-deck”, “single-deck”, etc.) I know why).
I note that the ships may have any shape, but each cell belonging to the hull ("deck") must be connected with the rest horizontally and / or verticals and / or diagonals.
Coordinate grid (in the figures with visualization of the playing field): from left to right - numbers, from top to bottom - letters.

Note


The article does not consider code-level optimization, and the algorithms are given in the maximum detailed (detailed) form.
In addition to the explanatory drawings, the article contains screenshots of my programs / games.
')

Modes


Two strategies (two modes) can clearly be distinguished in a combat strategy.


Most people, "wounding" the enemy ship, is trying to sink it. This is logical, since the sinking will make senseless for firing an additional (buffer) zone around the sunken ship, increasing the amount of information about the enemy field and reducing the likelihood of firing. In addition, it is guaranteed that the next point occupied by the ship will be calculated, the worst, in 4 (with diagonal ships in 8) moves, while an attempt to build a new ship may be much less productive.
Thus, the AI ​​starts work in the "Intelligence" mode, in case of non-critical damage ("wounded") the enemy vessel goes into the "Finishing" mode. In the second mode, the AI ​​operates until the ship is destroyed, after which the first mode is selected again.
When optimizing the algorithm for a “classic” squadron (with ships without bends), it may be convenient to select the third mode (see below). The first and second modes are distinguished by the peculiarities of the formation of a probability matrix (about this below), and the logic of the regime change.

Intelligence service


In order to achieve the level of abstraction that allows you to attack a squadron formed from an arbitrary number of vessels of arbitrary shape (however, according to the rules, this information about the opponent is known in advance), we introduce the concept of the probability of a piece of an offensive ship in this cell of the playing field (“decks "). The criterion for selecting the attack point will be a value proportional to the probability mentioned above, namely: the normalized number of decks that can get into this cell, if each of the enemy ships (of those that are afloat) try to place on the field in all possible ways.
Let me explain: we take the matrix (hereinafter - the "P-matrix"), the size corresponding to the size of the enemy field. Fill it with zeros. We take the first available (that is, not yet sunk) enemy ship from the list of the opponent ships and try to place it (in accordance with the rules and based on the information obtained during the shelling) in A1 coordinates. If we were able to place it, then we increment all elements in the P-matrix (corresponding to the cells of the playing field) covered by the ship's hull. Repeat the procedure for all coordinates. Then we turn the ship 90 degrees and repeat the passage for all coordinates again. The same is repeated for 180 and 270 degrees.
As a result, we will fill the P-matrix with values ​​that, for convenience, we normalize to a maximum. The obtained characteristic takes a single value at the most probable points where ships are located and zero at impossible. For example, on the non-shot map, the center points (for the classic squadron) have the maximum value.
It is worth deciding on the term " probability " in order to avoid its erroneous interpretation. This algorithm assumes a uniform arrangement of ships across the field. Attempts to push ships along the edges of the field should be detected separately. For example, you can enter a weight matrix, which will somehow be formed in the course of training (previous games with this opponent): if the enemy never put the ship in the center of the field before, then the corresponding cells of the weight matrix will have a minimum coefficient. In any case: this is not chess - there is always unknown information that, with luck, can give an advantage to the “defender”.
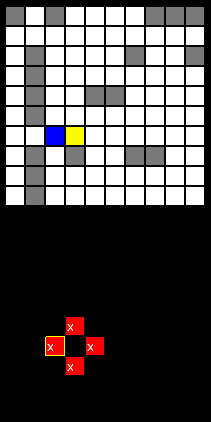
The figure on the left shows the visualization of the P-matrix during the first move of the AI ​​in a game with a classic squadron. Color [RGB (0; 0; 0); RGB (255; 0; 0)] shows the value of the cell. The white cross marks the maximum values. As it is easy to notice, there are usually several maxima. To diversify the game and eliminate the potential possibility to predict the attack point chosen by the AI ​​(and arrange the ships accordingly), we will choose an arbitrary point from the maxima (in the figure it has a yellow frame).
Answers of the opponent "by" or "killed" leave the AI ​​mode unchanged (in the second case, a number of actions are necessary). Answers are stored in a special matrix that accumulates knowledge about the alignment of enemy forces. It is " on this matrix " that attempts are made to locate ships when calculating the P-matrix.
When using only the classic squadron, it is possible to optimize the calculation of the matrix (see below).

Finishing moves


After the answer “wounded” is received from the opponent, the AI ​​switches to the second mode of operation.
In this mode, when calculating the P-matrix, the number of “decks” of the inspected ship must be greater than the number of cells “wounded”. The ship increments the values ​​of the elements of the P-matrix only if its placement covers all cells marked as “wounded”. After going through all the ships there is an additional emphasis on the cells "wounded". Since it is pointless to shoot at such cells (but, unlike “by” cells, they are part of the ship, and therefore have a non-zero value in the P-matrix), the values ​​of the corresponding elements of the P-matrix are reset. The cells that are not adjacent to any of the cells "wounded" are also reset. The latter circumstance is due to the fact that under certain circumstances, reinforced by the exotic shape of ships of a non- classical squadron, you can choose a maximum in the P-matrix that corresponds to the other ship (which is possible only if the attacked cell is separated from the "wounded"). This situation will cause the AI ​​to try to pick up a ship that satisfies both cells, which sooner or later will end in failure. This in turn will lead to the fact that all elements of the P-matrix will take zero values, and, therefore, already fired points will become adequate attack options. Therefore, the attack of nearby points is reasonable.
The figure on the left shows two matrices (more precisely, the visualization of their values). Upper - with gray ships located on a white field. On the previous move, the AI ​​made a successful attack on G4 (the fact that the very first move was a success - a coincidence), the "wounded" cell is marked in yellow. Below is the P-matrix. Considering the geometry of the current set of ships, the AI ​​had 4 equally probable attack variants (marked with a cross-box), from which he chose 3 (a cell with a yellow frame). The move ended with a slip (blue cell in the upper matrix).
When recruiting ships with exotic geometry, the matrices may look much more mysterious . Although I used to play with the classic squadron, I do not see anything reprehensible in the use of ships of almost arbitrary shape. Such models can simulate, for example, high-speed catamaran , RV FLIP , heavy aircraft-carrying cruiser , "concrete battleship" . Not to mention the fact that fixed (according to the logic of the game) objects can also be interpreted as being of limited mobility (or stationary) strategic objects on land during a global war. From the standpoint of the gameplay, in my opinion, this complication only adds to the excitement of the game.
The picture on the right shows the situation: after several successful volleys, the AI ​​chooses the wrong direction and misses the E13. Please note that there were 10 options for a move that made sense, of which 2 are the most likely.
The “finishing” mode switches to “intelligence” only after the opponent’s answer “killed”. As in the first mode, the information obtained during the shelling is taken into account when forming the P-matrix on the next turn.

Classic


Using the classic squadron, that is, "one-dimensional" ships, allows you to specify the approach, reducing the number of operations. On the one hand, the algorithms described below are less flexible and save crumbs of performance (considering the current level of technology, and a large, due to the genre, time per move), but on the other hand, these algorithms are closer to the human perception of the game, which can facilitate understanding of the process functioning of AI.
I note that the specificity of the geometry of classic ships (namely, one-dimensionality) makes the probability to place the hull, rotated 180 degrees (depending on the point of rotation - with the corresponding coordinate correction) equal to the probability of placing the hull with zero angle of rotation. In other words, it is impossible to determine for all ships: it is located from top to bottom or bottom to top, from left to right or from right to left (see the figure on the left: 4 angles of rotation for the gray hull and 2 for the classic brown). This circumstance allows us to reduce the number of calculations, leaving only the placement test for all ships at an angle of 0 and 90 degrees.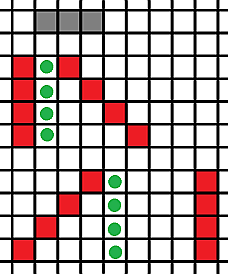
The one-dimensionality makes it possible to determine the number of “decks” entering the cell, relying only on the length of the ship and the distance to the obstacles. In the figure on the right: obstacle cells (for example, buffer zones of other ships) are marked in red, the green circle is the cell for which the characteristic is calculated. An attempt is made to place a ship three cells long. It is easy to estimate that the results (from top to bottom) will be as follows: 0, 0, 1, 1. Obviously, in the first two cases, the distance between the obstacles is fundamentally not enough for the body of the required length. In the fourth case, it becomes clear that to increase the number of possible positions of the ship, you can only pushing the opposite border.
We begin to move the obstacle on the left, and we get the characteristics: 1, 2, 3, 3. From the results it can be seen that the characteristic is limited from above by the length of the ship.
Summarizing:

Based on the foregoing, the code of the function that calculates the characteristic is:
inline unsigned minimum(unsigned A,unsigned B){ return A<B?A:B; } unsigned Bf(unsigned A,unsigned B,unsigned K){ if(A+B+1<K) return 0; if(A+B+1==K) return 1; return minimum(minimum(A,B)+1,K); }

If there are several ships of the same length in an enemy squadron, then in order to take into account their total effect on the cell, it is enough to count Bf once and multiply the result by the number of units of equipment. After going through all the unique lengths of the enemy ships (for the classic - 4 options) and taking into account the number of ships with such a hull length afloat, we get a certain characteristic Gf . This characteristic describes the number of "decks" that fall into a cell at a fixed orientation (but not coordinates) of all ships (for example, for the figure above - horizontal). The summary characteristic of G2df is the sum of Gf for horizontal and vertical orientation. The matrix of G2df values ​​for all cells of the playing field is analogous to the P-matrix, discussed above. Based on the maximums of the matrix, choose the point of attack. If successful, go to the finishing mode, where we select the cell that corresponds to the most free (but within the maximum hull length among the undestroyed enemy ships) direction. If several directions are equally probable, we choose randomly. Having chosen the direction of the attack, we continue to fire to one of the outcomes:


Conclusion


So, now you know how to fire at the enemy, and how best to place the ships (see links at the beginning of the article).
I myself would like to know the thoughts of the community about the non-optimal (uniform) placement of ships: even in the classic version, a deadlock is possible if you do not move the already exposed ships. For ships of arbitrary shape, you can probably justify the criterion for the minimum size of the field for placement.
Thanks to all who read the article to the end. I will try to answer your questions.
Request: instructions on errors and other suggestions for editing, write in a personal, so as not to dilute the discussion.

Criticism


Thanks for the interesting and constructive comments!

mayorovp clarifies that the considered algorithm works optimally only in a certain approximation. In fact, consider the proposed situation:
there are five cells in a line and two 1x2 ships left in the field, then the optimal algorithm will destroy them in 4 shots without a slip. Your algorithm will determine that the "probability" of finding the ship in the center is maximum, and may try to shoot there (in one case out of three).

Really:

Unlike the optimal tactic obvious to a man, the AI ​​will, with a 33% probability, take an a priori wrong decision, attacking A3 on the Nth move. On the (N + 1) th move (if successful on the Nth), an erroneous attack can be realized with a probability of 50% (in the picture, an attack on A3 on the second slide).
As mayorovp notes,
The optimal algorithm should
1) when calculating the probability to place not one ship on the field, but the entire enemy squadron, taking into account the limitations on the neighborhood;
There is also a weakness of adaptation to the uneven distribution of ships on the playing field during the training:
2) take into account that the enemy can intentionally place his squadron in the least likely position (at the edges, for example), and take retaliatory actions already in the first game, instead of training for a specific opponent.


MichaelBorisov cites a link to his study "Boat for the game of" sea battle ": history, theory, practice . "
Unfortunately, my “all-encompassing” approach encountered computational difficulties, that even on modern computers it is impossible to calculate all the combinations, but one can only look for some approximation using the Monte-Carlo method, but this also turned out to be difficult in real time.

zorge_van_daar raises an interesting question: is it possible, instead of finishing, to switch to the search for new ships (taking into account the information obtained after the attack), since it is possible to detect all the enemy equipment and is the main goal of the game, and you can destroy it later.

For the well-grounded advice of limon_spb and other users, removed the overly ambitious "optimal" characteristic. Since such a statement requires objective evidence, which is not given in the article, and, by virtue of the foregoing, cannot be given.

Source: https://habr.com/ru/post/181151/

More articles:


All Articles