Entropy and WinRAR - detailed answer

A few days ago, an article on Entropy and WinRAR was published on Habré. Some inaccuracies are noticed in it, for which I want to give a detailed answer.

I'll start with a simple one - the picture “the degree of compression of various data.” Here she is:


')
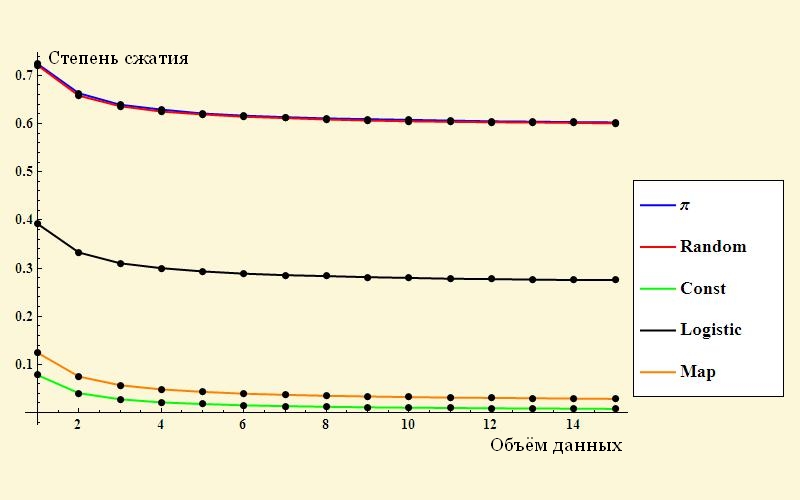
Surprisingly, a random sequence of numbers is compressed somewhere up to 60% of the original volume. I remember exactly in my youth I tried to compile compressed video and pictures in jpg. The archives were almost the same size as the original, and sometimes a couple percent more! Unfortunately, the author of the article did not describe in detail how exactly he got his result. The degree of compression of his sequence of random numbers is suspiciously similar to the ratio 10/16 = 0.625.

I tried to reproduce the experiment on my own. I generated a file with random characters, and then compressed it with the winRar mentioned in the header. The result is:

file size	Archive size
1,000,000 bytes	1 002 674 bytes
100,000 bytes	100 414 bytes
10,000 bytes	10,119 bytes

As you can see, with a randomly generated sequence of data, the size of the archive is larger than the size of the source file, which is to be expected.

Funny observation: to generate a file, I wrote a small program in java. The actual generation was done by the team.

dataOutputStream.writeChar((int) (Math.random() * 65536));


Let me explain: Java supports Unicode, so the type char takes 2 bytes. That is, is a number from 0 to 65535. Math.random () gives a number from 0 to 1, a random symbol is obtained by multiplying by a coefficient, which can be any available symbol with equal probability.

A funny observation: at first the program was written with an error, instead of 65536 it was 16536. As a result, the file with random characters was compressed to 95% of the original. In principle, this is also the expected result. Check it by the formula.
I will use the formula given in the original article:



We assume that the characters in our file appear independently. At each position, 16536 different symbols are possible, the probability of each outcome is the same and equal. So the amount is calculated as follows:

H = - (1/16536 * log (1/16536)) * 16536 = 14

Hereinafter, the logarithm is taken over the base 2.

However, the archiver allows you to use all 65,536 values ​​for every 2 bytes. The entropy to the archive symbol is

H = - (1/65536 * log (1/65536)) * 65536 = 16

The entropy ratio of 14/16 = 0.875 - a little less than 0.95, obtained as a result of archiving is also a completely natural result.

I suspect that the author of the original article generated numbers in the decimal system, and after compression, these numbers were encoded in hexadecimal format. This allows the archiver to compress the data in a relation that aspires to 10/16.

The second point that I would like to comment on. As you have noticed, the entropy formula contains such a quantity as the probability of obtaining one or another value. It seems to me that this probability is not so obvious, and it deserves a separate large article. I just considered the simplest case, when all the characters in our message are independent of each other, each value appears randomly. In this case, everything is simple: we can talk about the likelihood of each value. If the file is generated, we can set this probability. If the file comes from the outside - we can measure the frequency of occurrence of each character and, with a sufficiently long message, it will tend to probability.

However, the reality is not so simple. Take for example the text - coherent sentences in human language. If we consider it as a stream of independent letters, you can see that the letters have different frequencies, they can be compared with the probability and achieve a certain degree of compression. However, in natural language, some pairs and triples of letters are practically not found - the work of, for example, the well-known PuntoSwitcher is based on this. Those. the likelihood of the current letter depends on what came before it. This helps reduce uncertainty and achieve an even greater degree of compression. You can move on: the text consists of words. The vocabulary of the author of the text certainly does not exceed 4096 words, which will give 12 bits per word. Here you need to add 3 bits for about 8 cases or conjugations - a total of 15 bits. The average word of the Russian language consists of 6 letters - it is 48 bits in ASCII or 96 bits in Unicode. By the way, some words are more common than others, the same with cases - it means that the average number of bits per word will be even less (rare words can be encoded with a longer sequence of bits, and frequent words with a shorter one).

But that is not all. We can move to the level of sentences - this will make it possible to predict which word will most likely follow the preceding ones, and thus reduce the entropy of the message even more.

One should not think that all these difficulties are characteristic only of natural texts. In the article I comment on, the author squeezed the sequence of characters of Pi. There are no random characters in this sequence, and a highly intelligent archiver could recognize this. In this case, the archive of any number of characters of Pi would represent, for example, the following entry:

[formula for calculating characters of pi] [number of characters]

As can be seen, the length of this record will grow logarithmically with respect to the length of the original sequence (for encoding 999 characters, you need to write the formula + 3 decimal digits, and for encoding 9999 symbols - 1 decimal digit more, an additional symbol will be needed to write "9999"). Divide the length of the "archive" by the length of the original sequence to obtain the compression ratio and estimate the entropy per symbol. This ratio will tend to zero with an increase in the length of the original sequence, as it should be for non-random source data. Yes, unpacking such an archive will require some computational resources, but then even ordinary archives are not unpacked by themselves.

All this does not disprove the formula for calculating the entropy, but simply illustrates what tricks can be hidden behind the letter p, denoting probability.