Entropy and WinRAR

The concept of entropy is used in almost all areas of science and technology,
from designing boiler rooms to models of human consciousness.
The basic definitions of both thermodynamics and dynamic systems and methods of computation are not difficult to understand. But the farther into the forest - the more firewood. For example, I recently found out (thanks to R. Penrose, “The Path to Reality”, pp. 592-593) that not only solar energy is important for life on Earth, but its low entropy.

If we confine ourselves to simple dynamical systems or one-dimensional data arrays (which can be obtained as the “trace” of the system’s motion), then at least three definitions of entropy can be counted as measures of randomness.
The deepest and most complete of them (Kolmogorov-Sinai) can be clearly studied,
using file archiver programs.

Introduction

Referring to the informational entropy, they often simply give Shannon's “magic” formula:

where N is the number of possible realizations, b is the units of measurement (2 are bits, 3 are trits, ..), p _i are the probabilities of realizations.
Of course, everything is not so simple (but interesting!). For the first (as well as the second, and even the third) acquaintance, I recommend a book that is not outdated by A. Yagl and I. Yagl, Probability and Information, 1973.
In response to the "childish" question: " What does the number obtained by the formula mean?"
Such a graphic illustration will do.

Suppose there are N = 16 cells, one of which is marked with a cross:
')
[] [] [] [] [] [] [] [] [] [] [] [x] [] [] [] []]

The choice is random; the probability that the i-th cell is marked is equal to p _i = 1/16
Shannon's entropy is

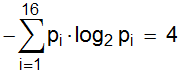
Now imagine a game; one player draws cells, puts a cross and tells the second only
cell count. The second is to find out which one is marked and asks questions;
but the first one will answer only “Yes” or “No”.
How many (minimum!) Questions need to be asked to find out where the cross is?
The answer is " 4 ". In all such games, the minimum number of questions will be equal to the information entropy.
It does not matter what questions to ask. An example of the right strategy is
divide the cells in half (if N is odd, then with an excess / deficit of 1 cell) and ask:
“Cross in the first half?” Having learned that in such and such, we also divide it in half, etc.

Another kind of “naive”, but a deep question: why is there a logarithm in the Shannon formula?
And what exactly is a logarithmic function? Inverse exponential ... And what is exponential?
In fact, rigorous definitions are given in the course of mathematical analysis, but they are not complicated at all.
It often happens that increasing the "input" at times, we get the "output" only by a few more units.
Augustin Cauchy proved that the equation

f (x · y) = f (x) + f (y) x, y> 0

has only one continuous solution ; this is a logarithmic function.
Imagine now that we are conducting two independent tests; the number of outcomes they have is n and m, they are all equally probable (for example, we throw both the dice and the coin at the same time; n = 6, m = 2)
Obviously, the number of outcomes of double experience is equal to the product n · m.
The uncertainties of the experiences add up; and entropy, as a measure of this uncertainty, should
satisfy the condition h (m · n) = h (m) + h (n), i.e. be logarithmic.

Entropy of Kolmogorov-Sinai

The strict definition of this fundamental concept is rather difficult to understand.
We will approach it gradually;
our "phase space" will be one-dimensional arrays of natural numbers.
For example, the decimal digits of the number "Pi": {3, 1, 4, 1, 5, 9, 2, 6, ...}
In fact, any data can be brought into this form (with losses, of course).
It is enough to split the entire range of values ​​into N intervals and, if it hits the k-th interval, record the number k (as with the sound sampling).
How random, stochastic is this or that sequence?
Informational entropy, of course, is a good candidate for the “chaos meter”.
It is not difficult to prove that it is maximal when all probabilities of the appearance of different numbers are equal.

But then the difficulties begin, which I mentioned in a previous post.
For example, the array ... 010101010101010101 ... has the maximum entropy, being the least random sequence of 0 and 1.
If the data is not originally digital (sound, pictures), then you can convert them into numbers from 0 to N in different ways. And probabilities in a numerical array can be measured not only for individual elements, but also for pairs, triples, odd in order, etc.
Well, since there are many options, we use them all!
We will display the "experimental" array in various ways - in different number systems, breaking into pairs and triples, etc. Obviously, its size L and Shannon's entropy H will depend on the mapping method.
For example, considering it as a solid, indivisible object, we get L = 1, H = 0.
Given that H grows with increasing L, we introduce the value



This is the (somewhat simplified) definition of Kolmogorov-Sinai entropy ( strict here). In a theoretical sense, it is perfect.
But it is very difficult to technically find the top edge over all partitions. In addition, for clarity, it will be necessary to arrange all the results in an orderly manner, and this is a separate serious task.
Fortunately, there is an approach that almost does not weaken the strictness of the theory, but is much more visual and
practical.

Archiving and entropy

About methods and algorithms of information compression on Habré were told more than once
habrahabr.ru/post/142242
habrahabr.ru/post/132683
not to mention the original sources.
At one time, the possibility of compressing up to 50% with full recovery made a shocking impression on me.
He was no less surprised when he found out that the relationship between the degree of data compression and their Kolmogorov-Sinai entropy was strictly proved . Intuitively, this is understandable - the more ordered the data, the more possibilities for compression encoding.
However, rigorous mathematical considerations do not always confirm “common sense”;
and although the articles on this topic are quite intricate (and the main one is also paid), we will believe theorists that everything is legal and proceed to the experiments.

Create data of 4 types:

• decimal digits of pi (π)
• GPSN Wolfram Mathematica (Random)
• the brightest and simplest example of deterministic chaos - logistic mapping (Logistic)
• array of one "1" (Const)
• some kind of glitzy formula that at first glance generates random numbers (Map)

Of course, we can calculate entropies using the Shannon formula (embedded in Mathematica as Entropy []).
However, as mentioned above, the result will strongly depend on the number system, the form of data presentation, etc.
Here, for example, is a logistic entropy graph for an ever-increasing amount of data:



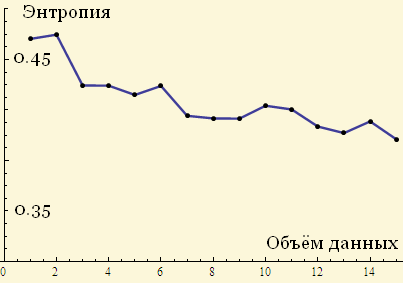
It is not very clear whether the entropy tends to a certain value as the size of the array increases.
And now let's try to measure entropy using compression. For each example, we will make arrays of different sizes and construct graphs of the “size after compression / size before compression” relationship depending on the array length (to be honest, I used Mathematica zip archiver, which was not included in the WinRAR header).



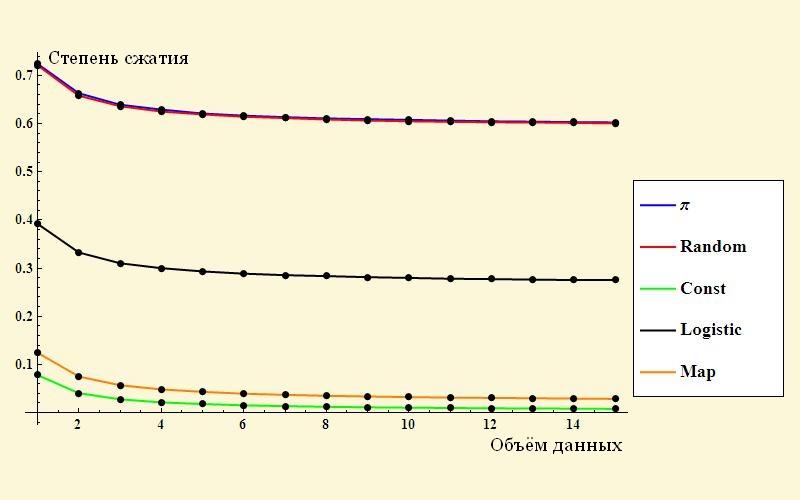
These are the right, “wine” pictures! It is clearly seen how the compression ratio goes to the limit value, which characterizes the measure of randomness of the original data.
Let me remind you that the less ordered the data, the harder it is to encode it.
The largest residual volume is in the digits of Pi and random numbers (almost merged blue and red
graphics).

An example of the development of ideas.

Instead of “boring” numbers, we take meaningful literary texts. The degree of their stochasticity and methods of compression is a very broad topic (see for example )
Here we just make sure that measurements with the help of archivers also make sense.
Approximately equal fragments of Russian fairy tales, spiritual conversations of Jidda Krishnamurti and LI speeches were taken as examples. Brezhnev.



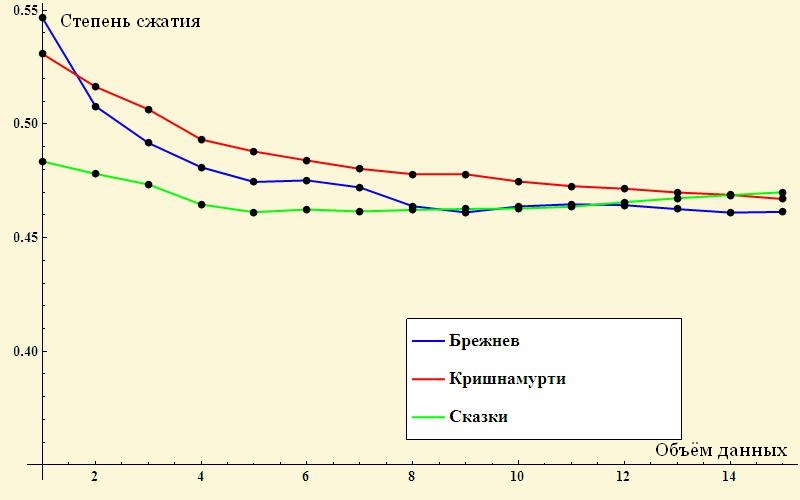
Interestingly, for small passages, the compression ratio (that is, the ordering) of the texts is noticeably different, while Brezhnev is the leader (!) But for large arrays, the entropy of the texts is about the same. What this means and whether it always means is unknown.