Game Life and Fourier Transform
Many have heard of the great and terrible fast Fourier transform (FFT / FFT - fast fourier transform) - but how it can be used to solve practical problems with the exception of JPEG / MPEG compression and sound decomposition in frequencies (equalizers, etc.) - it is often unclear .I recently stumbled upon an interesting implementation of Conway’s Life game using the fast Fourier transform — and I hope it helps you understand the applicability of this algorithm in quite unexpected places.
rules
Recall the rules of the classic "Life" - on a field with square cells, a living cell dies if it has more than 3 or less than 2 neighbors, and if an empty cell has exactly 3 neighbors, it is born. Accordingly, for the effective implementation of the algorithm, you need to quickly count the number of neighbors around the cell.')
Algorithms for this there is a whole bunch (including my JS implementation ). But the task has a mathematical solution, which can give a good speed for densely filled fields, and quickly goes into the lead with an increase in the complexity of the rules and the area / amount of summation - for example, in Smoothlife-like ( 1 , 2 ), and 3D versions.
FFT implementation
The idea of the algorithm is as follows:- We form the summation matrix (filter), where 1 are in the cells, the sum of which we need to get (8 units, the remaining zeros). We perform a direct Fourier transform on the matrix (this needs to be done only 1 time).
- Perform a direct Fourier transform on the matrix with the contents of the playing field.
- Multiply each element of the result by the corresponding element of the "summation" matrix from item 1.
- Perform the inverse Fourier transform - and obtain a matrix with the sum of the number of neighbors for each cell we need.
C ++ implementation
//Author: Mark VandeWettering http://brainwagon.org/2012/10/11/crazy-programming-experiment-of-the-evening/ #include <stdio.h> #include <stdlib.h> #include <math.h> #include <complex.h> #include <unistd.h> #include <fftw3.h> #define SIZE (512) #define SHIFT (18) fftw_complex *filter ; fftw_complex *state ; fftw_complex *tmp ; fftw_complex *sum ; int main(int argc, char *argv[]) { fftw_plan fwd, rev, flt ; fftw_complex *ip, *jp ; int x, y, g ; srand48(getpid()) ; filter = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ; state = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ; tmp = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ; sum = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ; flt = fftw_plan_dft_2d(SIZE, SIZE, filter, filter, FFTW_FORWARD, FFTW_ESTIMATE) ; fwd = fftw_plan_dft_2d(SIZE, SIZE, state, tmp, FFTW_FORWARD, FFTW_ESTIMATE) ; rev = fftw_plan_dft_2d(SIZE, SIZE, tmp, sum, FFTW_BACKWARD, FFTW_ESTIMATE) ; /* initialize the state */ for (y=0, ip=state; y<SIZE; y++) { for (x=0; x<SIZE; x++, ip++) { *ip = (fftw_complex) (lrand48() % 2) ; } } /* initialize and compute the filter */ for (y=0, ip=filter; y<SIZE; y++, ip++) { for (x=0; x<SIZE; x++) { *ip = 0. ; } } #define IDX(x, y) (((x + SIZE) % SIZE) + ((y+SIZE) % SIZE) * SIZE) filter[IDX(-1, -1)] = 1. ; filter[IDX( 0, -1)] = 1. ; filter[IDX( 1, -1)] = 1. ; filter[IDX(-1, 0)] = 1. ; filter[IDX( 1, 0)] = 1. ; filter[IDX(-1, 1)] = 1. ; filter[IDX( 0, 1)] = 1. ; filter[IDX( 1, 1)] = 1. ; fftw_execute(flt) ; for (g = 0; g < 1000; g++) { fprintf(stderr, "generation %03d\r", g) ; fftw_execute(fwd) ; /* convolve */ for (y=0, ip=tmp, jp=filter; y<SIZE; y++) { for (x=0; x<SIZE; x++, ip++, jp++) { *ip *= *jp ; } } /* go back to the sums */ fftw_execute(rev) ; for (y=0, ip=state, jp=sum; y<SIZE; y++) { for (x=0; x<SIZE; x++, ip++, jp++) { int s = (int) round(creal(*ip)) ; int t = ((int) round(creal(*jp))) >> SHIFT ; if (s) *ip = (t == 2 || t == 3) ; else *ip = (t == 3) ; } } /* that's it! dump the frame! */ char fname[80] ; sprintf(fname, "frame.%04d.pgm", g) ; FILE *fp = fopen(fname, "wb") ; fprintf(fp, "P5\n%d %d\n%d\n", SIZE, SIZE, 255) ; for (y=0, ip=state; y<SIZE; y++) { for (x=0; x<SIZE; x++, ip++) { int s = ((int) creal(*ip)) ; fputc(255*s, fp) ; } } fclose(fp) ; } fprintf(stderr, "\n") ; return 0 ; } To build the necessary library FFTW . Keys to build in gcc:
gcc life.cpp -lfftw3 -lm -lstdc ++Visual Studio needs changes in working with complex numbers.
Images during the execution of the algorithm:
Initial filter matrix (the origin is the upper left corner, the field is "looped"):
The real part of the filter after the direct FFT:
Source field - 1 glider:
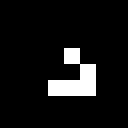
FFT source field, real and imaginary parts:
After multiplying by the filter matrix:
After the inverse FFT, we get the sums:
The result is quite expected:
The "looping" of the field is obtained automatically due to the FFT.
FFT buns
- You can sum any number of elements with any coefficients — and the running time remains fixed , N 2 logN. Those. while for classical life, the usual algorithms on the filled fields are still quite fast, then with an increase in the area / volume of summation, they become slower and the speed of the FFT operation remains fixed.
- FFT - already written, debugged and optimized perfectly - using all the processor features: sse, sse2, avx, altivec and neon.
- You can easily use all processors and video cards by taking ready multiprocessor and CUDA / OpenCL FFT implementations. Again, you do not need to take care of optimizing the FFT. FFTW by the way supports multiprocessor execution (--enable-openmp at build time), the larger the field - the lower the synchronization loss.
- The same approach applies to 3D space.
Compare the speed of work with the "naive" implementation
FFTW is built in single-precision mode (--enable-float, gives a speed increase of about 1.5 times). The processor is a Core2Duo E8600. gcc 4.7.2 -O3Source code of a naive implementation
for (int i=8; i<1000; i++) { delta[i][0] = (lrand48() % 21)-10; delta[i][1] = (lrand48() % 21)-10; } #define NUMDELTA 18 for(int frame=0;frame<10;frame++) { double start = ticks(); for (y=0; y<SIZE; y++) for (x=0; x<SIZE; x++) { int sum=0; for(int i=0;i<NUMDELTA;i++) sum+=array[readpage][(SIZE+y+delta[i][0]) % SIZE][(SIZE+x+delta[i][1]) % SIZE]; if(array[readpage][y][x]) array[1-readpage][y][x] = (sum>3 || sum<2)?0:1;else array[1-readpage][y][x] = (sum==3)?1:0; } readpage = 1-readpage; printf("NaiveDelta: %10.10f\n", ticks()-start); } | Test configuration | At what amount of cells to be summed up, the speed of FFT and naive realization is equal to |
| 1 core, 512x512 | 29 |
| 2 cores, 512x512 | 18 |
| 1 core, 4096x4096 | 88 |
| 2 cores, 4096x4096 | 65 |
Update:
As it turned out, FFTW, when specifying the FFTWESTIMATE flag, uses far from optimal FFT calculation plans. When specifying FFTW_MEASURE, the speed has greatly increased, and the situation looks more joyful (when summing up less than 18 cells, the naive implementation sharply becomes 3 times faster, because everything rests on 18):
| Test configuration | At what amount of cells to be summed up, the speed of FFT and naive realization is equal to |
| 1 core, 512x512 | 18 |
| 2 cores, 512x512 | 18 |
| 1 core, 4096x4096 | 28 |
| 2 cores, 4096x4096 | nineteen |
No matter what - mathematics in programming can sometimes be useful in the most unexpected places.
And may the power of FFT be with you!
Source: https://habr.com/ru/post/180135/
All Articles