The program for drawing a four-dimensional cube
Let's start with an explanation of what four-dimensional space is.
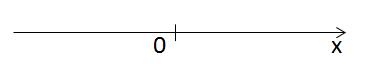
This is a one-dimensional space, that is, simply the axis OX. Any point on it is characterized by one coordinate.
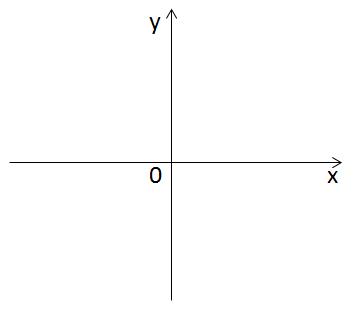
We now draw the OY axis perpendicular to the OX axis. So it turned out two-dimensional space, that is, the plane XOY. Any point on it is characterized by two coordinates - the abscissa and the ordinate.
')
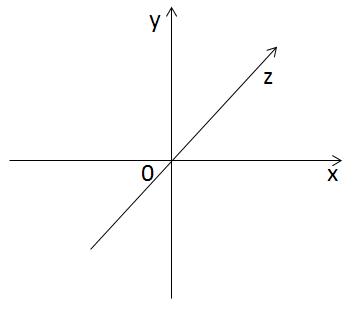
Draw the axis OZ perpendicular to the axes OX and OY. The result is a three-dimensional space in which any point has an abscissa, ordinate, and applicate.
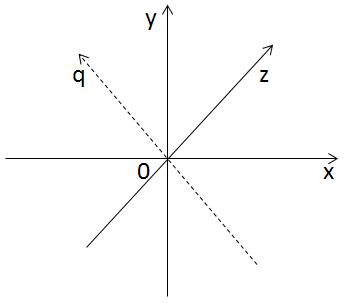
It is logical that the fourth axis, OQ, should be perpendicular to the axes OX, OY and OZ simultaneously. But we cannot precisely construct such an axis, and therefore it remains only to try to imagine it. Each point in the four-dimensional space has four coordinates: x, y, z and q.
Now let's see how the four-dimensional cube appeared.
The picture shows a figure of one-dimensional space - the line.
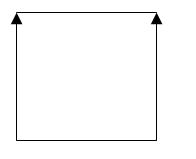
If you make a parallel transfer of this line along the OY axis, and then connect the corresponding ends of the two resulting lines, you will get a square.
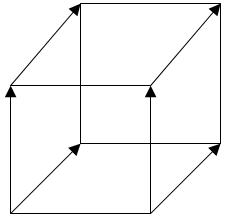
Similarly, if you make a parallel transfer of a square along the OZ axis and connect the corresponding vertices, you will get a cube.
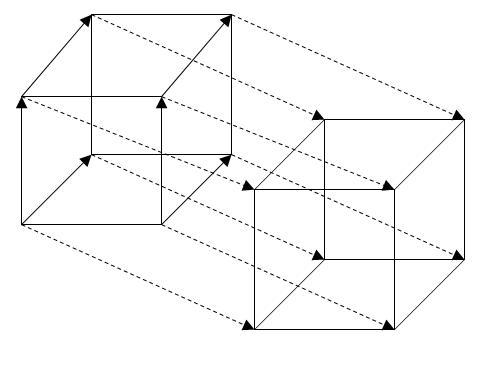
And if you make a parallel transfer of the cube along the OQ axis and connect the vertices of these two cubes, then we get a four-dimensional cube. By the way, it is called a tesseract .
To draw a cube on a plane, you need to project it . It clearly looks like this:
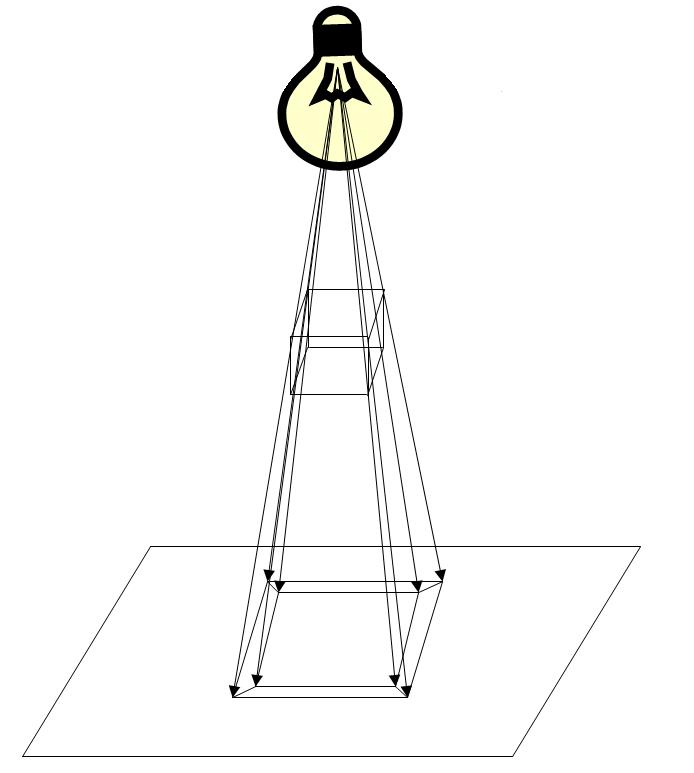
Imagine that a frame model of a cube hangs in the air above the surface, that is, as if made of wire, and a light bulb above it. If you turn on the light bulb, draw a pencil around the shadow of the cube, and then turn off the light bulb, then the projection of the cube will be displayed on the surface.
We turn to a little more complicated. Look again at the drawing with a light bulb: as you can see, all the rays converged at one point. It is called a vanishing point and is used to construct a perspective projection (and sometimes parallel, when all the rays are parallel to each other. The result is not a sensation of volume, but it is lighter, and if the vanishing point is sufficiently far from the projected object, then the difference these two projections are hardly noticeable). To project a given point on a given plane, using the vanishing point, you need to draw a straight line through the vanishing point and this point, and then find the intersection point of the resulting straight line and plane. And in order to project a more complex shape, say, a cube, you need to project each of its vertices, and then connect the corresponding points. It should be noted that the algorithm of the projection of space on a subspace can be generalized for the case of 4D-> 3D, and not just 3D-> 2D.
As I have already said, we cannot imagine for sure exactly what the OQ axis looks like, nor does the tesseract. But we can get a limited idea of it, if we project it on volume, and then draw it on the computer screen!
Now let's talk about the tesseract projection.
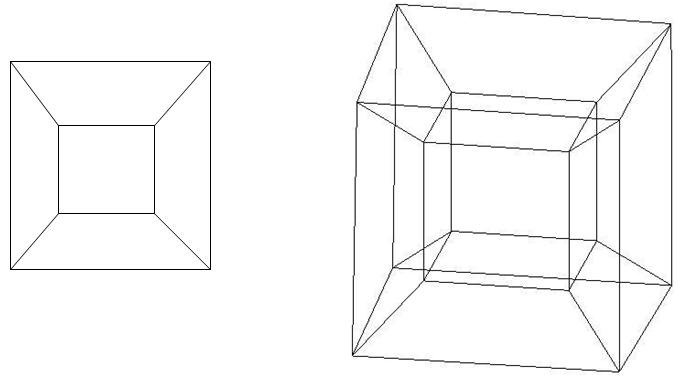
On the left is the projection of the cube onto the plane, and on the right is the tesseract on the volume. They are quite similar: the projection of the cube looks like two squares, small and large, one inside the other, and whose corresponding vertices are connected by lines. A tesseract projection looks like two cubes, small and large, one inside the other, and whose corresponding vertices are connected. But we all saw a cube, and we can confidently say that a small square, a large one, and four trapeziums above, below, to the right and left of a small square are actually squares, and they are equal. And the tesseract is the same. And the big cube, and the small cube, and the six truncated pyramids on the sides of the small cube are all cubes, with what they are equal.
My program can not only draw a tesseract projection onto a volume, but also rotate it. Consider how this is done.
To begin, I'll tell you what rotation is parallel to the plane .
Imagine that a cube rotates around the axis OZ. Then each of its vertices describes a circle around the axis OZ.
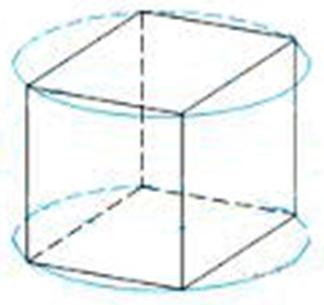
And the circle is a flat figure. And the planes of each of these circles are parallel to each other, and in this case parallel to the XOY plane. That is, we can speak not only about rotation around the OZ axis, but also about rotation parallel to the XOY plane. As we see, for points that rotate parallel to the XOY axis only the abscissa and ordinate change, the applicate remains unchanged And, in fact, we we can talk about rotation around a line only when we are dealing with a three-dimensional space. In two-dimensional everything revolves around a point, in four-dimensional - around a plane, in five-dimensional space we speak about rotation around a volume. And if we can imagine a rotation around a point, then a rotation around a plane and a volume is something unthinkable. And if we talk about rotation parallel to the plane, then in any n-dimensional space a point can rotate parallel to the plane.
Many of you have probably heard of the turn matrix. Multiplying a point on it, we get a point rotated parallel to the plane by an angle phi. For two-dimensional space, it looks like this:
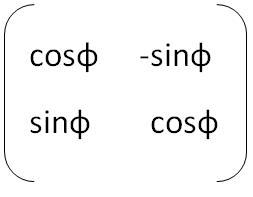
How to multiply: X of a point rotated by phi = cosine of phi * x of the original point minus sine of the angle phi * of the original point;
Yy of a point rotated by phi = sine of phi * x of the original point plus the cosine of phi * of the original point.
Xa` = cosf * Xa - sinf * Ya
Ya` = sinf * Xa + cos * Ya
where Xa and Ya are the abscissa and ordinate of the point to be rotated, Xa` and Ya` are the abscissa and ordinate of the already rotated point
For three-dimensional space, this matrix is summarized as follows:

Rotation is parallel to the XOY plane. As you can see, the Z coordinate does not change, only X and Y change.
Xa` = cosf * Xa - sinf * Ya + Za * 0
Ya` = Sinf * Xa + cosf * Ya + Za * 0
Za` = Xa * 0 + Ya * 0 + Za * 1 (in fact, Za` = Za)

Rotation is parallel to the XOZ plane. Nothing new,
Xa` = cosf * Xa + Ya * 0 - sinf * Za
Ya` = Xa * 0 + Ya * 1 + Za * 0 (in fact, Ya` = Ya)
Za` = sinf * Xa + Ya * 0 + cosf * Za

And the third matrix.
Xa` = Xa * 1 + Ya * 0 + Za * 0 (in fact, Xa` = Xa)
Ya` = Xa * 0 + cosf * Ya - sinf * Za
Za` = Xa * 0 + sinf * Ya + cosf * Za
And for the fourth dimension, they look like this:

I think you have already understood what to multiply, because I will not paint once again. But I note that it does the same thing as the matrix for turning parallel to a plane in three-dimensional space! Both this and this change only the ordinate and applicate, and do not touch the other coordinates, so it can be used in the three-dimensional case, simply ignoring the fourth coordinate.
But the projection formula is not so simple. No matter how I read the forums, none of the projection methods came up to me. Parallel did not suit me, since the projection will not look voluminous. In some projection formulas, to find the point, you need to solve a system of equations (but I don’t know how to teach a computer to solve them), I simply didn’t understand others ... In general, I decided to think of my own way. Consider for this the projection 2D-> 1D.
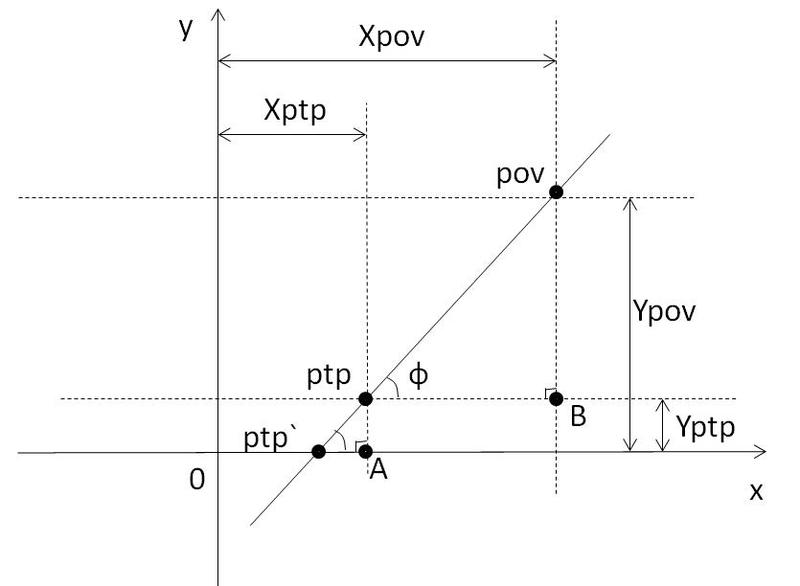
pov means “Point of view” (ptp) means “Point to project” (the point to be projected), and ptp` is the desired point on the OX axis.
The angles povptpB and ptpptp`A are equal as appropriate (the dotted line is parallel to the axis OX, the straight line povptp is the secant).
The x point of the ptp` is equal to the x of the ptp point minus the length of the segment ptp`A. This segment can be found from the triangle ptpptp`A: ptp`A = ptpA / tangent of the angle ptpptp`A. We can find this tangent from the triangle povptpB: the tangent of the angle ptpptp`A = (Ypov-Yptp) (Xpov-Xptp).
Answer: Xptp` = Xptp-Yptp / tangent of ptpptp`A angle.
I did not elaborate on this algorithm here, since there are a lot of special cases where the formula changes somewhat. To whom it is interesting - look in the source code of the program, everything is painted in the comments.
In order to project a point of three-dimensional space on a plane, simply consider two planes - XOZ and YOZ, and for each of them we will solve this problem. In the case of four-dimensional space, it is necessary to consider already three planes: XOQ, YOQ and ZOQ.
And finally, about the program. It works like this: initialize sixteen tesseract vertices -> depending on the commands entered by the user, rotate it -> project to volume -> depending on the commands entered by the user, rotate its projection -> project to the plane -> draw.
Projections and turns I wrote myself. They work according to the formulas that I just described. The OpenGL library draws lines, as well as mixing colors. And the coordinates of the tesseract vertices are calculated as follows:
The coordinates of the vertices of the line centered at the origin and the length of 2 - (1) and (-1);
- "-" - squares - "-" - and an edge of length 2:
(1; 1), (-1; 1), (1; -1) and (-1; -1);
- "-" - cube - "-" -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1 ; -1), (1; -1; -1), (-1; -1; -1);
As you can see, the square is one line above the OY axis and one line below the OY axis; a cube is one square in front of the XOY plane, and one behind it; Tesseract is one cube on the other side of the XOYZ volume, and one on this. But it is much easier to perceive this alternation of units and minus ones if they are written in a column
one; one; one
-one; one; one
one; -one; one
-one; -one; one
one; one; -one
-one; one; -one
one; -one; -one
-one; -one; -one
In the first column, one and minus one alternate. In the second column, there are two plus points first, then two minuses. In the third - four plus units, and then four minus one. These were the tops of the cube. Tesseracts have twice as many of them, and therefore it was necessary to write a cycle to declare them, otherwise it is very easy to get confused.
My program can also draw anaglyph. Happy owners of 3D glasses can watch a stereoscopic image. There is nothing tricky in drawing a picture, just two projections are drawn on the plane, for the right and left eyes. But the program becomes much more visual and interesting, and most importantly - it gives a better idea of the four-dimensional world.
Less significant functions are the highlighting of one of the faces in red, so that you can better see the turns, as well as minor conveniences — adjusting the coordinates of the eye points, increasing and decreasing the speed of turning.
Archive with the program, source code and instructions for use: www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2% D0% B5% D1% 81% D1% 81% D0% B5% D1% 80% D0% B0% D0% BA% D1% 82.rar (you need to download and install the program Dropbox: www.dropbox.com )
Source: docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit
This is a one-dimensional space, that is, simply the axis OX. Any point on it is characterized by one coordinate.

We now draw the OY axis perpendicular to the OX axis. So it turned out two-dimensional space, that is, the plane XOY. Any point on it is characterized by two coordinates - the abscissa and the ordinate.
')

Draw the axis OZ perpendicular to the axes OX and OY. The result is a three-dimensional space in which any point has an abscissa, ordinate, and applicate.

It is logical that the fourth axis, OQ, should be perpendicular to the axes OX, OY and OZ simultaneously. But we cannot precisely construct such an axis, and therefore it remains only to try to imagine it. Each point in the four-dimensional space has four coordinates: x, y, z and q.
Now let's see how the four-dimensional cube appeared.

The picture shows a figure of one-dimensional space - the line.

If you make a parallel transfer of this line along the OY axis, and then connect the corresponding ends of the two resulting lines, you will get a square.

Similarly, if you make a parallel transfer of a square along the OZ axis and connect the corresponding vertices, you will get a cube.

And if you make a parallel transfer of the cube along the OQ axis and connect the vertices of these two cubes, then we get a four-dimensional cube. By the way, it is called a tesseract .
To draw a cube on a plane, you need to project it . It clearly looks like this:

Imagine that a frame model of a cube hangs in the air above the surface, that is, as if made of wire, and a light bulb above it. If you turn on the light bulb, draw a pencil around the shadow of the cube, and then turn off the light bulb, then the projection of the cube will be displayed on the surface.
We turn to a little more complicated. Look again at the drawing with a light bulb: as you can see, all the rays converged at one point. It is called a vanishing point and is used to construct a perspective projection (and sometimes parallel, when all the rays are parallel to each other. The result is not a sensation of volume, but it is lighter, and if the vanishing point is sufficiently far from the projected object, then the difference these two projections are hardly noticeable). To project a given point on a given plane, using the vanishing point, you need to draw a straight line through the vanishing point and this point, and then find the intersection point of the resulting straight line and plane. And in order to project a more complex shape, say, a cube, you need to project each of its vertices, and then connect the corresponding points. It should be noted that the algorithm of the projection of space on a subspace can be generalized for the case of 4D-> 3D, and not just 3D-> 2D.
As I have already said, we cannot imagine for sure exactly what the OQ axis looks like, nor does the tesseract. But we can get a limited idea of it, if we project it on volume, and then draw it on the computer screen!
Now let's talk about the tesseract projection.

On the left is the projection of the cube onto the plane, and on the right is the tesseract on the volume. They are quite similar: the projection of the cube looks like two squares, small and large, one inside the other, and whose corresponding vertices are connected by lines. A tesseract projection looks like two cubes, small and large, one inside the other, and whose corresponding vertices are connected. But we all saw a cube, and we can confidently say that a small square, a large one, and four trapeziums above, below, to the right and left of a small square are actually squares, and they are equal. And the tesseract is the same. And the big cube, and the small cube, and the six truncated pyramids on the sides of the small cube are all cubes, with what they are equal.
My program can not only draw a tesseract projection onto a volume, but also rotate it. Consider how this is done.
To begin, I'll tell you what rotation is parallel to the plane .
Imagine that a cube rotates around the axis OZ. Then each of its vertices describes a circle around the axis OZ.

And the circle is a flat figure. And the planes of each of these circles are parallel to each other, and in this case parallel to the XOY plane. That is, we can speak not only about rotation around the OZ axis, but also about rotation parallel to the XOY plane. As we see, for points that rotate parallel to the XOY axis only the abscissa and ordinate change, the applicate remains unchanged And, in fact, we we can talk about rotation around a line only when we are dealing with a three-dimensional space. In two-dimensional everything revolves around a point, in four-dimensional - around a plane, in five-dimensional space we speak about rotation around a volume. And if we can imagine a rotation around a point, then a rotation around a plane and a volume is something unthinkable. And if we talk about rotation parallel to the plane, then in any n-dimensional space a point can rotate parallel to the plane.
Many of you have probably heard of the turn matrix. Multiplying a point on it, we get a point rotated parallel to the plane by an angle phi. For two-dimensional space, it looks like this:
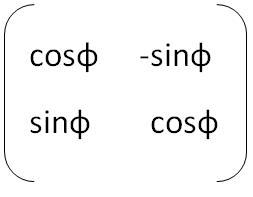
How to multiply: X of a point rotated by phi = cosine of phi * x of the original point minus sine of the angle phi * of the original point;
Yy of a point rotated by phi = sine of phi * x of the original point plus the cosine of phi * of the original point.
Xa` = cosf * Xa - sinf * Ya
Ya` = sinf * Xa + cos * Ya
where Xa and Ya are the abscissa and ordinate of the point to be rotated, Xa` and Ya` are the abscissa and ordinate of the already rotated point
For three-dimensional space, this matrix is summarized as follows:

Rotation is parallel to the XOY plane. As you can see, the Z coordinate does not change, only X and Y change.
Xa` = cosf * Xa - sinf * Ya + Za * 0
Ya` = Sinf * Xa + cosf * Ya + Za * 0
Za` = Xa * 0 + Ya * 0 + Za * 1 (in fact, Za` = Za)

Rotation is parallel to the XOZ plane. Nothing new,
Xa` = cosf * Xa + Ya * 0 - sinf * Za
Ya` = Xa * 0 + Ya * 1 + Za * 0 (in fact, Ya` = Ya)
Za` = sinf * Xa + Ya * 0 + cosf * Za

And the third matrix.
Xa` = Xa * 1 + Ya * 0 + Za * 0 (in fact, Xa` = Xa)
Ya` = Xa * 0 + cosf * Ya - sinf * Za
Za` = Xa * 0 + sinf * Ya + cosf * Za
And for the fourth dimension, they look like this:

I think you have already understood what to multiply, because I will not paint once again. But I note that it does the same thing as the matrix for turning parallel to a plane in three-dimensional space! Both this and this change only the ordinate and applicate, and do not touch the other coordinates, so it can be used in the three-dimensional case, simply ignoring the fourth coordinate.
But the projection formula is not so simple. No matter how I read the forums, none of the projection methods came up to me. Parallel did not suit me, since the projection will not look voluminous. In some projection formulas, to find the point, you need to solve a system of equations (but I don’t know how to teach a computer to solve them), I simply didn’t understand others ... In general, I decided to think of my own way. Consider for this the projection 2D-> 1D.

pov means “Point of view” (ptp) means “Point to project” (the point to be projected), and ptp` is the desired point on the OX axis.
The angles povptpB and ptpptp`A are equal as appropriate (the dotted line is parallel to the axis OX, the straight line povptp is the secant).
The x point of the ptp` is equal to the x of the ptp point minus the length of the segment ptp`A. This segment can be found from the triangle ptpptp`A: ptp`A = ptpA / tangent of the angle ptpptp`A. We can find this tangent from the triangle povptpB: the tangent of the angle ptpptp`A = (Ypov-Yptp) (Xpov-Xptp).
Answer: Xptp` = Xptp-Yptp / tangent of ptpptp`A angle.
I did not elaborate on this algorithm here, since there are a lot of special cases where the formula changes somewhat. To whom it is interesting - look in the source code of the program, everything is painted in the comments.
In order to project a point of three-dimensional space on a plane, simply consider two planes - XOZ and YOZ, and for each of them we will solve this problem. In the case of four-dimensional space, it is necessary to consider already three planes: XOQ, YOQ and ZOQ.
And finally, about the program. It works like this: initialize sixteen tesseract vertices -> depending on the commands entered by the user, rotate it -> project to volume -> depending on the commands entered by the user, rotate its projection -> project to the plane -> draw.
Projections and turns I wrote myself. They work according to the formulas that I just described. The OpenGL library draws lines, as well as mixing colors. And the coordinates of the tesseract vertices are calculated as follows:
The coordinates of the vertices of the line centered at the origin and the length of 2 - (1) and (-1);
- "-" - squares - "-" - and an edge of length 2:
(1; 1), (-1; 1), (1; -1) and (-1; -1);
- "-" - cube - "-" -:
(1; 1; 1), (-1; 1; 1), (1; -1; 1), (-1; -1; 1), (1; 1; -1), (-1; 1 ; -1), (1; -1; -1), (-1; -1; -1);
As you can see, the square is one line above the OY axis and one line below the OY axis; a cube is one square in front of the XOY plane, and one behind it; Tesseract is one cube on the other side of the XOYZ volume, and one on this. But it is much easier to perceive this alternation of units and minus ones if they are written in a column
one; one; one
-one; one; one
one; -one; one
-one; -one; one
one; one; -one
-one; one; -one
one; -one; -one
-one; -one; -one
In the first column, one and minus one alternate. In the second column, there are two plus points first, then two minuses. In the third - four plus units, and then four minus one. These were the tops of the cube. Tesseracts have twice as many of them, and therefore it was necessary to write a cycle to declare them, otherwise it is very easy to get confused.
My program can also draw anaglyph. Happy owners of 3D glasses can watch a stereoscopic image. There is nothing tricky in drawing a picture, just two projections are drawn on the plane, for the right and left eyes. But the program becomes much more visual and interesting, and most importantly - it gives a better idea of the four-dimensional world.
Less significant functions are the highlighting of one of the faces in red, so that you can better see the turns, as well as minor conveniences — adjusting the coordinates of the eye points, increasing and decreasing the speed of turning.
Archive with the program, source code and instructions for use: www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2% D0% B5% D1% 81% D1% 81% D0% B5% D1% 80% D0% B0% D0% BA% D1% 82.rar (you need to download and install the program Dropbox: www.dropbox.com )
Source: docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit
Source: https://habr.com/ru/post/180009/
All Articles