Calculating the Nth sign of Pi without calculating the previous ones
Recently, there is an elegant formula for calculating the number of Pi, which in 1995 was first published by David Bailey, Peter Borwine and Simon Plaff:
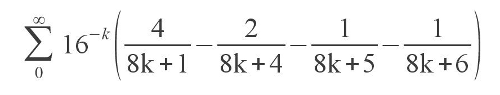
It would seem that: what is special about it is that there are a great many formulas for calculating Pi: from the Monte Carlo school method to the difficult to understand Poisson integral and the formula of François Vieta from the late Middle Ages. But it is precisely this formula that is worth paying special attention to - it allows you to calculate the nth sign of pi without finding the previous ones. For information on how this works, as well as for ready-made C language code that calculates 1,000,000th character, I ask for a habrak.
How does the algorithm for calculating the Nth pi character work?
For example, if we need the1000th hexadecimal sign of Pi, we multiply the whole formula by 16 ^ 1000, thereby turning the factor before the brackets into 16 ^ (1000-k). In exponentiation, we use the binary exponentiation algorithm or, as will be shown in the example below, exponentiation modulo . After that, we calculate the sum of several members of the series. Moreover, it is not necessary to calculate a lot: as k increases, 16 ^ (Nk) decreases rapidly, so that subsequent terms will not affect the value of the desired digits). That's all the magic - ingenious and simple.
The Bailey-Borwein-Plaff formula was found by Simon Plaff using the PSLQ algorithm , which was included in the Top 10 Algorithms of the Century list in 2000. The very same PSLQ algorithm was in turn developed by Bailey. Here is a Mexican series about mathematicians.
By the way, the running time of the algorithm is O (N), memory usage is O (log N), where N is the sequence number of the desired character.
')
I think it would be appropriate to give the code in C written by the author of the algorithm, David Bailey:
What opportunities does it provide? For example: we can create a distributed computing system that calculates the Pi number and set all Habrom a new record in the accuracy of the calculation (which now, by the way, is 10 trillion decimal places). According to empirical data, the fractional part of Pi is a normal numeric sequence (although it has not yet been reliably proven), which means that a sequence of digits from it can be used in generating passwords and just random numbers, or in cryptographic algorithms (for example, in hashing) . You can find a great many ways to use it - you just need to turn on the fantasy.
More information on the topic can be found in the article by David Bailey, where he tells in detail about the algorithm and its implementation ( pdf );
And, it seems, you have just read the first Russian-language article about this algorithm in Runet - I could not find others.
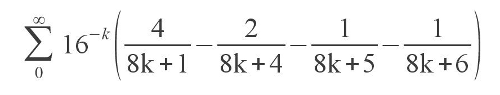
It would seem that: what is special about it is that there are a great many formulas for calculating Pi: from the Monte Carlo school method to the difficult to understand Poisson integral and the formula of François Vieta from the late Middle Ages. But it is precisely this formula that is worth paying special attention to - it allows you to calculate the nth sign of pi without finding the previous ones. For information on how this works, as well as for ready-made C language code that calculates 1,000,000th character, I ask for a habrak.
How does the algorithm for calculating the Nth pi character work?
For example, if we need the
The Bailey-Borwein-Plaff formula was found by Simon Plaff using the PSLQ algorithm , which was included in the Top 10 Algorithms of the Century list in 2000. The very same PSLQ algorithm was in turn developed by Bailey. Here is a Mexican series about mathematicians.
By the way, the running time of the algorithm is O (N), memory usage is O (log N), where N is the sequence number of the desired character.
')
I think it would be appropriate to give the code in C written by the author of the algorithm, David Bailey:
/* This program implements the BBP algorithm to generate a few hexadecimal digits beginning immediately after a given position id, or in other words beginning at position id + 1. On most systems using IEEE 64-bit floating- point arithmetic, this code works correctly so long as d is less than approximately 1.18 x 10^7. If 80-bit arithmetic can be employed, this limit is significantly higher. Whatever arithmetic is used, results for a given position id can be checked by repeating with id-1 or id+1, and verifying that the hex digits perfectly overlap with an offset of one, except possibly for a few trailing digits. The resulting fractions are typically accurate to at least 11 decimal digits, and to at least 9 hex digits. */ /* David H. Bailey 2006-09-08 */ #include <stdio.h> #include <math.h> int main() { double pid, s1, s2, s3, s4; double series (int m, int n); void ihex (double x, int m, char c[]); int id = 1000000; #define NHX 16 char chx[NHX]; /* id is the digit position. Digits generated follow immediately after id. */ s1 = series (1, id); s2 = series (4, id); s3 = series (5, id); s4 = series (6, id); pid = 4. * s1 - 2. * s2 - s3 - s4; pid = pid - (int) pid + 1.; ihex (pid, NHX, chx); printf (" position = %i\n fraction = %.15f \n hex digits = %10.10s\n", id, pid, chx); } void ihex (double x, int nhx, char chx[]) /* This returns, in chx, the first nhx hex digits of the fraction of x. */ { int i; double y; char hx[] = "0123456789ABCDEF"; y = fabs (x); for (i = 0; i < nhx; i++){ y = 16. * (y - floor (y)); chx[i] = hx[(int) y]; } } double series (int m, int id) /* This routine evaluates the series sum_k 16^(id-k)/(8*k+m) using the modular exponentiation technique. */ { int k; double ak, eps, p, s, t; double expm (double x, double y); #define eps 1e-17 s = 0.; /* Sum the series up to id. */ for (k = 0; k < id; k++){ ak = 8 * k + m; p = id - k; t = expm (p, ak); s = s + t / ak; s = s - (int) s; } /* Compute a few terms where k >= id. */ for (k = id; k <= id + 100; k++){ ak = 8 * k + m; t = pow (16., (double) (id - k)) / ak; if (t < eps) break; s = s + t; s = s - (int) s; } return s; } double expm (double p, double ak) /* expm = 16^p mod ak. This routine uses the left-to-right binary exponentiation scheme. */ { int i, j; double p1, pt, r; #define ntp 25 static double tp[ntp]; static int tp1 = 0; /* If this is the first call to expm, fill the power of two table tp. */ if (tp1 == 0) { tp1 = 1; tp[0] = 1.; for (i = 1; i < ntp; i++) tp[i] = 2. * tp[i-1]; } if (ak == 1.) return 0.; /* Find the greatest power of two less than or equal to p. */ for (i = 0; i < ntp; i++) if (tp[i] > p) break; pt = tp[i-1]; p1 = p; r = 1.; /* Perform binary exponentiation algorithm modulo ak. */ for (j = 1; j <= i; j++){ if (p1 >= pt){ r = 16. * r; r = r - (int) (r / ak) * ak; p1 = p1 - pt; } pt = 0.5 * pt; if (pt >= 1.){ r = r * r; r = r - (int) (r / ak) * ak; } } return r; } What opportunities does it provide? For example: we can create a distributed computing system that calculates the Pi number and set all Habrom a new record in the accuracy of the calculation (which now, by the way, is 10 trillion decimal places). According to empirical data, the fractional part of Pi is a normal numeric sequence (although it has not yet been reliably proven), which means that a sequence of digits from it can be used in generating passwords and just random numbers, or in cryptographic algorithms (for example, in hashing) . You can find a great many ways to use it - you just need to turn on the fantasy.
More information on the topic can be found in the article by David Bailey, where he tells in detail about the algorithm and its implementation ( pdf );
And, it seems, you have just read the first Russian-language article about this algorithm in Runet - I could not find others.
Source: https://habr.com/ru/post/179829/
All Articles