Russian Code Cup 2013 - analysis of tasks of the 2nd qualification round

That was the second qualifying round of the Russian Code Cup. May holidays, many who went somewhere ... However, in order to qualify for the qualifying round, the participants of the second qualifying round had to fight.
As in the previous round, there were more registered people than those who sent the decisions. Therefore, among those who took part, we reflect only those who sent at least one decision.
May heat and 5 tasks that need to be solved in 2 hours:

• task A. Molecule
• Problem B. Sea battle
• task C. Cork
• Problem D. Table
• Task E. Space Expedition

Conditions and solution - under the cut.

Some statistics on the results of the second qualification.
Authorized during the round of 735 people. Of these, at least one solution was sent by 536 people.
A total of 2707 solutions were sent.
Here are the nicknames of the participants who first sent the correct problem solution (in brackets - the time after the start of the round in minutes and seconds)

• Problem A: Rayblast (2:56)
• Problem B: Milanin (14:58)
• Problem C: KAN (20:27)
• Problem D: XopEka (51:58)
• Task E: maria.sharapova (18:45)

The territorial distribution of participants in this round was as follows:
Russia => 343
Ukraine => 78
Belarus => 29
United States => 22
Kazakhstan => 16
Armenia => 8
Poland => 5
Azerbaijan => 4
Uzbekistan => 4
Ireland => 3
Georgia => 3
Kyrgyzstan => 3
Sweden => 2
United Kingdom => 2
Germany => 2
Moldova => 2
Iceland => 1
Belgium => 1
Pakistan => 1
Latvia => 1
Republic of Korea => 1
Spain => 1
China => 1
Czech Republic => 1
Switzerland => 1
Canada => 1
In the qualifying round, as in the previous round, there were 201 people.

1. Mikhail Kolupaev
2. Evgeny Sobolev
3. Andrey Grinenko
4. Evgeny Kapun
5. Denis Dublennykh
6. Alexey Safronov
7. Vladislav Simonenko
8. Andriy Pavlisko
9. Yegor Suvorov
10. Pavel Mavrin

And now we will consider the analysis of tasks (analysis is also available on the site of the Russian Code Cup ).
Recall that there is the last, 3rd qualifying round. If you want to take part in the final, then hurry to pass the latest qualification to be able to compete in the qualifying round.

Task A. Molecule
Idea: Vitaly Aksenov
Condition: Anna Malova
Realization: Andrey Komarov
Analysis: Anna Malova

The task
Time limit - 2 seconds
Memory limit - 256 megabytes
As a result of recent research in the top-secret laboratory, a new substance was discovered. Each molecule of this substance represents a cycle consisting of two types of atoms, which we will conventionally call black and white (the real names of the atoms are kept in strict secret). To carry out a top-secret reaction, it is necessary to transfer the molecule to an unstable state, in which it can break up into two independent molecules, each of which consists of only one type of atoms.
Studies have shown that a molecule disintegrates if all atoms of each color form a continuous block.
To rebuild the molecule, scientists can perform the following operation: a continuous sequence of atoms is cut from the cycle and inserted into another place. An example of the rebuilding of the molecule is shown in the figure.

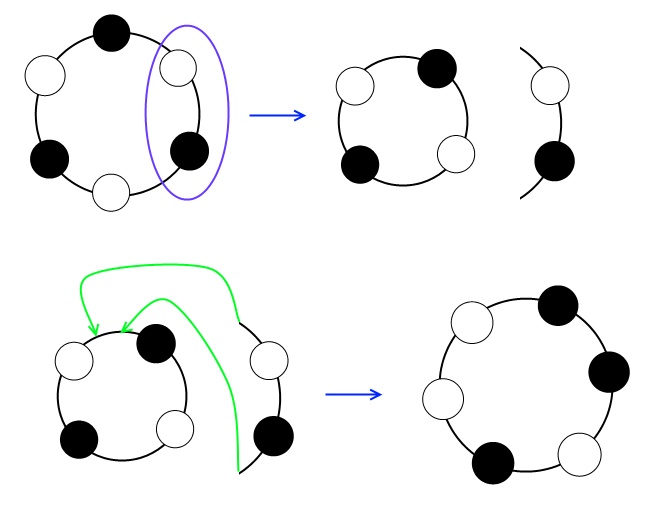
Now scientists are trying to figure out the minimum number of operations described can lead to a molecule in an unstable state. Help them figure it out.

Input Format	The first line of the input file contains a natural number n - the number of molecules that must be investigated. Each of the following n lines contains the description of one molecule in the following format: a line consisting of at least three letters w and b, denoting white and black atoms, respectively. It is guaranteed that each letter is found in each molecule at least once. The total length of all molecules does not exceed 200,000.
Output format	Print n lines. In the i-th line print the minimum number of operations that must be performed in order for the ith molecule to become unstable.
Examples	Input data Output 3 wbbw wbbwb wbwbwb 0 one 2

')
Parsing

Denote by m the number of blocks of the same color in a molecule. Note that m is even, and the number of black and white blocks is the same. From the obvious fact that the piece has two ends, and it touches two blocks, it follows that with each reorganization of the molecule the number of blocks of each color will decrease by no more than one. To reduce the number of blocks of each color by exactly one can be as follows: cut one block and embed it in the middle of another block of the same color. Thus, total scientists need m / 2 - 1 operations.
O time (molecule length).

Problem B. Sea battle
Idea: Vitaly Aksyonov
Realization: Boris Minaev
Analysis: Boris Minaev

The task
Time limit - 2 seconds
Memory limit - 256 megabytes
Petya and Vasya play a sea battle with slightly modified rules. Vasya has already lost ten games in a row and does not intend to lose again. He analyzed the tactics of Petit’s battle and found a significant flaw in it (at least, he hopes so strongly). It turned out that the field has a rectangle of area A on B cells, which Petya for all ten games never shot. Therefore, Vasya decided to take three of his largest ships and place them in this rectangle.
Vasya’s plans, of course, are far-reaching, but he still needs to deal with some minor problems first. For example, he needs to find out if he can still arrange his three ships so that they fit completely into a given rectangle. According to the rules, ships are rectangles that need to be placed parallel to the sides of the field. Ships allowed to rotate 90 degrees. Ships can touch each other, but they should not have common cells of the field.

Input Format	The first line contains an integer t (1 ≤ t ≤ 105) - the number of tests. The description of each test consists of 4 lines. In the first of them are two integers A and B (1 ≤ A, B ≤ 109) - the size of the rectangle in which you want to place the ships. The next three lines contain two integers ai and bi (1 ≤ ai, bi ≤ 109) - the dimensions of the i-th ship.
Output format	You need to print t lines that are answers to tests from the input data. For each test, output Yes if the ships can be placed, and No otherwise.
Examples	Input data Output 2 7 7 6 3 6 1 3 3 4 4 5 1 eleven 12 Yes No

Parsing

Suppose we found an arrangement of rectangles that satisfies the condition. Then there is a line parallel to some side of a large rectangle — such that one of the small rectangles will be completely on one side of it, and the other two on the other. Let us leave proof of this fact as an exercise.
We take advantage of this fact. Let's look through all the possible turns of the rectangles (including the big ones) - there are only 16. If there is a correct arrangement, then there is a horizontal line (at least for one of the turns) that separates the rectangles. Let's look through the rectangle that will be below this line and divide the large rectangle into two parts by a horizontal line. It remains to make sure that the selected rectangle fits in a large width, and the other two can be placed in the upper part.
If at least in one of the cases we were able to place the rectangles, then the answer is Yes, otherwise - No.

Problem C. Cork
Idea: Vitaly Aksenov
Realization: Nikolay Vedernikov
Analysis: Nikolay Vedernikov

The task
Time limit - 2 seconds
Memory limit - 256 megabytes
In 2050, overtaking was prohibited on all roads in order to improve road safety. Moreover, it is forbidden to approach the car in front closer than L meters. The observance of the rules is monitored by video cameras placed on all roads. Unfortunately, these measures did not fully help in the fight against traffic jams.
Professor Svinkin every morning gets from home to work. The road he rides is straight. We introduce on it a coordinate system with a unit equal to a meter, and we will represent machines by segments on this straight line, which move in the direction of increasing the coordinate.
Initially, the professor's car is located at the beginning of the road, so its front point is at the origin. The maximum speed of the professor’s machine is V meters per second.
In addition to the professor's car, there are n more cars on the road that move along the road. When driving, each car tries to move with its maximum speed. When machine A catches up with the vehicle B in front, so that the front point A is exactly L from the rear point B, machine A instantly reduces its speed to speed B and then repeats all changes in speed B. No car leaves the road.
Find the time for which Professor Svinkin gets to his work. It is believed that this happened if the front point of his car was at the point with coordinate S.

Input Format	The input to the task contains several test cases. The description of each set consists of several lines. The first line of the description contains four integers: n, L, S and V (1 ≤ n ≤ 10000, 1 ≤ L ≤ 1000, 1 ≤ S ≤ 109, 1 ≤ V ≤ 100) - the number of cars in front of the professor, the minimum distance between the machines in meters, the distance from home to the professor's place of work and the maximum speed of the professor's car in meters per second. The next n line contains three integers xi, li and vi (1 ≤ xi ≤ 109, 1 ≤ li ≤ 10, 1 ≤ vi ≤ 100) - the coordinate of the front point of the i-th machine at the initial moment of time, its length and maximum speed in meters per second. It is guaranteed that the machines are set in the order of removal of the professor’s machine, and that the distance between two neighboring machines at the initial time is not less than L meters. The last line of the test contains four zeros. The total number of cars in all tests does not exceed 10,000
Output format	For each test request, print on a separate line the time it takes the professor to work, in seconds. The answer should be displayed with an absolute or relative error of no more than 10−5.
Examples	Input data Output 1 1 10 2 3 1 1 1 1 10 1 3 2 1 1 1 10 2 3 1 2 2 3 15 3 4 1 2 10 3 1 1 3 500 93 123 3 2 0 0 0 0 9.0000000000 10.0000000000 5.0000000000 15.00000000 191.5000000000

Parsing
In the task it was required to find out in how many minutes the professor would arrive at his work. When one car catches up with another, it starts to go after it at the same speed. Then we can assume that the first machine is len _first + L + len _second , and the second is not. Consider the moment in time when the i-th machine will catch up with (i + 1) -th, but if it does not catch up with her, we will assume that this moment will occur at infinity. Also consider the point in time when the professor's car will reach the finish. Choose an event that happens before everything else. Add the time after which it will occur to the answer. If this event is the arrival to the finish line of the professor's car, then the problem is solved. Otherwise, combine the machines according to the rule described above and solve the problem of a smaller dimension. This phase is done in O (n). All such phases are not more than n.
Total operation time O (n ² ). Using various data structures, this solution can be accelerated to O (n log n) and even to O (n).

Problem D. Table
Idea: Vitaly Aksyonov
Realization: Vitaly Aksyonov
Analysis: Vitaly Aksyonov

The task
Time limit - 2 seconds
Memory limit - 256 megabytes
Consider a rectangular table composed of n × m cells. Each cell is allowed to paint in black or white. A coloring is called correct if there are no four cells of the same color, the centers of which are located in the corners of a non-degenerate rectangle with sides parallel to the sides of the table.
It is required to count the number of different correct colorings of the rectangle. Since this number can be large, it is necessary to derive it by the given module r.
For example, for a 2 × 2 rectangle, the number of such colorings is 14: all colors are suitable, except for those with all four cells painted in one color.

Input Format	The first line of the input file contains a positive integer t - the number of tests (1 ≤ t ≤ 150). Each of the following t lines contains 3 integers: n, m and r - the size of the table and the module for which you want to display the answer. (1 ≤ n, m, r ≤ 1018)
Output format	For each test request print the answer on a separate line.
Examples	Input data Output 2 1 1 2 2 2 1000000 0 14

Parsing
We denote the minimum side of the rectangle n, and the maximum - m. We arrange the table with the long side horizontally and, accordingly, we will call the shorter rows as columns.
3 cases should be examined:
• n = 1. Then the answer will be 2 ^m .
• n = 2. We can only afford two one-color columns - one black and the other white. All other columns must be two-color, that is, each has two options. Hence, the answer is C _m ² • 2 ^{m - 1} + C _m ¹ • 2 ^m + 2 ^m .
• n> 2. You can see that if m> 6, then there is not a single good coloring. Indeed, the coloring of the first column with the coloring of the second can coincide only in two places. Similarly, with the coloring of the first and third. And if m> 6, then the coloring of the second and third ones coincide in at least three places. And this means that there is no good coloring. After we have limited the size of the table, it is easy to understand that it’s time for the rest to work through the search.

Task E. Space Expedition
Idea: Vitaly Aksenov
Realization: Pavel Krotkov
Analysis: Pavel Krotkov

The task
Time limit - 2 seconds
Memory limit - 256 megabytes
In 2345, humanity had the opportunity to send the first space expedition to the distant planet Nutpen. The road to it is long and full of dangers, so it was decided to send n spacecraft of various types to it at once.
Each ship can operate on one of two different types of fuel. Since the ships are different, fuel consumption may also vary. In this case, in flight, the ship must use only one of the two types of fuel, it is impossible to switch from one to another in space.
About ship number i, it is known that he will spend either ai kilotons of the first type of fuel, or bi kilotons of the second type of fuel on the way to the planet Nuthen. By virtue of the design features of the ships, for any of them the equality ai + bi = 4k holds, and the number k is the same for all ships.
At the disposal of the expedition command there are exactly k (n + 1) kilotons of fuel of the first type and the same kilotons of fuel of the second type. Now you need to decide on what type of fuel each of the ships will fly to the planet Nutpen.

Input Format	The first line contains a single integer t - the number of input data sets in the test. The following is a description of the input data sets themselves. The first line of the description of the next set of input data contains an integer n (1 ≤ n ≤ 105) - the number of ships that fly to the planet Nutpen. The next n lines contain two integer non-negative numbers ai and bi - the amount of fuel of the first and second type, necessary for the respective ship. It is guaranteed that the sum of ai and bi is the same for all ships, is a multiple of four and does not exceed 108. The sum n in all sets in one test does not exceed 500,000.
Output format	For each set of input data, output a single line consisting of n characters, in which the character number i is the character '1', if ship i must fly on Nutpen using the first type of fuel, and the character '2' if it needs to use fuel second type. The amount of required fuel of each type should not exceed k (n + 1). If there are several possible answers, output any of them. It is guaranteed that the answer always exists.
Examples	Input data Output 2 five 13 3 1 2 2 4 0 0 4 one 4 4 12221 2

Parsing
We sort all the ships by the amount of fuel of the first type that they need. Then we choose the maximum t - such that the sum ai of the first t ships does not exceed k (n + 1). These t ships will use fuel of the first type, and all the rest will use fuel of the second type.

Let us prove that this algorithm will always find the answer under the conditions set in the problem. Note that the sum _{i = 1} ^{t + 1} a _i > n • (k + 1). Hence, for any i> t, we have a _i > (n + 1) / (t + 1). Therefore, we obtain that for any i> t, b _i <4k - (n + 1) / (t + 1) holds. It remains to prove that the second amount does not exceed the stated expression. ∑ _{i = t + 1 ⁿ} b _i <(n - (t + 1) + 1) • (4k - (n + 1) / (t + 1)) ≤ (n + 1) k. The last inequality, after opening the brackets, turns into the inequality "arithmetic mean minus geometric mean". Hence, the above algorithm will always find a solution.

Recall that there is the last, third qualifying round. If you want to participate in the final, hurry up to register for the latest qualification to be able to compete in the qualifying round.