Vain attempts to win the lottery
Imagine an imaginary cunning uncle who wants to cheat and make money on the "mugs". Let's call him Gennady Obmanuev.
On the most usual Tuesday, Gennady Obmanuyev suddenly got a brilliant idea: to create a lottery in which each player can indicate his chance of winning and, consequently, the win multiplier and play the rules set by him! In order to always stay in the black, Gennady at the end of each successful game takes a nominal fee of 5% of the winnings.
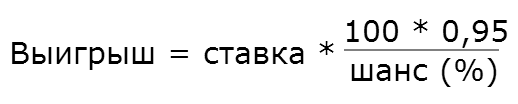
* briefly about the game
As in the case of a casino, the longer a player plays such a game, the more likely he is to lose in the end. But is it really impossible to deceive a cunning uncle by inventing wonderful tactics, thanks to which you can increase your chances of winning?
To begin with, let's try the standard tactics in any undertakings: a hundred thousand iterations with random values. On average, this will show the results of a huge mass of people who do not play systematically. Naturally, it is unreasonable to set 100% on a percent with a 5% tax, so we limit the rates from 10% (called Gennady minimum) to 94%.
')
I only know php, so I’ll write on it, I think it’s quite clear to everyone:
The results were predictable, but not systematic because of the huge amount of randomness in the game.
I launched this cycle five times, I got the results:
The results look deplorable: our players owed a sly uncle ~ 25 original money. On average, players lose in 100,000 iterations of ~ 250,000 conventional units. Let's try to add logic to our algorithm. Naturally, the most reasonable would be to write
at the beginning of the cycle, but we are not looking for easy ways! Let's start with changing random values. Let's try to play with strictly set values. For example, the minimum bid for the maximum chance. What will lead such tactics?
As a result, we, of course, lose a lot less, because we bet less! Although you can see that the loss has become more predictable. It hovers around 50,000, with virtually no scatter.
The size of the loss is not so important if we lose dozens of initial amounts and owe the cunning Gennady. I specifically do not change the algorithm in the direction of "time to stop", because I wonder if it is possible to get positive results after 100,000 iterations.
Let's try to play with the minimum bet and the minimum chance to win.
Again we lose. This time the spread is very large, and this is logical: after all, we play with a minimum chance of winning.
By the way, what is interesting: if the minimum rate in the lottery would be 0.1%, then the results would be as follows:
The multiplier is so small that it increases our rate almost a thousand times, but this happens so infrequently that the results are completely unpredictable.
Let's try to apply some algorithm to win. For example: the more money we won, the more risky we can play. I implemented it this way:
* hope it works
And it also didn't work out for me, the scatter of results was great, but in any case I lost.
Then I tried to take serious measures by organizing an “inside pocket”. There the player adds money that he would not spend for anything to stay with at least some pennies. I had to change the logic, because now the attempts will be clearly less than 100,000. And the most important thing I did: I set a goal for the player. For example, double the winnings.
And only in this situation, with some probability, I began to win relatively small amounts. However, play too.
In games where the percentage goes to the "institution" or to the cunning Gennady Obmanuyev, I did not manage to win a large number of people during a long game, and I doubt that this is possible. In any case, due to the fact that events occur by chance, and the lottery takes the win in any case, it always remains in the black. The tax in this case fulfills the same goal as Zero on the roulette at the casino: it shifts the overall chance of winning towards the institution, not the player.
Report errors in the text and in the code logic, please, in private messages. I will promptly correct.
By the way, can someone come up with an algorithm that still wins in this lottery? It would be very interesting. What is the best algorithm in this game?
On the most usual Tuesday, Gennady Obmanuyev suddenly got a brilliant idea: to create a lottery in which each player can indicate his chance of winning and, consequently, the win multiplier and play the rules set by him! In order to always stay in the black, Gennady at the end of each successful game takes a nominal fee of 5% of the winnings.
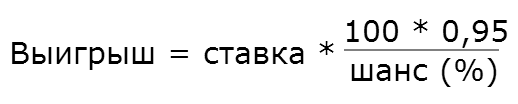
* briefly about the game
As in the case of a casino, the longer a player plays such a game, the more likely he is to lose in the end. But is it really impossible to deceive a cunning uncle by inventing wonderful tactics, thanks to which you can increase your chances of winning?
To begin with, let's try the standard tactics in any undertakings: a hundred thousand iterations with random values. On average, this will show the results of a huge mass of people who do not play systematically. Naturally, it is unreasonable to set 100% on a percent with a 5% tax, so we limit the rates from 10% (called Gennady minimum) to 94%.
')
I only know php, so I’ll write on it, I think it’s quite clear to everyone:
<?php $bank = 1000000000; // define('START_MONEY', 10000); $money = START_MONEY; // for($i = 0; $i < 100000; $i++){ $bet = mt_rand(10, 100); // = 10. $chance = mt_rand(10, 94); //94+ - $random = mt_rand(1, 100); $money -= $bet; $bank += $bet; // if($chance >= $random){ $money += $bet * 95/$chance; // :) $bank -= $bet * 100/$chance; // :) } } echo floor($money-START_MONEY); The results were predictable, but not systematic because of the huge amount of randomness in the game.
I launched this cycle five times, I got the results:
- Player loses 225043.
- Player loses 272766.
- Player loses 320369.
- Player loses 276055.
- Player loses 254899.
The results look deplorable: our players owed a sly uncle ~ 25 original money. On average, players lose in 100,000 iterations of ~ 250,000 conventional units. Let's try to add logic to our algorithm. Naturally, the most reasonable would be to write
break; at the beginning of the cycle, but we are not looking for easy ways! Let's start with changing random values. Let's try to play with strictly set values. For example, the minimum bid for the maximum chance. What will lead such tactics?
$bet = 10; $chance = 94; As a result, we, of course, lose a lot less, because we bet less! Although you can see that the loss has become more predictable. It hovers around 50,000, with virtually no scatter.
- Player loses 50940.
- Player loses 50900.
- Player loses 51274.
- Player loses 51041.
- Player loses 49344.
The size of the loss is not so important if we lose dozens of initial amounts and owe the cunning Gennady. I specifically do not change the algorithm in the direction of "time to stop", because I wonder if it is possible to get positive results after 100,000 iterations.
Let's try to play with the minimum bet and the minimum chance to win.
$bet = 10; $chance = 10; Again we lose. This time the spread is very large, and this is logical: after all, we play with a minimum chance of winning.
- Player loses 37650.
- Player loses 58075.
- Player loses 52660.
- Player loses 43635.
- Player loses 40310.
By the way, what is interesting: if the minimum rate in the lottery would be 0.1%, then the results would be as follows:
- Player Wins 83,000!
- Player loses 78500.
- Player loses 12,000.
- Player Wins 7000!
- Player loses 69,000.
The multiplier is so small that it increases our rate almost a thousand times, but this happens so infrequently that the results are completely unpredictable.
Let's try to apply some algorithm to win. For example: the more money we won, the more risky we can play. I implemented it this way:
$bank = 1000000000; // define('START_MONEY', 10000); $money = START_MONEY; // for($i = 0; $i < 100000; $i++){ $bet = 10; $pre_chance = 100 * (2 - 0.94 * $money/START_MONEY); //94+ - if($pre_chance > 94){ $chance = 0.94; }else{ $chance = $pre_chance; } $random = mt_rand(1, 1000)/10; $money -= $bet; $bank += $bet; // if($chance >= $random){ $money += $bet * 95/$chance; // :) $bank -= $bet * 100/$chance; // :) } } echo floor($money-START_MONEY); * hope it works
And it also didn't work out for me, the scatter of results was great, but in any case I lost.
Then I tried to take serious measures by organizing an “inside pocket”. There the player adds money that he would not spend for anything to stay with at least some pennies. I had to change the logic, because now the attempts will be clearly less than 100,000. And the most important thing I did: I set a goal for the player. For example, double the winnings.
$bank = 1000000000; // define('START_MONEY', 10000); $money = START_MONEY; // $pocket = $money/2; $money /= 2; $goal = START_MONEY*2; for($i = 0; $i < 100000; $i++){ if($money < START_MONEY/10){ break; //... } if($money + $pocket >= $goal){ break; //! } $bet = mt_rand(10, $money/10); // = 10. $chance = mt_rand(10, 94); //94+ - $random = mt_rand(1, 100); $money -= $bet; $bank += $bet; // if($chance >= $random){ $money += $bet * 95/$chance / 2; // :) $pocket += $bet * 95/$chance / 2; // :) $bank -= $bet * 100/$chance; // :) } } echo floor($money-START_MONEY); And only in this situation, with some probability, I began to win relatively small amounts. However, play too.
Conclusion
In games where the percentage goes to the "institution" or to the cunning Gennady Obmanuyev, I did not manage to win a large number of people during a long game, and I doubt that this is possible. In any case, due to the fact that events occur by chance, and the lottery takes the win in any case, it always remains in the black. The tax in this case fulfills the same goal as Zero on the roulette at the casino: it shifts the overall chance of winning towards the institution, not the player.
Report errors in the text and in the code logic, please, in private messages. I will promptly correct.
By the way, can someone come up with an algorithm that still wins in this lottery? It would be very interesting. What is the best algorithm in this game?
Source: https://habr.com/ru/post/179639/
All Articles