Quantum teleportation: is data transfer faster than the speed of light?
Good day.
I noticed the public interest in the issue of quantum teleportation in particular and in quantum mechanics in general. This post is a moderately simplified explanation of the basics of quantum mechanics and teleportation from the point of view of quantum information. That is, stories about how to teleport a ray of light at home using blue electrical tape and DVD-drive will not.
Anyone who understands the quantum communication protocols - I ask in the comments to discuss the problems and their solutions.
First, let's introduce the basic concepts:
To better understand what this is and how it works, let's take for example the simplest quantum system consisting of one photon with spin up:
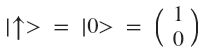
This is quite such an ordinary photon, which can be produced in any laboratory. Notice that I recorded the state of the spin-up photon as the vector of the qubit 0 in the base
: the photon spin will be a qubit (quantum bit of information) in our journey through the quantum world.
')
Now let's introduce this system into a superposition state using the Hadamard transform :
Next, let's measure the spin of our photon. As mentioned earlier, the measurement will be carried out in the database
:
This is the state of quantum superposition: before the measurement, the system is in several states of the base at the same time (ie, the state vector of the system is equal to the sum of the vectors of the base with different coefficients), and during the measurement it “collapses” into one of the states of the base with some by probability. No magic, just numbers.
Now let's see what quantum entanglement is. To do this, we need to introduce the concept of a tensor product:
Two entangled photons form a system whose state can be expressed, for example, as follows:
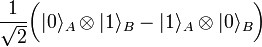
I will not explain which system is called confusing (it will be released very long and not very clear), you can read about it on Wikipedia . Instead, let's see how remarkable such a system is.
Suppose I want to see the probability of finding this system in a state
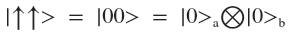
that is, when two photons have a spin
:
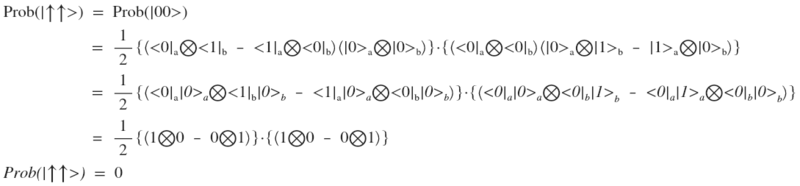
A similar result is obtained when calculating the probability of obtaining two entangled photons in the state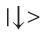
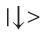. However, if we calculate the probability of obtaining a photon in a state and photon b able (i.e. general system state 
) we get a probability of 1/2.
What does it mean? This means that having a system of two entangled photons, having measured the state of one of them, we know for sure the state of the second, no matter what distance they are from each other.
Looking at the basics of quantum mechanics, we can move on to quantum teleportation.
Greet our old acquaintances, Alice and Bob.
So, Alice and Bob have a synchronized clock and a pair of entangled photons: one is for Alice, the other is for Bob. Alice measures the state of her photon, and gets
(with a probability of 0.5, as we saw earlier). At the same time photon Bob takes the state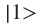 
. After time T (so as not to get ahead of Alice) Bob takes measurements on his photon, and understands what measurement result Alice received.
The problem here is very simple and obvious: Alice cannot control the state of her photon after measurement.
Suppose Alice wants to transfer the following bit sequence to Bob: “011001”. To do this, he and Bob will need 6 pairs of entangled photons. Alice takes measurements of all six, and gets the following result: "010111". Accordingly, Bob receives "101000", will apply the XOR operation in order to obtain the sequence that was obtained from Alice: "010111". However, Bob does not know which sequence Alice wanted to convey. In order to completely restore the transmitted message on the side of Bob, Alice should send him information on the errors received by her on the classical channel: “001110”. After receiving this information, Bob can easily restore Alice’s message: “011001”.
As we see, the use of a quantum classical channel for data transmission is inevitable. What are the advantages of such a transfer, you ask? Quantum transmission eliminates the possibility of Man in the middle attack: even if the error information is intercepted, it will not help the attacker to know the transmitted message. The only thing an attacker can do is to change the error information, but this also has protection that uses quantum properties.
But more about that another time.
I noticed the public interest in the issue of quantum teleportation in particular and in quantum mechanics in general. This post is a moderately simplified explanation of the basics of quantum mechanics and teleportation from the point of view of quantum information. That is, stories about how to teleport a ray of light at home using blue electrical tape and DVD-drive will not.
Anyone who understands the quantum communication protocols - I ask in the comments to discuss the problems and their solutions.
Fundamentals of Quantum Mechanics
First, let's introduce the basic concepts:
- The state of a system in quantum mechanics is represented by a vector. Recording is done by Dirac notation .
- The states of the system after measurement (that is, the state that we see from the outside) represent an orthonormal base. In other words, measurements take place in an orthonormal state database.
- Measurement is nothing more than the projection of the state vector of the system on one of the vectors of the measuring base:
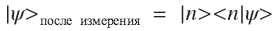
- Probability that the system
will be projected onto the vector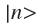 
:
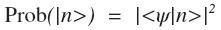
To better understand what this is and how it works, let's take for example the simplest quantum system consisting of one photon with spin up:
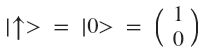
This is quite such an ordinary photon, which can be produced in any laboratory. Notice that I recorded the state of the spin-up photon as the vector of the qubit 0 in the base
: the photon spin will be a qubit (quantum bit of information) in our journey through the quantum world.')
Now let's introduce this system into a superposition state using the Hadamard transform :
- Transformation matrix:
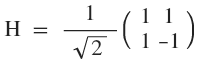
- System status after conversion:
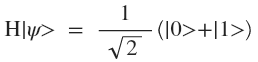
Next, let's measure the spin of our photon. As mentioned earlier, the measurement will be carried out in the database
:- Probability of getting :
- Probability of getting :
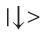This is the state of quantum superposition: before the measurement, the system is in several states of the base at the same time (ie, the state vector of the system is equal to the sum of the vectors of the base with different coefficients), and during the measurement it “collapses” into one of the states of the base with some by probability. No magic, just numbers.
Now let's see what quantum entanglement is. To do this, we need to introduce the concept of a tensor product:
Tensor product of states of two photons
We take two photons, the states of which we will describe in two Gilbert spaces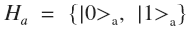 
and 
. The tensor product of these spaces will be
In the same space will be described a system consisting of two backgrounds, one of which belongs to the space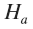
, and second - 
.
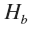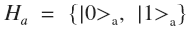and . The tensor product of these spaces will beIn the same space will be described a system consisting of two backgrounds, one of which belongs to the space
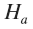, and second - 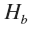.Two entangled photons form a system whose state can be expressed, for example, as follows:
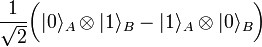
I will not explain which system is called confusing (it will be released very long and not very clear), you can read about it on Wikipedia . Instead, let's see how remarkable such a system is.
Suppose I want to see the probability of finding this system in a state
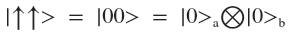
that is, when two photons have a spin
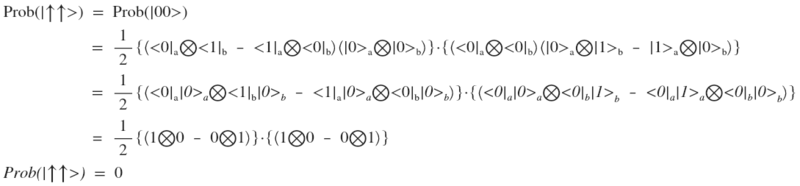
:A similar result is obtained when calculating the probability of obtaining two entangled photons in the state
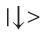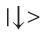. However, if we calculate the probability of obtaining a photon in a state and photon b able (i.e. general system state ) we get a probability of 1/2.What does it mean? This means that having a system of two entangled photons, having measured the state of one of them, we know for sure the state of the second, no matter what distance they are from each other.
Looking at the basics of quantum mechanics, we can move on to quantum teleportation.
Quantum teleportation
Greet our old acquaintances, Alice and Bob.
So, Alice and Bob have a synchronized clock and a pair of entangled photons: one is for Alice, the other is for Bob. Alice measures the state of her photon, and gets
(with a probability of 0.5, as we saw earlier). At the same time photon Bob takes the state 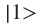. After time T (so as not to get ahead of Alice) Bob takes measurements on his photon, and understands what measurement result Alice received.The problem here is very simple and obvious: Alice cannot control the state of her photon after measurement.
Suppose Alice wants to transfer the following bit sequence to Bob: “011001”. To do this, he and Bob will need 6 pairs of entangled photons. Alice takes measurements of all six, and gets the following result: "010111". Accordingly, Bob receives "101000", will apply the XOR operation in order to obtain the sequence that was obtained from Alice: "010111". However, Bob does not know which sequence Alice wanted to convey. In order to completely restore the transmitted message on the side of Bob, Alice should send him information on the errors received by her on the classical channel: “001110”. After receiving this information, Bob can easily restore Alice’s message: “011001”.
As we see, the use of a quantum classical channel for data transmission is inevitable. What are the advantages of such a transfer, you ask? Quantum transmission eliminates the possibility of Man in the middle attack: even if the error information is intercepted, it will not help the attacker to know the transmitted message. The only thing an attacker can do is to change the error information, but this also has protection that uses quantum properties.
But more about that another time.
Source: https://habr.com/ru/post/179443/
All Articles