Quickly squaring numbers from 1 to 100
Inspired by this article, I decided to share with you a quick squaring method. Squaring is a rarer operation than multiplying numbers, but there are some interesting rules for it.

* squares to hundreds
In order to thoughtlessly not square all the numbers using a formula, you need to maximally simplify your task with the following rules.
For numbers ending in 0.
If the number ends in 0, multiply it as easily as a single digit. Just add a couple of zeros.
The table is marked in red.
')
For numbers ending in 5.
To square a two-digit number ending in 5, multiply the first digit (x) by (x + 1) and add to the result “25”.
The table is marked in green.
For numbers from 40 to 50.
Hard enough, right? Let's take an example:
The table is marked with light orange.
For numbers from 50 to 60.
It is also quite difficult for perception. Let's take an example:
The table is marked dark orange.
For numbers from 90 to 100.
Similar to rule 3, but with different coefficients. Let's take an example:
The table is marked dark dark orange.
It is necessary to remember the squares of numbers up to 40. It sounds crazy and difficult, but in fact up to 20, most people know squares. 25, 30, 35 and 40 are amenable to formulas. And only 16 pairs of numbers remain. They can already be memorized using mnemonics (which I also want to talk about later) or by any other means. Like multiplication table :)
The table is marked in blue.
You can memorize all the rules, or you can memorize selectively, in any case, all the numbers from 1 to 100 obey two formulas. The rules will help, without using these formulas, to quickly calculate more than 70% of the options. These two formulas are:
For numbers from 25 to 50
For example:
For numbers from 50 to 100
For example:
Of course, you shouldn't forget about the usual formula for decomposition of the square of a sum (a special case of the Newton binomial ):
UPDATE
The products of numbers close to 100, and, in particular, their squares, can also be calculated according to the principle of “disadvantages up to 100”:
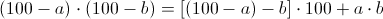
In words: from the first number we subtract the “flaw” of the second to the hundred and assign the two-digit product of the “flaws”.
For squares, respectively, even easier.
(from sielover )
Squaring may not be the most useful thing in the household. Do not immediately remember the case when you may need a square number. But the ability to quickly operate with numbers, apply the appropriate rules for each of the numbers perfectly develops the memory and "computational abilities" of your brain.
By the way, I think all readers of the habr know that 64 ^ 2 = 4096, and 32 ^ 2 = 1024.
Many squares of numbers are remembered at the associative level. For example, I easily remembered 88 ^ 2 = 7744, because of the same numbers. Everyone will certainly have their own characteristics.
I first found two unique formulas in the book “13 steps to mentalism”, which has little to do with mathematics. The fact is that earlier (perhaps now), unique computational abilities were one of the numbers in stage magic: the conjurer told the bike about how he got superpowers and, in proof of this, he instantly raises numbers to a hundred in a square. The book also indicates the methods of cube construction, the methods of subtracting roots and cubic roots.
If the topic of fast counting is interesting - I will write more.
Comments on errors and edits please write in HP, thanks in advance.

* squares to hundreds
In order to thoughtlessly not square all the numbers using a formula, you need to maximally simplify your task with the following rules.
Rule 1 (cuts off 10 numbers)
For numbers ending in 0.
If the number ends in 0, multiply it as easily as a single digit. Just add a couple of zeros.
70 * 70 = 4900. The table is marked in red.
')
Rule 2 (cuts off 10 numbers)
For numbers ending in 5.
To square a two-digit number ending in 5, multiply the first digit (x) by (x + 1) and add to the result “25”.
75 * 75 = 7 * 8 = 56 … 25 = 5625. The table is marked in green.
Rule 3 (cuts 8 numbers)
For numbers from 40 to 50.
XX * XX = 1500 + 100 * + (10 - )^2 Hard enough, right? Let's take an example:
43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849. The table is marked with light orange.
Rule 4 (cuts 8 numbers)
For numbers from 50 to 60.
XX * XX = 2500 + 100 * + ( )^2 It is also quite difficult for perception. Let's take an example:
53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809. The table is marked dark orange.
Rule 5 (cuts 8 numbers)
For numbers from 90 to 100.
XX * XX = 8000+ 200 * + (10 - )^2 Similar to rule 3, but with different coefficients. Let's take an example:
93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649. The table is marked dark dark orange.
Rule number 6 (cuts 32 numbers)
It is necessary to remember the squares of numbers up to 40. It sounds crazy and difficult, but in fact up to 20, most people know squares. 25, 30, 35 and 40 are amenable to formulas. And only 16 pairs of numbers remain. They can already be memorized using mnemonics (which I also want to talk about later) or by any other means. Like multiplication table :)
The table is marked in blue.
You can memorize all the rules, or you can memorize selectively, in any case, all the numbers from 1 to 100 obey two formulas. The rules will help, without using these formulas, to quickly calculate more than 70% of the options. These two formulas are:
Formulas (24 numbers left)
For numbers from 25 to 50
XX * XX = 100(XX - 25) + (50 - XX)^2 For example:
37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369 For numbers from 50 to 100
XX * XX = 200(XX - 50) + (100 - XX)^2 For example:
67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489 Of course, you shouldn't forget about the usual formula for decomposition of the square of a sum (a special case of the Newton binomial ):
(a+b)^2 = a^2 + 2ab + b^2. 56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136. UPDATE
The products of numbers close to 100, and, in particular, their squares, can also be calculated according to the principle of “disadvantages up to 100”:
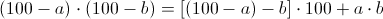
In words: from the first number we subtract the “flaw” of the second to the hundred and assign the two-digit product of the “flaws”.
For squares, respectively, even easier.
92*92 = (92-8)*100+8*8 = 8464 (from sielover )
Squaring may not be the most useful thing in the household. Do not immediately remember the case when you may need a square number. But the ability to quickly operate with numbers, apply the appropriate rules for each of the numbers perfectly develops the memory and "computational abilities" of your brain.
By the way, I think all readers of the habr know that 64 ^ 2 = 4096, and 32 ^ 2 = 1024.
Many squares of numbers are remembered at the associative level. For example, I easily remembered 88 ^ 2 = 7744, because of the same numbers. Everyone will certainly have their own characteristics.
I first found two unique formulas in the book “13 steps to mentalism”, which has little to do with mathematics. The fact is that earlier (perhaps now), unique computational abilities were one of the numbers in stage magic: the conjurer told the bike about how he got superpowers and, in proof of this, he instantly raises numbers to a hundred in a square. The book also indicates the methods of cube construction, the methods of subtracting roots and cubic roots.
If the topic of fast counting is interesting - I will write more.
Comments on errors and edits please write in HP, thanks in advance.
Source: https://habr.com/ru/post/178831/
All Articles