Chaos within us
The theory of dynamic chaos has long been a popular (one might say, "fashionable") theme among intellectuals - techies, IT people, even humanists.
Near-scientific books and Internet pages about chaos operate the same models, known almost from the 19th century: fractals, turbulence, logistic mapping ...
Meanwhile, in the last 10 years, it became clear that dynamic chaos (along with self-organization) -
the key to understanding the universe, including the origin and work of our consciousness.
Serious monographs on this topic require a high level of training and mathematical culture.
(Who has any, I recommend:
A.B. Katok, B. Hasselblat "Introduction to the modern theory of dynamical systems").
Of course, there are examples of a balanced approach:
There are also content sites:
Saratov group of nonlinear dynamics
Mysterious site
Here is a rather fresh, interesting publication about the hierarchy of chaos, stochasticity criteria.
The math there just looks scary; enough knowledge of set theory.
Here I would like to highlight a similar topic: analyze one of the criteria of chance and
suggest a home experiment for self-analysis.
There are a huge number of criteria and tests for randomness.
The aforementioned article convincingly shows that there is no binary answer to the question “chaos or not?”.
From the Lissajous figures that tightly shading the screen, to the hyper-chaos of high dimensions,
indistinguishable from throwing “honest” bones - all these systems can be evaluated using different methods
(correlations, spectrum, mixing ...), getting a hierarchy of chaos. More approaches - more faces of Chaos ...
My acquaintance with Habr, for example, began with this article
about one way to display time series. Something similar once came up with himself; I did not expect this to be such a powerful visualization method.
And yet, human consciousness tends to seek certainty, universality.
Well, let chance be a huge pagoda, from a clear sine wave to turbulence ...
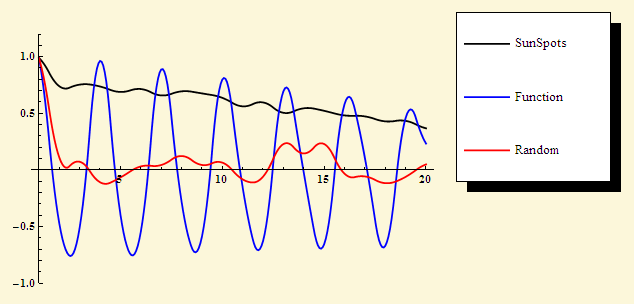
But it is so interesting (and sometimes very important) to find a universal “chaosometer”, moreover, it displays the results with an arrow, in percent. Of course, similar methods are known. The degree of attenuation of correlations, Lyapunov indicators have specific numerical values.
Autocorrelation functions for random numbers, a complex combination of sin and cos and the number of sunspots:
')
But everything is not so simple. Some methods require repeated, multiple retrieval of data series , which is not always possible. This applies to all methods that use the concept of "divergence of trajectories."
For others, an analytical model of the phenomenon is needed. For building such a model for a number of
numbers, called "simple", and you can unintentionally get a million ...
The desire to get to the bottom of the point led me in my time to the epic textbook of Donald Knut
"The Art of Programming". In Volume 2 there is a section 3.5 " What is a random sequence? ".
There, Knut analyzes the concept of ∞-distribution and writes:
This was said in 1966, but even now the “Knut method” is (imkho) the most fundamental.
I suggest everyone to re-read this chapter, the benefit of mathematics there is available literally for high school students.
Here I present some adaptation that is easy to use in practice.
1. Any data can be represented as a sequence of zeros and ones.
How to correctly bring them to this form is a separate question; in principle, the analysis of distribution can be carried out for Real, and for Integer, and even for symbols. We will work with ... 01011000111 ...
2. “Ill place” is the length of the record . Can any series of 5 zeros and units be considered random or deterministic? And out of 100? .. This leads us to the well-known paradox of "a bunch or not?"
Knut addresses this question in paragraph E.
3. Let's finally do analysis. Calculate the number of zeros and ones in the record.
Suppose that in a sequence of length N there are n zeros and Nn ones. Their relative numbers r1 = n / N,
r2 = 1 - r1 is the first characteristic of randomness. If they are very different, the data are clearly not random.
“How strong?” Is another slippery question. There is no definite answer, but you can use statistics methods.
If the shares of zeros and ones are approximately equal, then nothing definite can be said.
Indeed, in a strictly periodic series 1010101010101 ... they are also equal!
4. We divide the record into pairs . It can be different:
{abcdef ...} -> {{ab}, {cd}, {ef}, ...} or {abcdef ...} -> {{ab}, {bc}, {cd}, {de} ...}
Honestly, I did not study which way is more correct. But the overlap mode produces more pairs; use it.
From m different objects, m ^ 2 pairs can be formed. In our case, this is {00}, {01}, {10}, {11}.
We calculate their relative amount ; to the resulting set of four numbers, you can apply different statistical criteria for the degree of scatter, variance.
There is only one meaning - if there are more pairs, there is a pattern . For example, in the series 101010101 ... there are no 00 and 11 at all. The equal distribution of pairs speaks of possible chaos, but with the same proviso as before.
So "could be conceived."
5. Further steps, I think, are clear. We form triples (there will be 2 ^ 3 = 8), fours, etc.
and we will check their distribution.
According to Knut, the sequence, equally distributed for all sets, is pure, real chaos.
In practice, it makes sense to analyze sets of length no more than ld (N) (ld is the logarithm of base 2).
If they are all equally distributed, the data series is chaotic, as far as its length allows to judge.
The features of the histogram scatter for different sets can provide valuable information about the nature of the phenomenon.
Here are the histograms for the digits of the number "Pi", the residuals from dividing the prime numbers by 13 (why are they? This is a separate question) and wind directions in Moscow for 2012 (for clarity, the data were not in binary, but in decimal form)
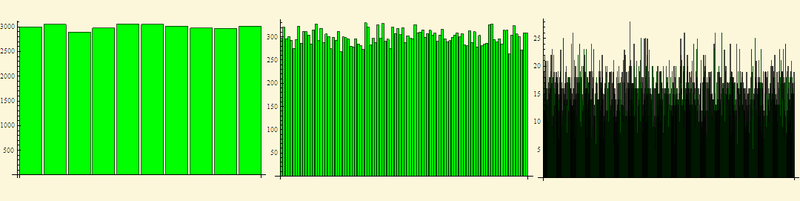
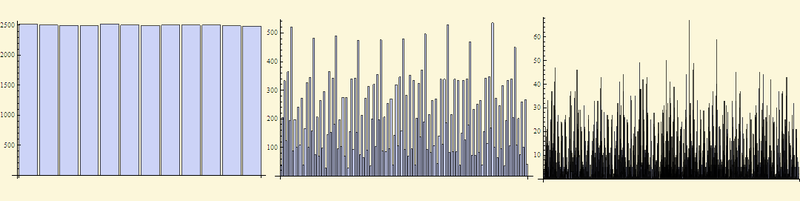
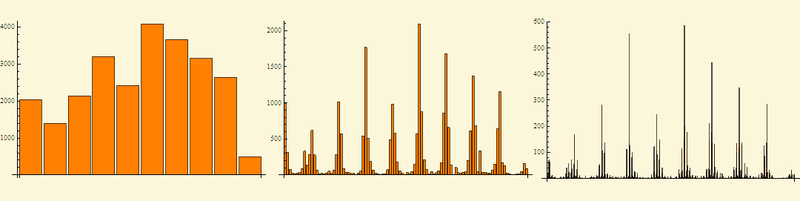
And now the promised home experiment (described in M. Schroeder, "Fractals, chaos, power laws").
Open Notepad and put the index fingers on the "0" and "1" of the keyboard.
The task is to fill a random sequence of zeros and ones.
Those who have read this article already know how we are going to assess the degree of randomness.
But believe me, it almost does not matter for further conclusions. For the purity of experience, it is of course worth
offer it to someone who is “not in the know.”
Data should be more. So it is better to close your eyes, tune in to Chaos Inside.
You can put a non-rhythmic music like dark ambient noise ...
So, the telegram is received. I think the majority of respected habrovchan will be able to write their own program
for whip analysis. On Mathematica, it takes 3 lines.
Perhaps in R there is a suitable library, although not sure.
I propose to use the applet on GeoGebra (favorite toy after Wolfram Mathematica).
Requires fresh Java plugin; may have to reload the page.
Pressing the buttons, see the analysis data of the three presets.
Copy your work, type text = "" in the applet input line and paste the data
between quotes (text = "100110101"); press Enter; characters other than 0.1 are ignored.
So, what will we see?
If you have markedly different numbers of zeros and ones, this is aclinical interest.
Perhaps you are constantly using the mouse, ignoring the hotkeys. Or shoot a lot ...
Usually they are about equal. And now couples give an amazing result.
Most "experimental" {01} and {10} are almost two times more than {00} and {11}.
With threes and fours even worse. One friend managed to fill over a thousand characters
without a single {0000} and {1111}!
For Homo Sapiens, the concept of "chaos" is consistently associated with alternation , constant switching.
Moreover, this relationship is not only on a conscious level. Try, knowing all of the above, again pobabivat random numbers. At best, it will be possible to “align” the content of pairs.
Meanwhile, True Chaos is not just a lack of order;
These are all possible types of orderliness and structures "in one bottle"!
When I mentioned the connection of our consciousness with dynamic chaos, then, of course, I did not mean its stochasticity
at all levels. You can develop the idea of the experiment - draw doodles on the tablet, make random sounds ... Analysis will show a tendency to simple “shuffle”, no more.
We cannot imitate chaos; and yet "it is somewhere nearby."
I hope to write more about this in the following posts.
Near-scientific books and Internet pages about chaos operate the same models, known almost from the 19th century: fractals, turbulence, logistic mapping ...
Meanwhile, in the last 10 years, it became clear that dynamic chaos (along with self-organization) -
the key to understanding the universe, including the origin and work of our consciousness.
Serious monographs on this topic require a high level of training and mathematical culture.
(Who has any, I recommend:
A.B. Katok, B. Hasselblat "Introduction to the modern theory of dynamical systems").
Of course, there are examples of a balanced approach:
- Gm Zaslavsky, R.M. Sagdeev "Introduction to nonlinear physics"
- S.P. Kuznetsov "Dynamic chaos"
- A. Lichtenberg, M. Lieberman “Regular and stochastic dynamics”
There are also content sites:
Saratov group of nonlinear dynamics
Mysterious site
Here is a rather fresh, interesting publication about the hierarchy of chaos, stochasticity criteria.
The math there just looks scary; enough knowledge of set theory.
Here I would like to highlight a similar topic: analyze one of the criteria of chance and
suggest a home experiment for self-analysis.
There are a huge number of criteria and tests for randomness.
The aforementioned article convincingly shows that there is no binary answer to the question “chaos or not?”.
From the Lissajous figures that tightly shading the screen, to the hyper-chaos of high dimensions,
indistinguishable from throwing “honest” bones - all these systems can be evaluated using different methods
(correlations, spectrum, mixing ...), getting a hierarchy of chaos. More approaches - more faces of Chaos ...
My acquaintance with Habr, for example, began with this article
about one way to display time series. Something similar once came up with himself; I did not expect this to be such a powerful visualization method.
And yet, human consciousness tends to seek certainty, universality.
Well, let chance be a huge pagoda, from a clear sine wave to turbulence ...
But it is so interesting (and sometimes very important) to find a universal “chaosometer”, moreover, it displays the results with an arrow, in percent. Of course, similar methods are known. The degree of attenuation of correlations, Lyapunov indicators have specific numerical values.
Autocorrelation functions for random numbers, a complex combination of sin and cos and the number of sunspots:

')
But everything is not so simple. Some methods require repeated, multiple retrieval of data series , which is not always possible. This applies to all methods that use the concept of "divergence of trajectories."
For others, an analytical model of the phenomenon is needed. For building such a model for a number of
numbers, called "simple", and you can unintentionally get a million ...
The desire to get to the bottom of the point led me in my time to the epic textbook of Donald Knut
"The Art of Programming". In Volume 2 there is a section 3.5 " What is a random sequence? ".
There, Knut analyzes the concept of ∞-distribution and writes:
"The author argues that this definition exactly meets all the reasonable philosophical requirements of randomness, and therefore, answers the basic question posed in this section."
This was said in 1966, but even now the “Knut method” is (imkho) the most fundamental.
I suggest everyone to re-read this chapter, the benefit of mathematics there is available literally for high school students.
Here I present some adaptation that is easy to use in practice.
1. Any data can be represented as a sequence of zeros and ones.
How to correctly bring them to this form is a separate question; in principle, the analysis of distribution can be carried out for Real, and for Integer, and even for symbols. We will work with ... 01011000111 ...
2. “Ill place” is the length of the record . Can any series of 5 zeros and units be considered random or deterministic? And out of 100? .. This leads us to the well-known paradox of "a bunch or not?"
Knut addresses this question in paragraph E.
3. Let's finally do analysis. Calculate the number of zeros and ones in the record.
Suppose that in a sequence of length N there are n zeros and Nn ones. Their relative numbers r1 = n / N,
r2 = 1 - r1 is the first characteristic of randomness. If they are very different, the data are clearly not random.
“How strong?” Is another slippery question. There is no definite answer, but you can use statistics methods.
If the shares of zeros and ones are approximately equal, then nothing definite can be said.
Indeed, in a strictly periodic series 1010101010101 ... they are also equal!
4. We divide the record into pairs . It can be different:
{abcdef ...} -> {{ab}, {cd}, {ef}, ...} or {abcdef ...} -> {{ab}, {bc}, {cd}, {de} ...}
Honestly, I did not study which way is more correct. But the overlap mode produces more pairs; use it.
From m different objects, m ^ 2 pairs can be formed. In our case, this is {00}, {01}, {10}, {11}.
We calculate their relative amount ; to the resulting set of four numbers, you can apply different statistical criteria for the degree of scatter, variance.
There is only one meaning - if there are more pairs, there is a pattern . For example, in the series 101010101 ... there are no 00 and 11 at all. The equal distribution of pairs speaks of possible chaos, but with the same proviso as before.
So "could be conceived."
5. Further steps, I think, are clear. We form triples (there will be 2 ^ 3 = 8), fours, etc.
and we will check their distribution.
According to Knut, the sequence, equally distributed for all sets, is pure, real chaos.
In practice, it makes sense to analyze sets of length no more than ld (N) (ld is the logarithm of base 2).
If they are all equally distributed, the data series is chaotic, as far as its length allows to judge.
The features of the histogram scatter for different sets can provide valuable information about the nature of the phenomenon.
Here are the histograms for the digits of the number "Pi", the residuals from dividing the prime numbers by 13 (why are they? This is a separate question) and wind directions in Moscow for 2012 (for clarity, the data were not in binary, but in decimal form)



And now the promised home experiment (described in M. Schroeder, "Fractals, chaos, power laws").
Open Notepad and put the index fingers on the "0" and "1" of the keyboard.
The task is to fill a random sequence of zeros and ones.
Those who have read this article already know how we are going to assess the degree of randomness.
But believe me, it almost does not matter for further conclusions. For the purity of experience, it is of course worth
offer it to someone who is “not in the know.”
Data should be more. So it is better to close your eyes, tune in to Chaos Inside.
You can put a non-rhythmic music like dark ambient noise ...
So, the telegram is received. I think the majority of respected habrovchan will be able to write their own program
for whip analysis. On Mathematica, it takes 3 lines.
Perhaps in R there is a suitable library, although not sure.
I propose to use the applet on GeoGebra (favorite toy after Wolfram Mathematica).
Requires fresh Java plugin; may have to reload the page.
Pressing the buttons, see the analysis data of the three presets.
Copy your work, type text = "" in the applet input line and paste the data
between quotes (text = "100110101"); press Enter; characters other than 0.1 are ignored.
So, what will we see?
If you have markedly different numbers of zeros and ones, this is a
Perhaps you are constantly using the mouse, ignoring the hotkeys. Or shoot a lot ...
Usually they are about equal. And now couples give an amazing result.
Most "experimental" {01} and {10} are almost two times more than {00} and {11}.
With threes and fours even worse. One friend managed to fill over a thousand characters
without a single {0000} and {1111}!
For Homo Sapiens, the concept of "chaos" is consistently associated with alternation , constant switching.
Moreover, this relationship is not only on a conscious level. Try, knowing all of the above, again pobabivat random numbers. At best, it will be possible to “align” the content of pairs.
Meanwhile, True Chaos is not just a lack of order;
These are all possible types of orderliness and structures "in one bottle"!
When I mentioned the connection of our consciousness with dynamic chaos, then, of course, I did not mean its stochasticity
at all levels. You can develop the idea of the experiment - draw doodles on the tablet, make random sounds ... Analysis will show a tendency to simple “shuffle”, no more.
We cannot imitate chaos; and yet "it is somewhere nearby."
I hope to write more about this in the following posts.
Source: https://habr.com/ru/post/178815/
All Articles