Sunday post with puzzles

Hi, Habr.
The idea is this: many of us like to break our heads in our free time. And many know a lot of interesting tasks. So why not share all this?
I, perhaps, will start with the assembly of tasks that I love, then with interviews, then from friends, then just somewhere hooked up. Please add in the comments.
')
I tried, where possible, to separate the answer and the solution. So you yourself do not inadvertently spoil the buzz from solving the problem.
Ps. Some of these tasks are VERY known, but nevertheless, the number of times that they came across to me obliges me to write them.
Drove?
Task 1: The liar paradox (where without it?). She is very simple, as many, of course, know. But a post about tasks without it would be incomplete.
Condition

You walked along the road for a long time and here you finally came to your goal. There are two doors in front of you. And you know for sure that for one treasure that you have been looking for so long, and after another a long and painful death. Two people are sitting in front of the door. You know for sure that one of them always tells the truth, and the other always lies. You also know for sure that they both know for sure which door is that. And they also know exactly who of them who. And, of course, they are both sure that you came here just for the treasure.
Question:
What one question to ask and to whom to open for sure the right door?

You walked along the road for a long time and here you finally came to your goal. There are two doors in front of you. And you know for sure that for one treasure that you have been looking for so long, and after another a long and painful death. Two people are sitting in front of the door. You know for sure that one of them always tells the truth, and the other always lies. You also know for sure that they both know for sure which door is that. And they also know exactly who of them who. And, of course, they are both sure that you came here just for the treasure.
Question:
What one question to ask and to whom to open for sure the right door?
Answer
Answer: “What door will the other of you two tell me to open?”
Decision
Decision:
Initially it is clear that there is no difference which of the two to ask. We come to anyone and ask a question from the answer. Consider two options:
- If it happened that we approached the liar, he will think that the other will say the right door and will point you to the other, as he always lies. As a result, you get the wrong door.
- if it happened that we approached the truthful person, then he will also point you to the wrong door, as he will truthfully tell you that the other will lie.
As a result, whoever we asked, we will receive an indication of the wrong door. We can only open another and enjoy the treasure.
Initially it is clear that there is no difference which of the two to ask. We come to anyone and ask a question from the answer. Consider two options:
- If it happened that we approached the liar, he will think that the other will say the right door and will point you to the other, as he always lies. As a result, you get the wrong door.
- if it happened that we approached the truthful person, then he will also point you to the wrong door, as he will truthfully tell you that the other will lie.
As a result, whoever we asked, we will receive an indication of the wrong door. We can only open another and enjoy the treasure.
Task 2: In the original “Togglers”. Let's call them "defectors". Somewhat extended problem about liars.
Condition

Before us are five people. Four of them are “defectors”. Who are these "deserters"? Everything is very simple. If any of them, regardless of the others, are asked questions, then with each next one, they will change their answers from false to true and vice versa.
We do not know in what “mood” they are initially. But we know for sure that if they once answered the truth, then the next time they lied, and vice versa - if they lied the first time, then they would surely tell the truth.
But one of these five is not a "turncoat." He always tells the truth.
Question:
How to find this fifth one, who always speaks the truth, if only two questions are possible, each of which only to one person?

Before us are five people. Four of them are “defectors”. Who are these "deserters"? Everything is very simple. If any of them, regardless of the others, are asked questions, then with each next one, they will change their answers from false to true and vice versa.
We do not know in what “mood” they are initially. But we know for sure that if they once answered the truth, then the next time they lied, and vice versa - if they lied the first time, then they would surely tell the truth.
But one of these five is not a "turncoat." He always tells the truth.
Question:
How to find this fifth one, who always speaks the truth, if only two questions are possible, each of which only to one person?
Answer
Answer:
The question can be asked, as in the previous problem, to any of them. We ask both questions to the same person.
"Do you always tell the truth?"
Farther:
- if we received the answer “Yes”, our next question will be “Who always speaks the truth?”
- if we received the answer “No”, then our next question will be “Who is a“ defector ”?”
The question can be asked, as in the previous problem, to any of them. We ask both questions to the same person.
"Do you always tell the truth?"
Farther:
- if we received the answer “Yes”, our next question will be “Who always speaks the truth?”
- if we received the answer “No”, then our next question will be “Who is a“ defector ”?”
Decision
Decision:
After the first question we can get the answers "Yes" and "No". Consider what this gives us:
- “Yes” means that either we hit the person who always tells the truth, or we hit the wrong “defector.” Thus, the next answer will be exactly true, which means if we ask "Who always tells the truth?" We will be shown the right person.
- “No” means that we hit the true “defector”. And this means that he will surely lie the next time. So our question: “Who is a“ defector ”?”, He will have to point out to us the only non-“defector” among this remarkable five.
After the first question we can get the answers "Yes" and "No". Consider what this gives us:
- “Yes” means that either we hit the person who always tells the truth, or we hit the wrong “defector.” Thus, the next answer will be exactly true, which means if we ask "Who always tells the truth?" We will be shown the right person.
- “No” means that we hit the true “defector”. And this means that he will surely lie the next time. So our question: “Who is a“ defector ”?”, He will have to point out to us the only non-“defector” among this remarkable five.
Task 3: About boxes with signs
Condition

Before us are three boxes of apples, pears, and in the third there are both apples and pears. All boxes have wonderful signs: "Apples", "Pears", "Apples and Pears".
But here's the trouble: the plates are messed up, and as it is usual, it is dark in the boxes, nothing is visible, and we can only stick our hand into the hole and get something from the box.
Question: What is the smallest amount of fruit you need to get and from where to hang the plates again correctly, if we know that the wrong plates now hang on all the boxes.

Before us are three boxes of apples, pears, and in the third there are both apples and pears. All boxes have wonderful signs: "Apples", "Pears", "Apples and Pears".
But here's the trouble: the plates are messed up, and as it is usual, it is dark in the boxes, nothing is visible, and we can only stick our hand into the hole and get something from the box.
Question: What is the smallest amount of fruit you need to get and from where to hang the plates again correctly, if we know that the wrong plates now hang on all the boxes.
Answer
Answer:
It is enough to get one fruit from the box, on which is a sign "Apples and Pears"
It is enough to get one fruit from the box, on which is a sign "Apples and Pears"
Decision
Decision:
Since we know that the tablets are wrong, there are either apples or pears in this box. Suppose we come across an apple. Then we remove the "Apples" sign from the box on which it hangs and hang it instead of the "Apples and Pears" sign. Now we have a box with the wrong “Pears” sign and we have the “Apples and Pears” sign in our hands. Now the turning point. How to figure out where to hang what? Very simple. We use the condition that we know that ALL the plates hang incorrectly, which means that we hang the “Pears” sign on the box on which “Apples” was written at the very beginning, because this sign cannot remain in its place. And we hang the sign "Apples and Pears" in the only free space.
Since we know that the tablets are wrong, there are either apples or pears in this box. Suppose we come across an apple. Then we remove the "Apples" sign from the box on which it hangs and hang it instead of the "Apples and Pears" sign. Now we have a box with the wrong “Pears” sign and we have the “Apples and Pears” sign in our hands. Now the turning point. How to figure out where to hang what? Very simple. We use the condition that we know that ALL the plates hang incorrectly, which means that we hang the “Pears” sign on the box on which “Apples” was written at the very beginning, because this sign cannot remain in its place. And we hang the sign "Apples and Pears" in the only free space.
Task 4: Pro cake and shameless bird
Condition

My grandmother had two grandsons who were supposed to come for a weekend visit. She, like any good grandmother, prepared a cake for them (very tasty). And put it on the windowsill. But while he was standing there, a shameless bird flew over the house of his grandmother. And it so happened that she settled her need right on the edge of the cake. Having seen this, the grandmother did not lose heart and decided that she would simply cut out this piece (see picture). Grandmother was very fair, loved her grandchildren equally, and treated her work tenderly. Help the grandmother to divide the rest of the cake into two parts that are exactly the same in area.
Grandmother has a perfect eye, she is easily able to find the middle and the intersection of any segments. And my grandmother has a wonderful knife (made of German steel), with which she can famously cut pieces of cake along any intended straight line.
Question:
What is the minimum number of cuts a grandmother needs to make to cut a cake?
(Specification, this is a cake, not a cake. It cannot be cut horizontally, since then one of the grandchildren will have to be content with only cream)
After cutting a piece of cake, it schematically looks like this:


My grandmother had two grandsons who were supposed to come for a weekend visit. She, like any good grandmother, prepared a cake for them (very tasty). And put it on the windowsill. But while he was standing there, a shameless bird flew over the house of his grandmother. And it so happened that she settled her need right on the edge of the cake. Having seen this, the grandmother did not lose heart and decided that she would simply cut out this piece (see picture). Grandmother was very fair, loved her grandchildren equally, and treated her work tenderly. Help the grandmother to divide the rest of the cake into two parts that are exactly the same in area.
Grandmother has a perfect eye, she is easily able to find the middle and the intersection of any segments. And my grandmother has a wonderful knife (made of German steel), with which she can famously cut pieces of cake along any intended straight line.
Question:
What is the minimum number of cuts a grandmother needs to make to cut a cake?
(Specification, this is a cake, not a cake. It cannot be cut horizontally, since then one of the grandchildren will have to be content with only cream)
After cutting a piece of cake, it schematically looks like this:

Answer

Answer 2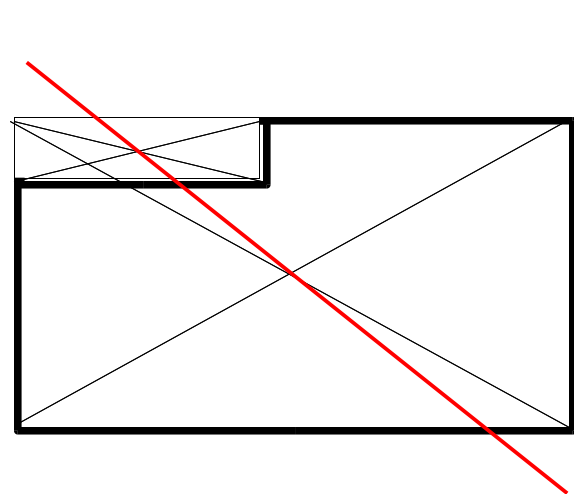

Decision
Decision:
All lines passing through the center of a rectangle divide its area exactly in half.
All lines passing through the center of a rectangle divide its area exactly in half.
Task 5: About the ladder (a more complex version of this task was already on Habré, right here )
Condition

Ten prisoners tomorrow will be put on the stairs so that everyone will look in the back to the one who stands below. This way he will see everyone who stands before him. They will wear caps on everyone. Caps will be either black or white. Of course, none of them will see the color of their cap. The caps will be distributed arbitrarily - all may be black, all may be white, and may be mixed. This will be decided by the prison wardens on the spot.
Next, the rangers go down the top of the stairs and ask everyone: "What color is your hat?". If he answers correctly, he is released into the wild. If they make mistakes, they kill.
Question:
Prisoners have a whole night to come up with a behavior strategy. Help them guaranteed to save as many people as possible.

Ten prisoners tomorrow will be put on the stairs so that everyone will look in the back to the one who stands below. This way he will see everyone who stands before him. They will wear caps on everyone. Caps will be either black or white. Of course, none of them will see the color of their cap. The caps will be distributed arbitrarily - all may be black, all may be white, and may be mixed. This will be decided by the prison wardens on the spot.
Next, the rangers go down the top of the stairs and ask everyone: "What color is your hat?". If he answers correctly, he is released into the wild. If they make mistakes, they kill.
Question:
Prisoners have a whole night to come up with a behavior strategy. Help them guaranteed to save as many people as possible.
Answer and Decision
Answer and solution:
Prisoners must choose some color. Let it be black. Then the top prisoner, number 10, should count the caps in black. Then he should say “black” if there were an even number of black caps, and “white” if there were an odd number of black caps. His life, of course, is not guaranteed. He may be lucky or not lucky.
That prisoner that is under him, number 9, should compare what he sees with what the previous one said. Let's say the first one said “black”. Further there are two options:
- Number 9 sees an even number of black caps. Then he says “white”, because the number of black caps remains the same, which means it is white. This gives number 8 the information that an even number of black caps remains.
- number 9 sees an odd number of black caps. This means that he himself is under a black hat. Then he says “black” and number 8 understands that now there are an odd number of black caps.
And so on. Thus, we guaranteed to save as many as nine prison-hardened human lives.
Prisoners must choose some color. Let it be black. Then the top prisoner, number 10, should count the caps in black. Then he should say “black” if there were an even number of black caps, and “white” if there were an odd number of black caps. His life, of course, is not guaranteed. He may be lucky or not lucky.
That prisoner that is under him, number 9, should compare what he sees with what the previous one said. Let's say the first one said “black”. Further there are two options:
- Number 9 sees an even number of black caps. Then he says “white”, because the number of black caps remains the same, which means it is white. This gives number 8 the information that an even number of black caps remains.
- number 9 sees an odd number of black caps. This means that he himself is under a black hat. Then he says “black” and number 8 understands that now there are an odd number of black caps.
And so on. Thus, we guaranteed to save as many as nine prison-hardened human lives.
Task 6: Problem about gnomes in caps:
Condition

100 dwarfs live in the cave. One day, Snow White, who, of course, lives with them, became bored and she knitted all the gnomes with colorful hats, which they gladly wear. Of course, they do not know what color the hat is wearing them, because Snow White wore them in pitch darkness.
Moreover, the gnomes are creatures rather apathetic. All they do in the cave is sit in a circle and look at each other. They do not even talk and generally do not lead any social life. Just sit, watch and think about something. Each gnome sees the other 99 dwarfs. Accordingly, everyone sees all the caps of all the dwarfs, except his own. Every day, Snow White, in order not to lose your favorite gnomes, takes them to the building in front of the cave. And each time she says to them: “Whoever in the blue cap is going to go down”. The gnomes, who are 100% sure that they are wearing a blue cap, after that will take a step forward. If the gnome believes that his hat may be of a different color, he will remain standing in his tracks. To avoid confusion, we add the fact that those gnomes who failed out were transferred to another cave. Judge that someone is missing the rest of the gnomes can only when they return to their cave and sit in their places in a circle.
Question:
What will happen on the construction, on what day and why, if we know these three things:
- Snow White, with boredom, put on all the dwarfs blue hats.
- Snow White told the gnome that there is at least one gnome in the blue cap.
- Gnomes, for many years of life in a cave, have perfected their logic to perfection. She is infallible. And each of them understands that all other gnomes have the same infallible logic.

100 dwarfs live in the cave. One day, Snow White, who, of course, lives with them, became bored and she knitted all the gnomes with colorful hats, which they gladly wear. Of course, they do not know what color the hat is wearing them, because Snow White wore them in pitch darkness.
Moreover, the gnomes are creatures rather apathetic. All they do in the cave is sit in a circle and look at each other. They do not even talk and generally do not lead any social life. Just sit, watch and think about something. Each gnome sees the other 99 dwarfs. Accordingly, everyone sees all the caps of all the dwarfs, except his own. Every day, Snow White, in order not to lose your favorite gnomes, takes them to the building in front of the cave. And each time she says to them: “Whoever in the blue cap is going to go down”. The gnomes, who are 100% sure that they are wearing a blue cap, after that will take a step forward. If the gnome believes that his hat may be of a different color, he will remain standing in his tracks. To avoid confusion, we add the fact that those gnomes who failed out were transferred to another cave. Judge that someone is missing the rest of the gnomes can only when they return to their cave and sit in their places in a circle.
Question:
What will happen on the construction, on what day and why, if we know these three things:
- Snow White, with boredom, put on all the dwarfs blue hats.
- Snow White told the gnome that there is at least one gnome in the blue cap.
- Gnomes, for many years of life in a cave, have perfected their logic to perfection. She is infallible. And each of them understands that all other gnomes have the same infallible logic.
Answer
Answer:
99 days nothing will happen, on the hundredth all the dwarfs will take a step forward.
99 days nothing will happen, on the hundredth all the dwarfs will take a step forward.
Decision
Decision:
Consider the situation not with a hundred gnomes, but something simpler, say with one gnome.
He sits in the room all day and sees no one. Since he knows that there must be at least one dwarf in a blue cap, he will make a step forward at the very first construction, since he will be 100% sure of the color of his cap.
Now consider the option when the gnome is two. They sit in a cave all day and look at each other. What do they see?
They see the opposite of a dwarf sitting in a blue cap. Now they are not sure of the color of their cap, since they know that there must be at least one gnome in a blue cap and they see it in front of them. But what would have happened if one of them saw on the other not a blue cap, but, say, a red one? This would lead him to logic from the previous step, where we had one dwarf. So he would have gone out on the first line.
When the gnomes see that this did not happen and they both remained standing as if dug in the construction (as in our case, both see the blue cap opposite themselves), each of them immediately understands, knowing that each dwarf has an infallible logic that, if another gnome would not have seen the blue cap on him, then that gnome would have gone ahead on the first line of construction. The fact that this did not happen is sufficient for both gnomes to become confident in the color of their caps and, therefore, they will come out together on the second day.
The same logic easily expands to an arbitrary number of gnomes.
Consider the situation not with a hundred gnomes, but something simpler, say with one gnome.
He sits in the room all day and sees no one. Since he knows that there must be at least one dwarf in a blue cap, he will make a step forward at the very first construction, since he will be 100% sure of the color of his cap.
Now consider the option when the gnome is two. They sit in a cave all day and look at each other. What do they see?
They see the opposite of a dwarf sitting in a blue cap. Now they are not sure of the color of their cap, since they know that there must be at least one gnome in a blue cap and they see it in front of them. But what would have happened if one of them saw on the other not a blue cap, but, say, a red one? This would lead him to logic from the previous step, where we had one dwarf. So he would have gone out on the first line.
When the gnomes see that this did not happen and they both remained standing as if dug in the construction (as in our case, both see the blue cap opposite themselves), each of them immediately understands, knowing that each dwarf has an infallible logic that, if another gnome would not have seen the blue cap on him, then that gnome would have gone ahead on the first line of construction. The fact that this did not happen is sufficient for both gnomes to become confident in the color of their caps and, therefore, they will come out together on the second day.
The same logic easily expands to an arbitrary number of gnomes.
Task 7: About two glasses:
Condition

In two identical glasses poured the same amount of different liquids. In one, wine, in the other, water (in this problem, we assume that there is no water in wine).
We collect a full teaspoon of wine from a glass, in fact, with wine and pour it into water. Carefully mix and scoop the same full teaspoon of what happened, pour it back into the wine glass.
Question:
What is more - water in wine or wine in water?

In two identical glasses poured the same amount of different liquids. In one, wine, in the other, water (in this problem, we assume that there is no water in wine).
We collect a full teaspoon of wine from a glass, in fact, with wine and pour it into water. Carefully mix and scoop the same full teaspoon of what happened, pour it back into the wine glass.
Question:
What is more - water in wine or wine in water?
Answer
Answer:
Equally
Equally
Decision
Decision:
Let in the first glass (glass 1) 8 units of wine and in the second glass (glass 2) 8 units of water. Let the spoon hold in itself 2 units of liquid. After we poured a teaspoon of wine from glass 1 into glass 2 we get:
1: 6 wine glass
Glass 2: 8 units of water + 2 units of wine
After mixing, we take a teaspoon of what came out of glass 2. In this spoon, the proportions of liquids are the same as in the glass itself. Namely:
water: 0.8 * 2 = 1.6
Wines: 0.2 * 2 = 0.4
After pouring this teaspoon back into the wine glass:
glass 1: 6.4 units of wine + 1.6 units of water
Glass 2: 6.4 units of water + 1.6 units of wine
Let in the first glass (glass 1) 8 units of wine and in the second glass (glass 2) 8 units of water. Let the spoon hold in itself 2 units of liquid. After we poured a teaspoon of wine from glass 1 into glass 2 we get:
1: 6 wine glass
Glass 2: 8 units of water + 2 units of wine
After mixing, we take a teaspoon of what came out of glass 2. In this spoon, the proportions of liquids are the same as in the glass itself. Namely:
water: 0.8 * 2 = 1.6
Wines: 0.2 * 2 = 0.4
After pouring this teaspoon back into the wine glass:
glass 1: 6.4 units of wine + 1.6 units of water
Glass 2: 6.4 units of water + 1.6 units of wine
Task 8: About a row of light bulbs. (thanks for the little nullbie )
Condition

In a row are 100 light bulbs.
Near each there is a button that switches the state of the bulb to the opposite, that is, if the bulb was turned on, then after pressing the button, it will be turned off. And vice versa.
Past the bulbs of the ranks of a hundred people. The first one presses the button of each bulb, the second one - on the button of every second one, the third one - on the button of every third one and so on.
Question:
What kind of light bulbs will burn after the passage of these 100 people, if all were initially turned off.

In a row are 100 light bulbs.
Near each there is a button that switches the state of the bulb to the opposite, that is, if the bulb was turned on, then after pressing the button, it will be turned off. And vice versa.
Past the bulbs of the ranks of a hundred people. The first one presses the button of each bulb, the second one - on the button of every second one, the third one - on the button of every third one and so on.
Question:
What kind of light bulbs will burn after the passage of these 100 people, if all were initially turned off.
Answer
Answer:
1 4 9 16 25 36 49 64 81 100
1 4 9 16 25 36 49 64 81 100
Decision
Decision:
The light is switched by those people whose sequence number is the divider of the number of the light bulb. Therefore, the light bulb will remain on if and only if there is an odd number of dividers in its serial number. Usually dividers "go" in pairs. For example, for the number 8:
8 = 1 * 8
8 = 2 * 4
That is, in this case, for the bulb with number 8 - the first person will turn it on, the second one will turn it off, the fourth person will turn it on again and the eighth one will turn it off.
The only numbers with an odd number of dividers are full squares, for example, 9:
9 = 1 * 9
9 = 3 * 3
Thus, the number 9 has 3 different dividers, which means the light bulb with this number will remain on. Similarly for all other full squares.
The light is switched by those people whose sequence number is the divider of the number of the light bulb. Therefore, the light bulb will remain on if and only if there is an odd number of dividers in its serial number. Usually dividers "go" in pairs. For example, for the number 8:
8 = 1 * 8
8 = 2 * 4
That is, in this case, for the bulb with number 8 - the first person will turn it on, the second one will turn it off, the fourth person will turn it on again and the eighth one will turn it off.
The only numbers with an odd number of dividers are full squares, for example, 9:
9 = 1 * 9
9 = 3 * 3
Thus, the number 9 has 3 different dividers, which means the light bulb with this number will remain on. Similarly for all other full squares.
Task 9: The task of the area.
Condition


Answer
Answer:
28
28
Decision
Decision:
Let's draw a straight line EF, which will be parallel to straight lines AB and CD (the point D is below, it was accidentally cut off). Now, if we move point O to point T (the intersection of the green lines), the area of the triangles will not change. Then everything is simple. If anyone comes up with another solution, I will be glad to hear it, because mine looks a bit like a crutch. I apologize for the quality of the picture, only the phone is at hand.

Let's draw a straight line EF, which will be parallel to straight lines AB and CD (the point D is below, it was accidentally cut off). Now, if we move point O to point T (the intersection of the green lines), the area of the triangles will not change. Then everything is simple. If anyone comes up with another solution, I will be glad to hear it, because mine looks a bit like a crutch. I apologize for the quality of the picture, only the phone is at hand.

Solution 2
Solution 2: Thanks for him Xitsa
Draw additional lines from point to angle. After that, the existing will become the medians of the triangles. As is known, the median divides the area of a triangle in half:
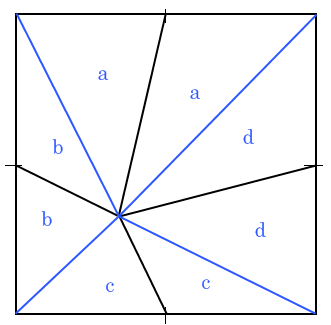
Hence the equation:
a + d = 32
a + b = 20
b + c = 16
And we easily get c + d = 32 + 16-20 = 28
Draw additional lines from point to angle. After that, the existing will become the medians of the triangles. As is known, the median divides the area of a triangle in half:

Hence the equation:
a + d = 32
a + b = 20
b + c = 16
And we easily get c + d = 32 + 16-20 = 28
Solution 3
Solution 3: Thank you for it. Oleg1977
let 2a be the side of the square; from O we omit the heights x, y, (2a-x) and (2a-y).
Further, the system of equations (squares of 4-gons from squares of 3-gons):
ax / 2 + ay / 2 = 20,
ay / 2 + a (2a-x) / 2 = 16
ax / 2 + a (2a-y) / 2 = 32
ax / 2 -a (2a-x) / 2 = 4
ay / 2 -a (2a-y) / 2 = -12
ax / 2 + ay / 2 = 20
ax = a ^ 2 + 4
ay = a ^ 2 - 12
a ^ 2 + 2 - 6 = 20
Required: a (2a-x) / 2 + a (2a-y) / 2 = 2a ^ 2 - ax / 2 - ay / 2 = a ^ 2 - 2 + 6 = 24 - 2 + 6 = 28
let 2a be the side of the square; from O we omit the heights x, y, (2a-x) and (2a-y).
Further, the system of equations (squares of 4-gons from squares of 3-gons):
ax / 2 + ay / 2 = 20,
ay / 2 + a (2a-x) / 2 = 16
ax / 2 + a (2a-y) / 2 = 32
ax / 2 -a (2a-x) / 2 = 4
ay / 2 -a (2a-y) / 2 = -12
ax / 2 + ay / 2 = 20
ax = a ^ 2 + 4
ay = a ^ 2 - 12
a ^ 2 + 2 - 6 = 20
Required: a (2a-x) / 2 + a (2a-y) / 2 = 2a ^ 2 - ax / 2 - ay / 2 = a ^ 2 - 2 + 6 = 24 - 2 + 6 = 28
Task 10: Prisoners and a light bulb
Condition

In prison are 100 prisoners. The guards wanted, as always, to have fun and they came up with the next “game”. Prisoners gather in random order with an arbitrary frequency to the room, where there is only a light bulb and a switch to it. The guards also select one of the prisoners (the responsible prisoner), who every time they come to the cell with a light bulb is asked whether all of these 100 prisoners have been in the cell. He can say that he is not sure how many times. But, if he says that, they say, yes, everyone has been, then the following happens. If he was not mistaken - they let everyone go, and if he was wrong, then, as usual, they are executed.
Question:
Prisoners have a night to come up with a cunning plan for how to be saved. Help them with developing their strategy. Initially the light is off.

In prison are 100 prisoners. The guards wanted, as always, to have fun and they came up with the next “game”. Prisoners gather in random order with an arbitrary frequency to the room, where there is only a light bulb and a switch to it. The guards also select one of the prisoners (the responsible prisoner), who every time they come to the cell with a light bulb is asked whether all of these 100 prisoners have been in the cell. He can say that he is not sure how many times. But, if he says that, they say, yes, everyone has been, then the following happens. If he was not mistaken - they let everyone go, and if he was wrong, then, as usual, they are executed.
Question:
Prisoners have a night to come up with a cunning plan for how to be saved. Help them with developing their strategy. Initially the light is off.
Answer and Decision
Answer and solution:
Prisoners must agree that the one chosen to be responsible for all should always turn on the light when it comes into the room with it. All the rest should turn it off, but touch it only once. That is, if a prisoner turned off the light one time, then he does not touch it anymore, in whatever condition it finds when he enters the room. The responsible prisoner must count the number of times he had to turn on the light bulb. As soon as he got 100, he can say with confidence that all the prisoners were in the room.
Prisoners must agree that the one chosen to be responsible for all should always turn on the light when it comes into the room with it. All the rest should turn it off, but touch it only once. That is, if a prisoner turned off the light one time, then he does not touch it anymore, in whatever condition it finds when he enters the room. The responsible prisoner must count the number of times he had to turn on the light bulb. As soon as he got 100, he can say with confidence that all the prisoners were in the room.
Task 11: A problem about a magician and a map. (I don’t remember where I took it, but I decided when I was in the queue for 4 hours for a new birth certificate. I did not decide :) ( UPD : The task caused a big stir, added clarifications in the condition and a new solution for the condition that was originally)
Condition

The magician takes a standard deck of 52 cards, and gives it to the audience. Viewers choose (in whatever way) any 5 cards and give them to the assistant magician. He looks at the cards and calls the magician 4 of them. In response, the magician calls the fifth. In addition to the card suits and meanings, the magician does not receive any additional information (the helper speaks in a steady voice, without pauses, etc.) ( Clarification: it was understood that the helper does not tell the magician anything other than the suit and name of the cards) .
Question:
How does a magician manage to "guess" the fifth card?

The magician takes a standard deck of 52 cards, and gives it to the audience. Viewers choose (in whatever way) any 5 cards and give them to the assistant magician. He looks at the cards and calls the magician 4 of them. In response, the magician calls the fifth. In addition to the card suits and meanings, the magician does not receive any additional information (the helper speaks in a steady voice, without pauses, etc.) ( Clarification: it was understood that the helper does not tell the magician anything other than the suit and name of the cards) .
Question:
How does a magician manage to "guess" the fifth card?
Answer and Decision
Answer and solution for option with clarification:
The assistant received 5 cards from the audience. Since there are only 4 card suits, then at least 2 cards have the same suit. This suit will guess the magician. The first card that the assistant will call will have the same suit as the card that the magician will have to guess (assistant in the right to choose which card not to call). With the suit figured out. To find out the type of card, the famous binary calculus system works. Since there are only 13 different cards in the deck, and the helper will call 4 cards with 4 cards being 4 bits, using 4 bits you can draw the maximum number 1111, which is 1 * 2 ^ 3 + 1 * 2 ^ 2 + 1 in the decimal system * 2 ^ 1 + 1 * 2 ^ 0 = 1 * 8 + 1 * 4 + 1 * 2 + 1 = 8 + 4 + 2 + 1 = 15, which is quite enough for the image of 13 maps. Let 2 = 2,3 = 3,4 = 4 ... 10 = 10, Jack = 11, Queen = 12, King = 13, Ace = 14. Now, to designate “1”, the card is called “first suit, then the card itself”, to indicate “0” - “first card and then suit”.
The assistant received 5 cards from the audience. Since there are only 4 card suits, then at least 2 cards have the same suit. This suit will guess the magician. The first card that the assistant will call will have the same suit as the card that the magician will have to guess (assistant in the right to choose which card not to call). With the suit figured out. To find out the type of card, the famous binary calculus system works. Since there are only 13 different cards in the deck, and the helper will call 4 cards with 4 cards being 4 bits, using 4 bits you can draw the maximum number 1111, which is 1 * 2 ^ 3 + 1 * 2 ^ 2 + 1 in the decimal system * 2 ^ 1 + 1 * 2 ^ 0 = 1 * 8 + 1 * 4 + 1 * 2 + 1 = 8 + 4 + 2 + 1 = 15, which is quite enough for the image of 13 maps. Let 2 = 2,3 = 3,4 = 4 ... 10 = 10, Jack = 11, Queen = 12, King = 13, Ace = 14. Now, to designate “1”, the card is called “first suit, then the card itself”, to indicate “0” - “first card and then suit”.
Answer and Decision
The answer and solution for the option without specifying:
First choose two cards of the same suit. Let their values x and y (modulo 13). Calculate the difference xy. If (xy + 13)% 13> 6, then put the map x, otherwise put y. Let's call the second of these cards. It determines the suit of the hidden map and the range of 6 options of values. So, if we called Volta peak, then the hidden card can only be a queen, king, ace, two, three or four of spades.
There are three cards left that need to be coded with one of 6 options. We agree in advance about any function of comparing cards in the deck, after which 6 options are coded by the order in which we call these three cards. If the remaining cards are A, B, C, where A <B <C, then hearing the sequence X, A, B, C, the magician will call X + 1, hear X, A, C, B - X + 2, ..., and X, C, B, A will say X + 6.
First choose two cards of the same suit. Let their values x and y (modulo 13). Calculate the difference xy. If (xy + 13)% 13> 6, then put the map x, otherwise put y. Let's call the second of these cards. It determines the suit of the hidden map and the range of 6 options of values. So, if we called Volta peak, then the hidden card can only be a queen, king, ace, two, three or four of spades.
There are three cards left that need to be coded with one of 6 options. We agree in advance about any function of comparing cards in the deck, after which 6 options are coded by the order in which we call these three cards. If the remaining cards are A, B, C, where A <B <C, then hearing the sequence X, A, B, C, the magician will call X + 1, hear X, A, C, B - X + 2, ..., and X, C, B, A will say X + 6.
And finally, for the mood,
Task 12: About looking cow (children)
Condition
Meet this cow. She is looking.

Question:
How, shifting 2 matches, you can make a cow look the other way?

Question:
How, shifting 2 matches, you can make a cow look the other way?
Answer and Decision
Answer:


Thank you very much for your attention! I hope you will see here something new for yourself. Write your tasks in the comments, as well as the request to indicate any inaccuracies in the drug. I am writing at night, but I hope that I have not been much wrong.
Source: https://habr.com/ru/post/178777/
All Articles