Prisoners dilemma: you are (not) alone

Recently I read a post about a prisoner dilemma that interested the community.
In this post I want to show a look at this problem from the side of game theory, based on the experience gained after studying in online courses at AI University in Berkeley. After applying this unit, the problem becomes clear and solvable.

If you build a decision tree, you get the following scheme:

where I and HE are prisoners
red lines mean testifying against another prisoner
green lines silence
A, B, C, D - four possible outcomes
A - both testify
B - I give evidence, he is silent
C - I am silent, he gives evidence
D - we are both silent

Now let's set the winnings function:
For me, the function will be f1 = -m
For it will be equal to f2 = -n

where m and n are the number of years of imprisonment obtained, mine and his respectively, the functions are taken with negation, since we want to sit behind bars less
here m and n are not dependent variables, since we have a game with a non-zero sum, otherwise the functions would look like this:
For me, f1 = -m
For him, f2 = m
here the second prisoner seeks to sit longer and tries to minimize m.
')
Take for example the data from the wiki about possible outcomes, then:
A = -2; - 2
B = 0; - 10
C = -10; 0
D = -1; -one
where the first and second number, my win and his respectively
We obtain the following scheme, which we need to solve:


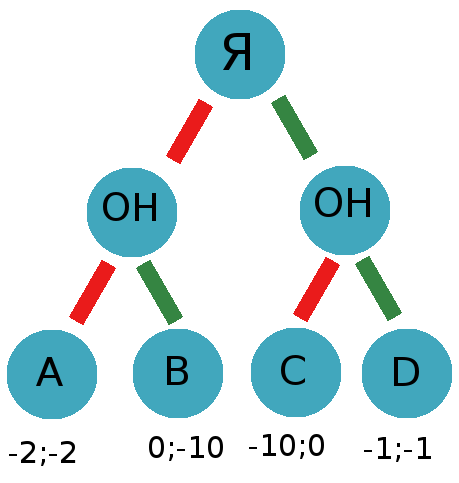
Now we will try to solve this problem and decide what course we should take. First, let's try the minimax algorithm, which in our case will be in the form of maximax, since both players try to maximize their winnings. We get the following result:

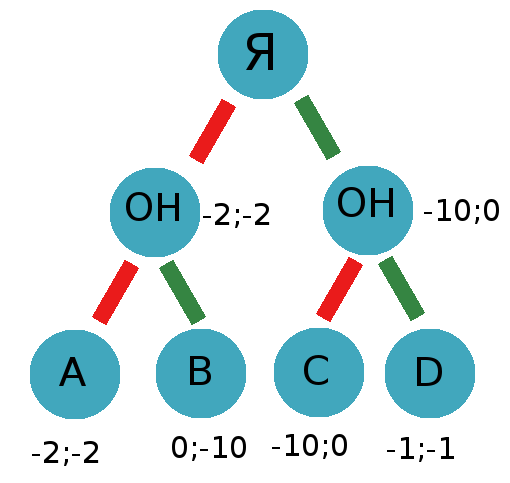
As we see, the second player will always betray, as he tries to maximize his winnings. I must also choose betrayal - based on the same reason.


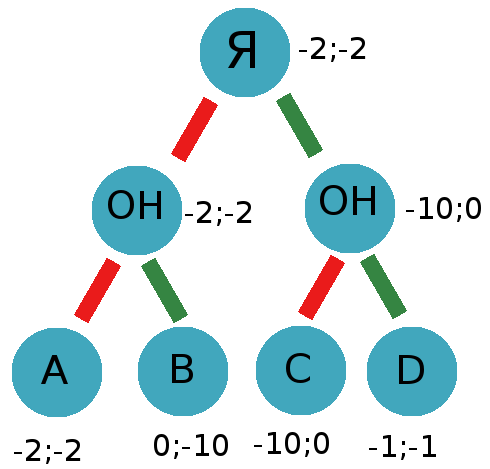
This maximax algorithm does not work well in the real world, as it is always set for a bad outcome. In such situations, the expected maximum algorithm (expectimax) shows itself significantly better. This algorithm takes into account that players can choose not the most profitable moves for themselves.
Suppose that he betrays in 50% of cases, then:
the gain of our treachery will be equal 0.5 * (- 2) + 0.5 * (0) = -1
winning our silence 0.5 * (- 10) + 0.5 * (- 1) = -5.5
or the same on the diagram:


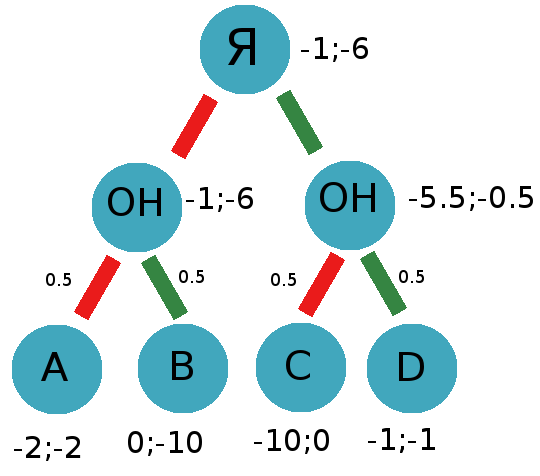
As you can see, even with a more suitable algorithm, the miracle did not happen and it is still more profitable for us to betray. Even if the probability of HIS silence increases anyway, under these conditions it is more profitable to betray. If we know that he will always be silent, we will choose betrayal.

Why is that? Where are we miscalculated?
We forgot to consider one very important detail - the winnings function. But what if we are not indifferent to HIS destiny, but he is not indifferent to OUR? Then the winnings functions will be as follows:
f1 = -m -n
f2 = -m -n
where m and n are the number of years of imprisonment, mine and his respectively
Then we get the following scheme, but this will no longer be a classical task, since one of the conditions will not be fulfilled:

and now everything changes dramatically, for maximus, the solution for ME will be silent, since I will choose between -4; -4 left (treason) and -2; -2 right (silence)
and for the expected maximum with 50% of its treachery it will turn out:
for my betrayal win -7
for my silence win -6
Therefore - silent.
Attentive habrayuzer will notice that if the probability of HIS betrayal will increase, then it will be more profitable for me to betray.

How to learn these probabilities? They can be found on the basis of previous experience.
Suppose HE earlier in 9 cases out of 10 was silent, hence we put him the probability of betrayal of 10%
True in the real world, these probabilities depend on a large number of factors and to find them is one of the main problems.

It is also worth remembering that the functions of winnings may have a different look, more selfish for ME, for example:
f1 = -m / 2 - n
here we remember about HIM, but still, if there is a choice between HIM sitting for 2 years or ME 1, I would prefer the second option.
This feature is also hard to find.

Conclusion:

This unit allows you to evaluate, present and resolve any such situation; you only need to substitute the input data.

I believe that the prisoners dilemma is a dilemma of insufficient input data. If we know with what probability HE will betray, how WE are selfish and how selfish HE will be, we will be able to make a decision very close to the right one.