Cutting into two equal parts, part one
The tasks for cutting are that area of mathematics where, as they say, the mammoth did not roll. Many individual problems, but in fact there is no general theory. Besides the well-known Bolyai-Gervin theorem , there are practically no other fundamental results in this area. Uncertainty is the eternal companion of cutting tasks. We can, for example, cut a regular pentagon into six parts, from which a square can be folded; however, we cannot prove that five parts would not be enough for this.
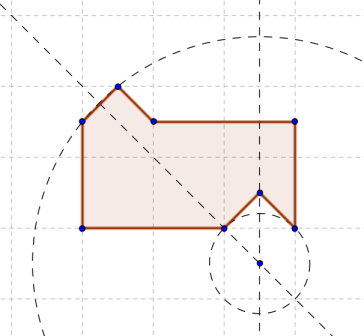
With the help of cunning heuristics, imagination and half a liter, we sometimes manage to find a concrete solution, but, as a rule, we do not have the appropriate tools to prove the minimality of this solution or its non-existence (the latter, of course, refers to the case when we have not found a solution) . This is sad and unfair. And once I took a clean notebook and decided to restore justice on the scale of one specific task: cutting a flat figure into two equal (congruent) parts. As part of this series of articles (there will be three of them, by the way), comrades, we’ll look at this funny polygon shown below and try to figure out if it’s possible to cut it into two equal shapes, or not.
')
To begin with, let's refresh the geometry school course and recall what equal figures are. Yandex helpfully prompts:
Now let's ask Wikipedia about the movement. She will tell us, firstly, that movement is a transformation of a plane that maintains the distance between points. Secondly, there is even a classification of movements on the plane. They all belong to one of the following three types:
We introduce some notation. The cut figure we will call the figure A, and the two hypothetical equal figures into which we can cut it, we call it B and C, respectively. The part of the plane not occupied by the figure A, we will call the domain D. In those cases when the particular polygon from the image is considered as the cut figure, we will call it A 0 .
So, if figure A can be cut into two equal parts B and C, then there is a movement that translates B into C. This movement can be either parallel translation, or rotation, or gliding symmetry (from this point on, I no longer stipulate that mirror symmetry is also considered sliding). Our solution will be based on this simple and, I would even say obvious, basis. In this part, we consider the simplest case - parallel transfer. Rotation and sliding symmetry fall into the second and third parts, respectively.
Parallel transfer is defined by a single parameter - the vector on which the shift occurs. We introduce a few more terms. A straight line parallel to the shift vector and containing at least one point of the figure A will be called a secant . The intersection of the secant line and the figure A will be called the section . The second section, with respect to which the figure A (minus the section) lies entirely in the same half-plane, will be called the boundary .
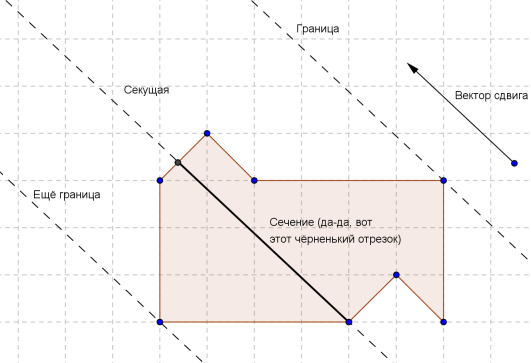
Lemma 1. A boundary section must contain more than one point.
Guided by this simple lemma, it is easy to understand that the desired parallel transfer can occur only along the vertical axis (in the current orientation of the picture) If it were in any other direction, at least one of the boundary sections would consist of a single point. This can be understood by mentally rotating the shift vector and looking at what happens to the boundaries. To exclude the case of vertical parallel translation, we need a more cunning tool.
Lemma 2. The inverse image of a point located on the boundary of a figure C is located either on the boundary of figures B and C, or on the boundary of a figure B and region D.
Theorem 1. If the section of figure A is a segment, then its length is a multiple of the length of the shift vector.
Corollary to Theorem 1. Any two sections that are segments must be commensurate.
Using this corollary, it is easy to show that the vertical parallel transport also disappears.

Indeed, the cross-section once has a length of three cells, and the cross-section two - three minus the root of two in half. Obviously, these values are incommensurable.
If the figure is A 0 and can be cut into two equal figures B and C, then B is not translated into C by parallel translation. To be continued.
With the help of cunning heuristics, imagination and half a liter, we sometimes manage to find a concrete solution, but, as a rule, we do not have the appropriate tools to prove the minimality of this solution or its non-existence (the latter, of course, refers to the case when we have not found a solution) . This is sad and unfair. And once I took a clean notebook and decided to restore justice on the scale of one specific task: cutting a flat figure into two equal (congruent) parts. As part of this series of articles (there will be three of them, by the way), comrades, we’ll look at this funny polygon shown below and try to figure out if it’s possible to cut it into two equal shapes, or not.

')
Introduction
To begin with, let's refresh the geometry school course and recall what equal figures are. Yandex helpfully prompts:
Two figures on the plane are called equal if there is a movement that is bijectively converting one figure to another.
Now let's ask Wikipedia about the movement. She will tell us, firstly, that movement is a transformation of a plane that maintains the distance between points. Secondly, there is even a classification of movements on the plane. They all belong to one of the following three types:
- Parallel transfer
- Turn
- Sliding symmetry (here I am comfortable for the sake of and benefit for including mirror symmetry , as a degenerate case, where a parallel transfer is made to the zero vector)
We introduce some notation. The cut figure we will call the figure A, and the two hypothetical equal figures into which we can cut it, we call it B and C, respectively. The part of the plane not occupied by the figure A, we will call the domain D. In those cases when the particular polygon from the image is considered as the cut figure, we will call it A 0 .
So, if figure A can be cut into two equal parts B and C, then there is a movement that translates B into C. This movement can be either parallel translation, or rotation, or gliding symmetry (from this point on, I no longer stipulate that mirror symmetry is also considered sliding). Our solution will be based on this simple and, I would even say obvious, basis. In this part, we consider the simplest case - parallel transfer. Rotation and sliding symmetry fall into the second and third parts, respectively.
Case 1: Parallel Carry
Parallel transfer is defined by a single parameter - the vector on which the shift occurs. We introduce a few more terms. A straight line parallel to the shift vector and containing at least one point of the figure A will be called a secant . The intersection of the secant line and the figure A will be called the section . The second section, with respect to which the figure A (minus the section) lies entirely in the same half-plane, will be called the boundary .

Lemma 1. A boundary section must contain more than one point.
Proof: obvious. Well, or more deployed: prove by contradiction. If this point belongs to the figure B, then its image (i.e. the point to which it will transition with parallel transfer) belongs to the figure C => the image belongs to the figure A => the image belongs to the section. Contradiction. If this point belongs to the figure C, then its preimage (the point which, if parallelly transferred, goes into it) belongs to the figure B, and then similarly. It turns out that there must be at least two points in the section.
Guided by this simple lemma, it is easy to understand that the desired parallel transfer can occur only along the vertical axis (in the current orientation of the picture) If it were in any other direction, at least one of the boundary sections would consist of a single point. This can be understood by mentally rotating the shift vector and looking at what happens to the boundaries. To exclude the case of vertical parallel translation, we need a more cunning tool.
Lemma 2. The inverse image of a point located on the boundary of a figure C is located either on the boundary of figures B and C, or on the boundary of a figure B and region D.
Proof: not obvious, but now we fix it. Let me remind you that the boundary point of a figure is such a point that, arbitrarily close to it, there are points that belong to the figure, as well as points that do not belong to it. Accordingly, near the boundary point (let's call it O ') of C, there are both points of C, as well as other points belonging either to B, or areas D. Only the points of B can be prototypes of points of C, therefore arbitrarily close to the preimage of the point O '(it would be logical to call it a point O) there are points of figure B. Any points that do not belong to B (that is, either points of figure C or points of area D) can be preimages of points of figure B. Similarly, for points of domain D. Therefore, arbitrarily close to point O, there are either points of C (and then O is on the border of B and C), or points of D (and then the preimage of B and D). If you can get through all these letters, then you will agree that the lemma is proved.
Theorem 1. If the section of figure A is a segment, then its length is a multiple of the length of the shift vector.
Proof: consider the “far” end of this segment (ie, the end whose prototype also belongs to the segment). This end obviously belongs to C and is its boundary point. Consequently, its prototype (incidentally, also lying on the segment and separated from the image by the length of the shift vector) will be either on the border of B and C, or on the border of B and D. If it is on the border of B and C, then we also take its prototype . We will repeat this operation until the next preimage ceases to be on the border C and will not be on the border D - and this will happen at the other end of the section. As a result, we obtain a chain of preimages that break the section into a number of small segments, the length of each of which is equal to the length of the shift vector. Consequently, the length of the cross section is a multiple of the length of the shear vector
Corollary to Theorem 1. Any two sections that are segments must be commensurate.
Using this corollary, it is easy to show that the vertical parallel transport also disappears.

Indeed, the cross-section once has a length of three cells, and the cross-section two - three minus the root of two in half. Obviously, these values are incommensurable.
Conclusion
If the figure is A 0 and can be cut into two equal figures B and C, then B is not translated into C by parallel translation. To be continued.
Source: https://habr.com/ru/post/178341/
All Articles