Arduino Artificial Intelligence

Currently, in the Russian segment of the Internet, the current state of affairs with the use of artificial intelligence (AI) in robotics is insufficiently covered. The desire to rectify this situation prompted to publish material related to the development technologies of intelligent control systems. The paper discusses the historical development of artificial intelligence (fuzzy logic (NL), genetic algorithms (GA), fuzzy neural networks (NNS)) for designing an automatic control system (ACS). A comparison of design methodologies is carried out on the example of a robot based on the Arduino platform.

Introduction

Currently, the development, development and implementation of effective high-tech information technologies (IT) (created in various fields of science and technology) is inextricably linked with the need to develop and improve the level of intelligence of the processes and control systems that objectively take into account controllable physical effects in the control laws , restrictions and informational boundaries that actually exist in specific models of the control object (OU).

In theory and design of control systems, at present, great attention is paid to identifying the role and effective application of robust intelligent control systems (MIS) in the intensive development and qualitative improvement of modern high-tech intellectual control of complex physical OS.
')
The complexity of the description of physical systems, in turn, leads to the need for approximation of OS models and the use of approximate solutions that do not guarantee necessary and sufficient conditions for achieving the goal of control in unforeseen situations and information risk. Therefore, in theory and control systems, one of the effective approaches to reducing the risk of decision making (from the incompleteness of the description of the OS model) is the development of robust MIS structures [1].

Evolution of intelligent control systems

The control tasks for essentially nonlinear and globally unstable OU were investigated in the presence of various types of stochastic perturbations at OU. With the help of the developed system of stochastic modeling, the limits of the classical ACS based on the use of the ACS actuator in the form of a traditional PID controller were determined (see Table 1, position 1). As a result of the study, the following fact was established: classical ACS based on a PID controller with constant gain factors often fail to cope with the control task in the case of globally unstable and substantially nonlinear op amps affected by non-Gaussian (for example, Rayleigh) stochastic noise, and also in terms of time delays in the measurement channels.

This fact is explained by the following circumstances. Classical SAUs are based on the principle of global negative feedback and the method of compensation for control error. However, in complex OU (the example with the Arduino-robot below) it is not enough to have the result of optimization only for one control quality criterion, such as the minimum of control error. Therefore, in practice, when designing MISs with complex EAs, the following problem arises: how to introduce other, additional control quality criteria into the control system?

Table 1. Evolution of ISU

Such criteria include, for example, the minimum entropy production at the OS, and / or the minimum entropy production in the control system itself (taking into account heat losses, loss of useful work in the object and control system), or other more complex vector control quality criteria.

Note. Similar and related issues of constructing a physical control theory were considered in the works of A.A. Krasovsky, S.V. Yemelyanova, Yu.I. Samoylenko, A.G. Butkovsky, L.I. Roseonoera, R. Poplavsky, A.M. Tsirlina A.P. Fradkov and many others. other

Solving this issue through the design process of a standard PID controller with constant gains is almost impossible. The limited ability to implement complex management quality criteria in classic ACS, especially in the above management cases, served as a starting point for the development of MIS based on ideas close to the use of management strategies used by a human expert in difficult situations.

For the simulation of “man-machine” control strategies, at the first stage, so-called “soft computations” began to be used, which are based on the theory of fuzzy sets and fuzzy inference. Thus, for example, the structure presented in Table 1-1 is converted into an expert control system. Table 1-2 by successively building up the component blocks in the classical ACS structure (in this case, the introduction of a fuzzy output block) and is an example of the first generation of MIS (Fig. 1).

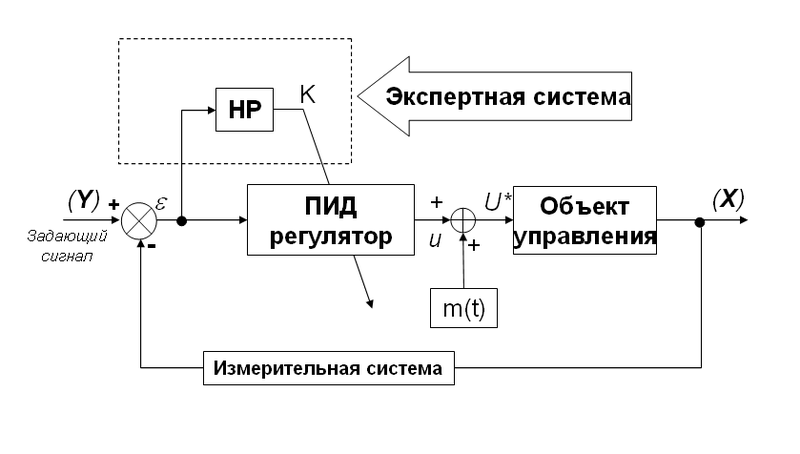
Fig. 1. Control system with a fuzzy regulator

Thus, the first generation of MIS was a fuzzy expert system (ES). The main role in these ECs was played by the quality of the knowledge base (KB), which was determined by the experience and subjective knowledge of the human expert. However, in the case of control of globally unstable and substantially non-linear OA under the influence of complex stochastic noise, even an experienced human expert finds it difficult to find the optimal (from the point of view of control quality) NRB. This problem is the bottleneck of all the first (and their subsequent modifications) MIS. Therefore, the use of ES as a tool for extracting knowledge and forming knowledge bases (as the basis of MIS design technology) did not lead to the expected significant success (although there are many examples of industrial implementation) due to the complexity of the OS and the subjectivity of the information contributed by the expert.

From the point of view of design technology, the main problem of introducing the first generation MIS was their poor adaptability to changes in the OS parameters (caused, for example, by the aging of the OS structure or a sharp change in the external environment), as well as the low robustness of the obtained control laws. To solve these problems, second generation IMSs were developed using soft computing technologies, combining GA, NNS and fuzzy controller (NR) into a single chain. This allowed us to exclude the subjective expert opinion at the stage of formation of the structure and parameters of the KB of HP. In turn, the development of MIS, based on soft computing, has given rise to several approaches to the formation of BR structures. Initially, it was planned to generate some rather coarsened training signal (OS) from the GA, and extract the BRs by approximating the resulting OS on the NNS. The structure of the second generation MIS is represented by introducing into the structure of the MIS the first generation of the block, including the GA and NNS (see, Table 1 - 3).

Subsequently, the second generation of MIS began to use a new kind of feedback, called intellectual global feedback (IGOS), presented in Table 1, (position 4). Its use makes it possible to extract objective knowledge directly from the dynamic behavior of the OS and the actuator of the ACS. The IGOS circuit includes the GA for obtaining information about the optimal control signal (based on the dynamic and thermodynamic behavior of the OS and the PID controller itself) and the NNS approximating this optimal control signal using the specified neural network structure. The main unit in the structure of the MIS of this generation is the system for simulating the optimal control signal (IMSMS) using the GA and the control quality criterion specified as one of the components of the vector fitness function of the GA (Fig. 2).

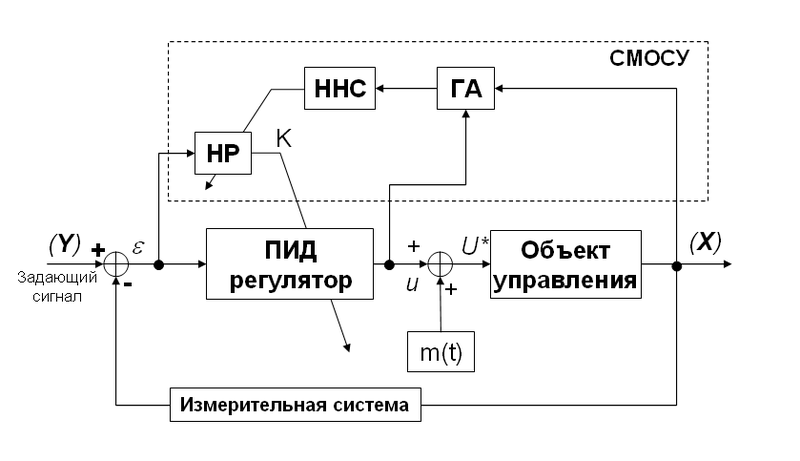
Fig. 2. Intelligent second generation control system

The main problem solved by the fifth generation MIS with IGOS is the possibility of achieving the required level of robustness in a given class of both parametric and external random disturbances of various probabilistic nature (with different functions of the probability distribution density). Another important problem is the determination of the required ratio between the accuracy of the description (approximation) of the OS and the required level of robustness of the entire HHC structure. Both of these problems are solved at the second stage of the technology of building the BZ of the MIS using the software tools of the toolkit, called the “Knowledge Base Optimizer” (OBZ) (Fig. 3).

Fig. 3. Intelligent control system of the fifth generation. With software tools OBZH

You can learn more about the method of designing MIS using examples of designing such systems:
Intelligent manipulator control
Method of extracting knowledge from a physically measured signal
Remote configuration of KB

Consider an example of the use of ISAU.

Mathematical model and Robot

The control of an object like “Carriage is an inverted pendulum” (Fig. 4) is one of the typical tasks in control theory, since The solution to this problem clearly demonstrates the quality of the ACS. Consider the model dynamics in the form of a single-axis carriage with an inverted pendulum fixed on the axis:

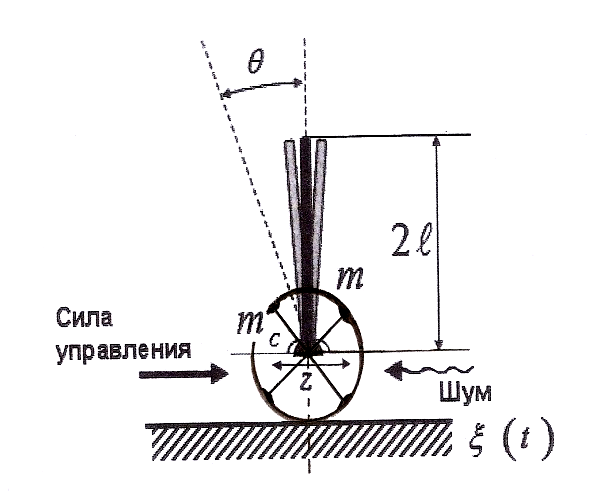
Fig.4 Model of the system "Carriage-inverted pendulum"

The dynamics of this OA is described by a system of second-order differential equations derived, taking into account the friction forces and the carriage elasticity, from the balance of moments and projections of forces on the horizontal Z axis:

The equations for the entropy production rate are as follows:

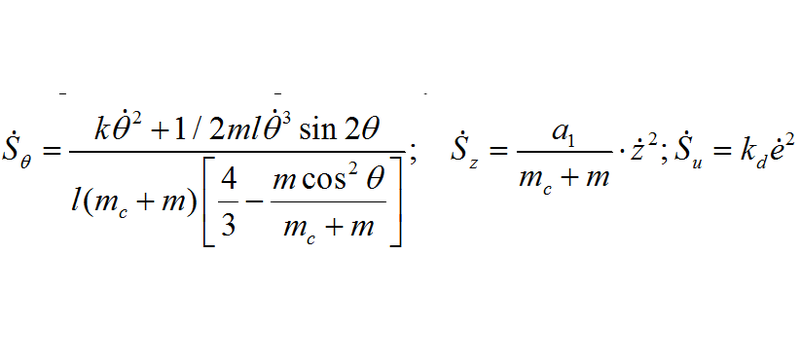
In the equations z and "theta" - the generalized coordinates; g is the acceleration of free fall, ms is the mass of the trolley, m is an inverted pendulum (called a “pole”), l is half the length of the pendulum, k and a1 are the friction coefficients in z and theta, respectively, a2 is the elastic force of the trolley, xi external stochastic noise, and u - control power.

The dynamic system has a global dynamic instability, in the absence of a control force, an unlimited increase in the deflection angle occurs, i.e. the pendulum falls. The task of controlling the system is to act (by stabilizing) the pendulum in a vertical position (the angle of deflection of the axis of the pendulum from the vertical to 0) when the operating environment changes.

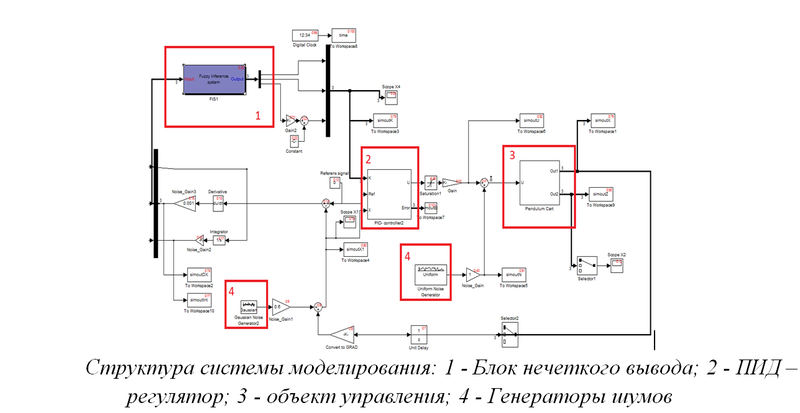
Fig.5. Mathematical model implemented in Matlab Simulink

The model (Fig. 5) includes a PID controller, noise in the control and measurement system, as well as a unit that generates a signal for the controller.
This computer model is used to receive the training signal and adjust the KB with the use of OBZ. The main stages of building a KB with the use of an OBZ are considered in [1,9].

This type of OS is typical (benchmark) for testing software tools for robust intelligent control. Examples of such systems are considered in [2 - 8] and are presented in Fig. 6

Fig. 6. Similar OU

Consider the device similar to the layout of the OS. In fig. 7 presents the layout used to test the design of ISAU using OBZ. In detail this type of robots is considered here .

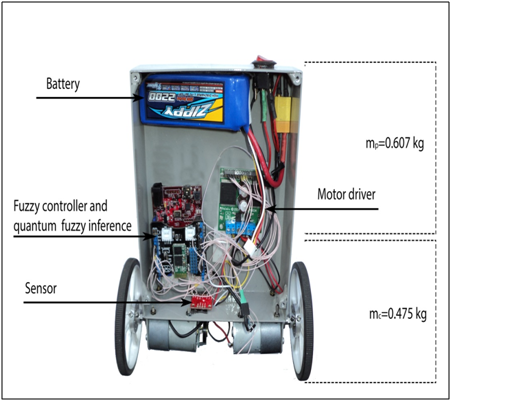
Fig. 7. Layout of the system

As a measuring system (Fig. 7, Sensor), a motherboard with a combination of sensors - a gyroscope and an accelerometer - 5 DoF (five degrees of freedom) IDG500 / ADXL335 is used in the layout. The core and central elements of the system is an Arduino microcontroller based on an ATmega328 processor. The board is equipped with a USB connector to transfer data from the processor to the computer. The USB interface is used when conducting experiments to transmit and receive data (deviation angle and magnitude of the control action), as well as for remote configuration, which will be discussed below. The sensors are connected using the analog inputs of the microcontroller.
The basic functions of the layout programs are presented in Fig. 8., generally they can be written in pseudocode:
• Measurement
• Filtering
• Management
• Counting time (delay).

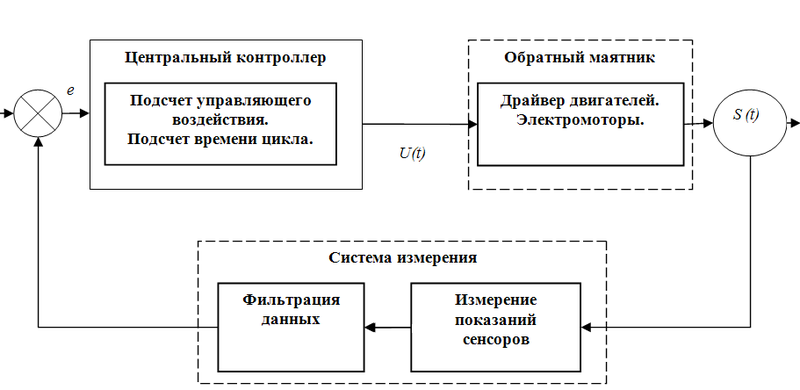
Fig. 8. Pseudocode of the robot operation algorithm

Note that the algorithm of the system layout, presented in Fig. 8 is a particular example of ACS with feedback, discussed earlier (table 1-1).

Experiment

To test the robustness of the controllers, we use two control situations:

1) Typical situation - for which to develop regulators (the situation described in the OS and mate. Models)

2) Unforeseen situation 1 - additional noise in the system (croup was used in the experiment)

3) Unforeseen situation 2 - the delay of control action is increased three times.

The video shows three types of controls:

1) Classic PID - regulator
2) Fuzzy controller based on OBZ
3) Quantum regulator based on new types of calculations using hidden quantum information (description of the quantum regulator and design technology of a similar MIS here and here ).

findings

The structure of this design technology of fuzzy regulators and MIS should include:

o multi-criteria GA for finding optimal control and verification of mathematical models,

o a fuzzy neural network for approximation of the optimal control signal found by the GA and extracting an “optimal” BR, based on it,

o “fine” tuning of the BZ based on GA using information-entropy criteria.

OBZH allows you to implement the principle of designing the optimal MIS with the maximum level of reliability and controllability of complex OU in conditions of uncertainty of the initial information.

The use of KBs, designed using OBZ, in the structure of the MIS expands the scope of industrial applications of ACS to complex dynamic OU.

Links

1. Ulyanov S.V., Litvintseva L.V., Dobrynin V.N., Mishin A.A. Intellectual robust control: soft computing technologies, Moscow: VNIIgeosystem, 2011.

2. Grasser, F., D'Arrigo, A., Colombi, S. and Rufer, A. Joe: A mobile inverted pendulum. // IEEE Transaction Electronics. - 2002. - Vol. 49. - No 1. - pp. 107 - 114.

3. Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-order disturbance observer // IEEE International Conference on Robotics and Automation Pasadena, CA, USA, May 19-23, 2008. - pp. 2521 - 2526.

4. Nawawi SW, Ahmad MH and Osman JHS, Real-time control system for two-wheeled inverted pendulum mobile - robot, // Advanced Knowledge Application in Practice / I. Fuerstner (Ed). - InTech. - 2010. - pp. 299 - 312.

5. Gocmen A. Design of two wheeled electric vehicle. - Master Sci. Thesis. - Atilim University, Temmuz. - 2011.

6. Takeneka T., Hirano M., Izumi H., Kuwabara K., Koyama K., Kobashi Sh. Inverted pendulum mobile vehicle. - Patent US 8,224,891 B2. - Date of Patent. - Jul. 24, 2012.

7. Castro A. A two-wheeled inverted pendulum modeling and dynamic analysis. - Master Science Thesis. - Georgia Institute of Technology, Atlanta, USA. - 2012.

8. Nasir, A., Ahmad, N., Ghazali, R., Pakheri, N. The PID controller for the highly nonlinear two-wheels balancing robot // 1st International Conference on Informatics and Computational Intelligence. - IEEE Computer Society. - 2011. - pp. 176 - 181.

9. Reshetnikov A.G., Ulyanov S.V., A method for extracting knowledge from a physically measurable learning signal: designing a knowledge base of a fuzzy regulator, “System analysis in science and education” El No. FS77-51141 from 14.09.2012. Issue number 1, 2013