Geekly Articles each Day
📜 ⬆️ ⬇️

Russian Code Cup 2013: analysis of the tasks of the first qualifying round


On Saturday, April 13, 2013, at 19 o'clock the first qualifying round took place. Despite the seemingly unlucky date, for many this day turned out to be, on the contrary, very successful.
In this post we will briefly describe the results of the first qualifying round and analyze in detail the tasks that we offered the participants.
In today's parse participate:

Let's start with the results. 765 people took part in the qualification (note that this is the number of participants who sent their solutions; there were a lot more registered).
Participants were given 2 hours to solve problems. The tasks themselves were published on the website directly at the beginning of the qualifying round, so none of the participants could read them beforehand - everyone was on an equal footing.
The geographical distribution of participants turned out to be truly global, although, of course, the number of Russian participants was maximum. So, in descending order:

Russia - 540
Ukraine - 81
Belarus - 46
United States - 21
Armenia - 20
Kazakhstan - 15
Uzbekistan - 6
Georgia - 6
Germany - 6
Switzerland - 5
Sweden - 2
United Kingdom - 2
Netherlands - 2
Kyrgyzstan - 2
Poland - 2
Iceland - 1
Tajikistan - 1
Ireland - 1
Japan - 1
Spain - 1
Lithuania - 1
Israel - 1
Czech Republic - 1

201 people went to the qualifying round. Below is a list of 10 participants who first went to the qualifying round:
1. Vladislav Epifanov
2. Sergey Rogulenko
3. Ivan Popelyshev (3rd place)
3. Peter Mitrichev (another third place)
5. Anton Raichuk
6. Vladislav Isenbaev winger
7. Anton Lunev
8. Egor Kulikov
8. Gennady Korotkevich
8. Roman Rizvanov
As can be seen from the list, some participants divided the seats under the same number, because they scored the same number of points.
And now we proceed to the analysis of tasks. Participants will be able to verify their decisions, and those who have not yet qualified - to practice and check their versions (by the way, the following qualifying rounds - May 11 and June 2).
')
Problem A. Olympiad
Idea: Vitaly Aksyonov
Realization: Vitaly Aksyonov
Analysis: Vitaly Aksyonov
Detailed statement of the problem
Time limit - 1 second
Memory limit - 256 megabytes
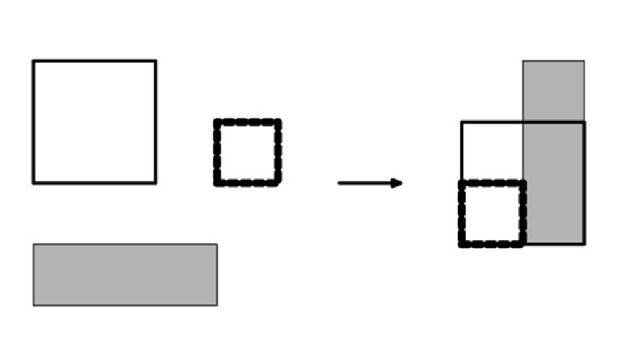
Now in Gnomlyandia is preparing for the upcoming Olympiad. The task was assigned to the gnome-brigadier - to build fields for playing hertball, jordanball and medwebol. Each field is a rectangle. In accordance with the rules of the games, the fields must be located in such a way that their sides are parallel to the north-south and west-east directions.
Land in Gnomeland is very expensive, so game organizers want to spend as little money as possible on land purchases. Since Hurtball, Jordanball and Medwebol competitions will be held at different times, the fields may overlap.
Help the dwarves find the minimum area that three fields can occupy after construction.
One of the possible optimal locations of the fields in the first example is shown in the figure.

Input Format
The input data contains no more than 1000 lines, each of which contains a description of three fields - six natural numbers, each of which does not exceed 10,000.
The first and second numbers denote the dimensions of the first field, the third and fourth - the dimensions of the second field, the fifth and sixth - the dimensions of the third field.
The input ends with a string consisting of six zeros. This request does not need to be processed.
Output format
For each set print the number - the minimum area that three fields can occupy.

In order to solve the problem, it can be noted that there is an optimal solution, in which all three given rectangles have one of the corners.
Perform a search of how to put each field - vertically or horizontally. After we have fixed the position of the fields, it is enough just to calculate the area of ​​the union of the rectangles. It can be calculated as follows: S = S 1 + S 3 + S 3 - S 12 - S 23 - S 13 + S 123 , where S i is the area of ​​the i-th rectangle, S ij is the area of ​​intersection of two rectangles with numbers i and j, and S 123 is the intersection area of ​​all three rectangles.

Problem B. Trapezoid map and trapezium
Idea: Vitaliy Demyanyuk
Realization: Vitaliy Demyanyuk
Analysis: Vitaly Demyanyuk
Detailed statement of the problem
Time limit - 2 seconds
Memory limit - 256 megabytes
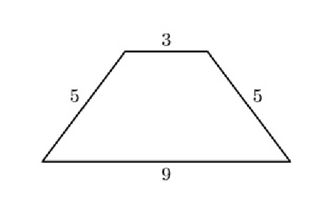
Once Anton Sergeevich told students an algorithm for constructing trapezoid maps. As a warm-up, he gave them the trapezoid problem. He drew n pieces on the board. The length of the i-th segment is equal to ai. Students need to find the number of different sets of four segments, from which you can make an isosceles trapezium of nonzero area.
Recall that an isosceles trapezium is a quadrilateral, the two opposite sides of which are parallel, and the other two are equal. An example of an isosceles trapezoid is shown in the figure.

Two sets are considered different if there exists a segment belonging to the first set and not belonging to the second. The numbers of the segments taken in each set must be pairwise different.
Help students find the number of such kits.
Input Format
The first line contains the number t - so many times Anton gave his students this task. The following 2t lines contain descriptions of all tasks.
The description of each task consists of two lines. The first line of the description gives the number n - the number of segments drawn on the board. The second line of the task description contains n integers ai - their lengths (4 ≤ n ≤ 5000, 1 ≤ ai ≤ 108 for all i from 1 to n).
The total number of all segments in all problems does not exceed 5000.
Output format
For each task in a separate line print one number - the required number of sets.

Denote the lengths of the smaller and larger parallel sides of the trapezoid by a and b, respectively, and by c, the length of the sides. Then a trapezoid can be composed only if a + 2c> b. Looking through a, b and c, we get the solution for O (n 3 ).
Note that for a fixed b and increasing c, the minimum possible a decreases. We will iterate b in the order of magnification and, with a fixed b, we iterate through c in the same order of magnification. When iterating c, we will support a pointer to the minimum possible a. Knowing b, c, the minimum possible a, and using simple combinatorial formulas, it is easy to calculate the number of sets of four segments that form a trapezoid with given parameters.
You also need to remember to handle cases in which a = b, a = c, b = c, and carefully ensure that each of the four numbers of segments are pairwise different. The total complexity is O (n 2 ).

Task C. Mluran storage
Idea: Vitaly Aksenov
Realization: Pavel Krotkov
Analysis: Pavel Krotkov
Detailed statement of the problem
Time limit - 2 seconds
Memory limit - 256 megabytes
Discovered in 2345, the chemical element mouran is very radioactive. Improper handling of the cranberry can lead to unpredictable consequences, so when using it, storing and transporting it is necessary to take extra care.
There are many different isotopes of muran, each of which is characterized by one natural number — its atomic mass. With long-term storage together of any pair of isotopes, the sum of the masses of which is equal to one of the k "critical numbers", this pair of isotopes reacts and an explosion occurs. It is known that all critical numbers are non-negative powers of two.
In the nuclear laboratory of Flatland, samples of the muran are stored in two special warehouses. Scientists managed to get n different isotopes of mluran, the masses of which are numbers from 1 to n. Now it is necessary to distribute isotopes in warehouses for storage. Such storage methods are called safe when each isotope is stored in exactly one warehouse, and any two different isotopes, the sum of the masses equal to one of the “critical numbers”, are stored in different warehouses.
Help scientists figure out how many different safe ways of storing a muran exist.
Input Format
The input to the task contains several test cases. The description of each set consists of two lines.
The first line of the description contains two integers n and k (1 ≤ n ≤ 1018, 1 ≤ k ≤ 61) - the number of isotopes that must be stored, and the number of “critical numbers”. The next line contains k different natural numbers, each of which is a power of two and does not exceed 2n - critical numbers. Critical numbers are separated from each other by spaces.
The number of data sets in each test does not exceed 10,000. The last line of the test contains two zeros.
Output format
For each test suite on a separate line, print the number of safe ways to store all isotopes in two warehouses, modulo 109 + 7.

We first implement a solution that works in linear time. We will consider the masses of isotopes in ascending order, starting with 1. Let k be the current number, and 2 t be the minimum power of two, greater than k. In this case:

Note that the answer is 2 x + d , where d is the number of powers of two, not less than 1 and not greater than n, and x is the number of such numbers that are not powers of two, that their minimum greater power of two does not lie in the set of “critical numbers ". So, you can split all the numbers from 1 to n into log 2 n segments, the boundaries of which are adjacent powers of two, then select the desired segments and sum up their lengths.

Task D. Protection of the planet
Idea: Vitaly Aksyonov
Realization: Nikolay Vedernikov
Analysis: Nikolay Vedernikov
Detailed statement of the problem
Time limit - 2 seconds
Memory limit - 256 megabytes
After the recent fall of the meteorite in the Urals, many governments have thought about protecting the Earth from asteroids. For this, the International Anti-Meteoritic Agency (MA) was created, to which the best scientists in the field of astrophysics were invited.
For several weeks, scientists have found that n asteroids fly close to the Earth, and if the asteroid is at a distance of strictly more than R from Earth, then it does not pose a danger to it. For simplicity, scientists have suggested that all asteroids near the Earth fly in a straight line, and determined their position and velocity vector at zero time. Now scientists want to learn how to respond to requests how much asteroids pose a danger to the Earth at some point in time.
For convenience, we introduce a rectangular Cartesian coordinate system. Let the Earth has coordinates (0, 0, 0). All asteroids and the Earth are considered material points in space.
Multiple queries on specific points in time. For each of them, it is required to determine how many asteroids at this moment represent a danger to the Earth.
Input Format
The first line contains two integers n and R (1 ≤ n ≤ 100000, 1 ≤ R ≤ 106) - the number of asteroids and the radius of the danger zone.
Each of the next n lines contains six integers xi, yi, zi, vxi, vyi and vzi (−106 ≤ xi, yi, zi ≤ 106, −100 ≤ vxi, vyi, vzi ≤ 100) - coordinates that specify the initial position and velocity vector of the i-th asteroid. It is guaranteed that the velocity vector is not equal to 0.
The next line contains one integer m (1 ≤ m ≤ 100000) - the number of points in time that interest scientists.
Each of the next m lines contains a single integer ti (0 ≤ ti ≤ 107) - the point in time that interests scientists.
Output format
For each time point, output a single integer - the number of asteroids that are in the danger zone.

Consider each meteorite and find the times of entry and exit into the danger zone. To do this, in the equation of the sphere x 2 + y 2 + z 2 = R 2, we substitute the equation of a straight line defining the trajectory of the meteorite, that is, x = x 0 + dx • t, ​​y = y 0 + dy • t, ​​z = z 0 + dz • t. We get a quadratic equation for time. The roots will be of interest to us at times. In this problem, problems could arise with the accuracy of floating-point numbers, so if the root of the equation was close enough to an integer, it needed to be rounded.
Add these times to the queries and sort them in ascending order. If the time is the same, then first the times that correspond to the entry time will go, then the requests, and at the end - the exit times from the danger zone. Let's get a counter that counts how many meteorites we have in the danger zone. If the current time is the entry time, then increase it; if this is a request, then we write down the answer to this request, otherwise we reduce the answer.
Operating time O ((n + m) • log (n + m))

Problem E. Teleports
Idea: Anna Malova
Realization: Boris Minaev
Analysis: Boris Minaev
Detailed statement of the problem
Time limit - 2 seconds
Memory limit - 256 megabytes
The year 2112 was coming to an end, and together with a small team of like-minded people you decided to go in search of treasures in one abandoned country. The cities of this country are connected by roads, on which you can move in both directions. You know that the people of this country loved to bury their treasures along these roads. Therefore, you want to drive through all the roads of this country and find buried treasures. You need to make an effective travel plan in advance. To do this, choose a city from which to start your journey. Further, moving along the roads, visit some more cities. A plan is called effective if each road is visited by you exactly once.
Drawing up a plan is complicated by one fact. Some pairs of cities are connected by teleports. For example, if City A and City B are connected by teleport, then, arriving along a certain road to City A, you immediately teleport to City B and can only continue on roads that are connected to City B. Similarly, if you come along the road to city ​​B, then immediately teleport to city A and continue along the roads that are connected to city A.
Each city can be connected by teleport to no more than one other city. You need to make an effective travel plan.
Input Format
The input contains descriptions of several tests. Each test has the following structure. The first line contains three integers n, m, k (1 ≤ n ≤ 105, 1 ≤ m ≤ 105, 0 ≤ k ≤ 105) - the number of cities, the number of roads and the number of teleports. The following m lines contain two different numbers - the numbers of the cities that are connected by the next road. Next, k lines contain two different numbers each, describing pairs of cities that are connected by teleports.
There can be several roads between two cities. No city is connected to itself with itself. No city is teleported to itself. Any city is connected by teleport to no more than one other city.
It is guaranteed that the total number of cities in all tests does not exceed 105. Similarly, the total number of roads and the total number of teleports also do not exceed 105. The last line of input contains three zeros. They do not need to process.
Output format
For each data set, print the answer in the following format: if an effective visit plan cannot be made, output No. in a single line. Otherwise, print Yes in the first line and m numbers denoting road numbers in the second line. Roads should be displayed in the order in which they should be visited. Roads are numbered from one in the order in which they are given in the input data. For each test, the roads are numbered independently.

For convenience, we denote the number of roads that lead to the city i, as with i . First we need to determine if there is an effective travel plan at all. First, if there are two cities i and j such that with i ≠ 0 and with j ≠ 0 and there is no path between i and j, then we cannot build a plan. It should be noted that the path may contain not only roads, but also teleports.
Suppose we have already built some path that goes through all the roads. It is clear that for all cities that are not connected by teleporters are not the first or last city on the way, with i must be even. If two cities i and j are connected by teleport and neither of them is the first or the last city on the way, then i must be equal to j .
Consider what happens to the cities that lie at the ends of the path. First, if the city i is connected by teleport with j and lies at the end of the path, then with i = with j + 1 (except for the case when j is also the end of the path). Moreover, if the path begins and ends in city i, then with i = c j + 2. If the city is not connected by teleport to another and is located at one of the ends of the path, then it can be odd with i .
As a result, to verify the existence of a path, you must do the following. Calculate for each city a certain value of a i . If city i is connected to j by a teleport, then a i = max (0, c i - c j ). Otherwise, a i = i mod 2. If the sum of all a i is two or zero, then the path exists, otherwise it does not.
Building a plan to visit a country is similar to building an Euler path in a regular graph. You need to start the search from the top, where a i ≠ 0; if there is no such, then from any one with i ≠ 0. When moving to the next vertex, if it is connected to another teleport vertex, you just need to go to it and continue the search further. The proof of the fact that there really is a complete path is analogous to the proof of the existence of the Euler path in an ordinary graph.
The total complexity is O (n + m + k).

All problem solutions will also be published on the official website of the Russian Code Cup . Those who read to the end and feels excitement can register for the following qualifying rounds - there is still time!

Source: https://habr.com/ru/post/177171/

More articles:


All Articles