Solving the problem of finding the angles of installation of a video camera over the road using different methods in Wolfram Mathematica. Part 2

Last time, we loaded data from a file, parsed it into a structure, got the equations of the vehicle's motion tracks, and graphically displayed this data: Part 1

In this article, using one of the methods, we find statistically a point in the vicinity of which the tracks of the vehicle's motion intersect.

Description of one of the ways to find the point of interest

In this method, we will find all the intersection points of the graphs — the tracks of the vehicle’s motion; we will find the expectation of these data and the variance.
')

Finding all the points of intersection of tracks

Determine the number of equations in the list with the equations:

length = Length[numeq];

Create an empty list in which we will write the coordinates of the points of intersection of the tracks:

rootlist = {};

Now you need to write a loop. which will solve the linear equations we have in pairs and find the coordinates of their intersection and write them in the prepared list ::

Do[Do[rootlist = Append[rootlist, List[
x /. Solve[numeq[[j]] == numeq[[i]], x][[1]],
numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]
]
]
, {i, 1 + j, length}],
{j, 1, length}]

On each pass of the cycle, we add to the rootlist list consisting of the x and y coordinates of the intersection of the j and i equations, with the x coordinate being:

x /. Solve[numeq[[j]] == numeq[[i]], x][[1]]

, wherein

Solve[numeq[[j]] == numeq[[i]], x]

returns a list of the roots of this equation:

{{x -> 2586.14}}

, and our record selects the first root, it is the only one here, and performs substitution, i.e. instead of x before the operator /. its value x -> 2586.14 substituted x -> 2586.14 .

expr /. x > value expr /. x > value - in the expression expr instead of the variable x it is substituted
value value.

Thus, the X coordinate of the intersection of two tracks is found, a similar action is performed to find the Y coordinate, only the root value is now substituted into one of the equations, in this case, j, and it can also be an equation with i:

numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]

Next, round up the value of our points to the whole:

rootlist = Round[rootlist];

Now we have a list of points of intersection of tracks and can begin to aggregate.

The list looks like this:

{{2586, -910}, {2716, -1014}, {2718, -1015}, {3566, -1697}, {2697, -999}, {2957, -1207}, ... }

Statistical processing of results

We define a mat waiting for the X coordinate of the intersection list:

Xmed = Mean[rootlist[[All, 1]]] // N
2532.7

Mean[data] - returns the average data value of data.

N[expr, n] - returns the result of the calculation of the expression expr up to n digits after the decimal point

x // f - Postfix form for f[x]

Define the variance of the X coordinate of the intersection list:

sX = StandardDeviation[rootlist[[All, 1]]] // N
81038.5

StandardDeviation[data] - returns the standard deviation of the data, speaking in Russian - the function returns sigma, well, or standard deviation.

We define the same characteristics for the Y coordinate of the intersection:

Ymed = Mean[rootlist[[All, 2]]] // N
sY = StandardDeviation[rootlist[[All, 2]]] // N
-699.907
106488

From the obtained data of mathematical expectations, it is already possible to determine the desired quantities - the angle of rotation of the video camera relative to the edge of the curb:

Xangle = Xang Xmed/Xlen - Xang/2 // N
8.02449

and the angle of the camcorder relative to the trajectories of vehicles

Yangle = Abs[Yang Ymed/Ylen - Yang/2] // N
9.38796

In general, such a large value of the standard deviation is somewhat confusing. we will construct a histogram to look at the distribution of quantities and find out why this happens:

Histogram[
{rootlist[[Range[length], 1]],
rootlist[[Range[length], 2]]},
100, AspectRatio -> 1]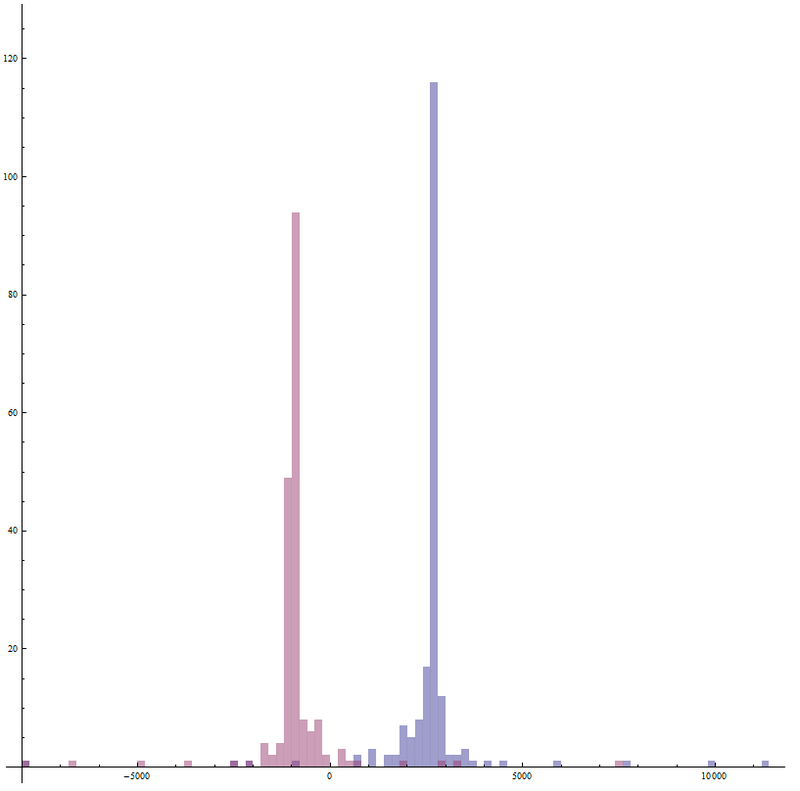


Histogram[list,bspec] - builds a list histogram with the number of bspec columns

From this histogram it can be seen that there are intersection points that are far from the expected value of the quantity.

Let us try not to take into account points that do not satisfy the following conditions:

The X coordinate of the point must lie within [the horizontal resolution of the camera; 2 horizontal camera resolutions]
The Y coordinate of the point must lie within the [- 2 vertical resolution of the camera; 0.5 vertical camera resolution]

To do this, we write the following:

length = Length[rootlist];
rlist = {};
Do[If[
-Xlen < rootlist[[i, 1]] < 2 Xlen && -2 Ylen < rootlist[[i, 2]] < 0.5 Ylen,
rlist = Append[rlist, rootlist[[i]]]]
, {i, length}]

If[condition, t, f] - returns t if the result of the calculation condition is True , and gives f , if the result is False

And[p,q,...] or p && q && ... - logical addition - operation "And";

Let us estimate the expectation and standard deviation of the resulting filtered sample:

Xmed = Mean[rlist[[Range[length], 1]]] // N
Ymed = Mean[rlist[[Range[length], 2]]] // N
sX = StandardDeviation[rlist[[Range[length], 1]]] // N
sY = StandardDeviation[rlist[[Range[length], 2]]] // N
2628.84
-928.819
353.112
457.717

The resulting spread of the filtered sample is smaller than that of the full sample. Determine the desired angles can be the same as in the case of a full sample.

Graphical presentation of results

Now let's display on one graph the intersection points of the filtered sample and the distribution function of the X coordinate of the intersection points:

lp = ListPlot[rlist, PlotStyle -> PointSize[0.0005], GridLines -> {{Xlen, Xmed}, {Ylen, Ymed}}, AspectRatio -> Automatic];
dp = Plot[-1000000 PDF[NormalDistribution[Xmed, sX], x], {x,1000, 4000}, PlotStyle -> {Red}];
Show[lp, dp, PlotRange -> {{0, 4000}, {-2000, 1000}}, AxesOrigin -> {0, 0}]



PDF[dist,x] - returns the value of the probability density of the distribution with the argument x and the given distribution law dist

NormalDistribution[mu,sigma] - normal distribution

I cheated a little and put the coefficient -1000000 for clarity of the schedule.

What's next?

In the next article, I will show a different way to determine the intersection point based on filtering equations and finding subsets within a set.