MSNW thermonuclear rocket
Happy Cosmonautics Day! After reading the post “Building a thermonuclear space engine under the auspices of NASA , ” I decided to find more detailed information about this project. Next, I want to talk about what this engine is, and how it works.

For a start, a little introduction to what fusion fuel is and how it can be used.
')
Energy can be obtained by breaking large unstable atoms into smaller pieces, or by merging two or more small atoms into one large one. In all cases, if we weigh the initial atoms and compare them with the weight of the result, we can find that the final mass will be less. This phenomenon is known as a mass defect and represents the amount of matter that turns into energy. Everyone knows that
According to the convention 1 amu ( atomic mass unit ) = 931.494028 MeV .
Note that thermonuclear fusion produces energy as it merges larger and larger atoms, until they grow to such an extent that they become iron atoms. After that, the fusion of heavy atoms begins to consume more energy than it produces.
This table provides symbols for various particles that can be used as fusion fuel. The masses of particles are given in case you want to calculate the mass defect for the reactions listed below and be surprised at the amount of energy received.
The tritium half-life is only 12.32 years, which makes it a little difficult to use it in space, since after twelve years it will half decay to helium-3. That is why there are no natural deposits of tritium. Most tritium reactor projects rely on tritium generators. They are usually lithium tanks surrounding the reactor. Lithium absorbs neutrons and transmutes into fresh tritium and helium-4.
The famous helium-3, which is often called the economic motive for space exploration, is unfortunately not as good as one might expect. First, it is absent on Earth, because of which it is difficult to mine. Some enthusiasts want to mine it on the moon without specifying its concentration there is very small. To produce only tons of helium-3, it is necessary to process 100 million tons of lunar regolith. Alternatively, it can be produced in factories, but this requires a large number of neutrons. In general, you need to get tritium and wait for it to disintegrate. Huge quantities of helium-3 are available in the atmosphere of Saturn and Uranus, but to extract it from there, an appropriate infrastructure is needed. The concentration of helium-3 in their atmospheres can reach ten parts per million, which is much better than on the moon. Jupiter also contains helium-3 in its atmosphere, but, due to the huge gravity, its extraction can be very complicated.
The Reaction column lists the initial and final reaction products. The MeV / reaction column shows how much energy is released as a result of one reaction in MeV. The TJ / kg column shows how much terajoules (10 12 ) of energy will be released as a result of burning a kilogram of fuel. For comparison, 1 kiloton of TNT ≈ 4.1840 TJ. In 1 TW burning, it is indicated how many grams of fuel must be burned every second to produce 1 TW of thermal energy. The KL column shows the Lawson criteria for this reaction. Without a neutron, it says whether a reaction produces neutrons or not. It should be noted that if even neutrons do not appear in the reaction, they can still be formed as a result of side reactions. And the Exhaust column gives an idea of the theoretically maximum rate of discharge of combustion products as a percentage of the speed of light. It is assumed that all the energy obtained in the course of the reaction is converted into the kinetic energy of the motion of the reaction products.
There are quite a few thermonuclear reactions, but only a small number of them are suitable for use as energy sources for rocket engines. About the restrictions can be read here . Of all the candidates, the easiest to use are reactions with a low Lawson criterion by which one can judge the difficulty of starting and maintaining a reaction. If the reaction produces only charged particles, then this can be considered a big plus, since it becomes possible to convert them into electricity directly, without an intermediary, in the form of heat.
It is also desirable that the reaction does not produce neutrons, since they are not only dangerous radiation, but also tend to weaken the materials of construction and transmute parts of the engine into radioactive elements . Unless, of course, there is no need to use neutrons to produce tritium.
The D + 3 He reaction is particularly interesting for use in rocket engines, since its products are only charged particles, which makes it possible to directly control them using a magnetic nozzle.
The table shows that there are various reactions that look promising for use in space and on Earth. Note that the D + D reaction has two possible results and, accordingly, two rows in the table. Each result has a probability of 50%. Two reactions with lithium do not produce energy and are used to produce tritium, as mentioned above.
The DT reaction is relatively easy to start, as indicated by Lawson's low criterion, but it consumes tritium with a short half-life. A hydrogen-boric reaction (a proton is an ionized hydrogen atom) has the advantage of not producing neutrons, but it is very difficult to ignite. Helium-3 + helium-3 is also neutron-free, but helium-3 is difficult to produce. Apparently because of this, information on the Lawson criteria for this reaction could not be found.
The proton-proton reaction takes place on the sun. The problem is the highest Lawson criteria from the entire table. It is almost impossible to make four protons merge; it is easier to use an existing star for energy.
Two reactions with lithium do not produce any energy and are usually used to produce tritium.
Based on the Mission Design Architecture for the Fusion Driven Rocket. Pancotti, A., Slough, J. Kirtley, D. et al. AIAA Joint Propulsion Conference (2012) .
This article describes, at first glance, another way to use fusion energy for the implementation of fast manned space flights. Previous efforts on this path have been fruitless, largely due to the following two reasons. First, they were based on the design of fusion reactors. Rectilinear application of the approaches used in reactors leads to systems with a huge mass and problems with energy removal. With a detailed analysis for the most compact concept of TOKMAK, a spherical torus, the weight of the ship was about 4000 tons. The maximum mass for launching into a low reference orbit using chemical rockets should not exceed 200 tons.
The second reason is that, in fact, all previous propulsion systems required complex reactions that produce, for the most part, charged particles. This was necessary to reduce the energy loss through neutrons. The most promising were D- 3 He and P- 11 B. But these reactions require much higher plasma temperatures and were orders of magnitude more difficult to achieve than DT synthesis, which is much more accessible and considered the only candidate for use on Earth. Being less profitable, they nevertheless require a huge amount of energy to sustain combustion, making them no better than alternative fission reactions.
It is necessary to rethink past ideas about how to use thermonuclear energy in space propulsion systems. Let's see what gives chemical rocket engines such advantages. The main reason is that the energy obtained from a chemical combustion reaction can be both large and small, if desired. From 13 GW in heavy Atlas launch vehicle, up to 130 kW in vehicle. It is worth noting that with lower energy, combustion is more efficient, since it is possible to raise the temperature without worrying about the need for intensive heat removal and thermal damage that may occur during long-term continuous operation.
As tests of atomic and hydrogen bombs have shown, the burning of a nuclear fuel can produce energy by many orders of magnitude greater than the same Atlas. The problem is how to control the release of nuclear energy to obtain the characteristics required for space flights: a torch of several megawatts, a low specific gravity
Fortunately, the scale of thermonuclear reactions can be much smaller, and methods such as Magneto Inertial Fusion (MIF) can produce large amounts of energy from nuclear material in systems that can be suitable for space propulsion systems, weight, power and cost.
The engine is based on the three-dimensional implosion principle (shock wave compression) of metal foil around a plasmoid FRC ( Field-reversed configuration - field with reversed configuration) using a magnetic field. This is necessary to achieve the conditions necessary for the start of the synthesis, such as high temperature and pressure. This approach to launching a reaction is a type of inertial synthesis. In order to get an idea of how it works, you can take a look at inertial controlled thermonuclear fusion (ICF). ICF synthesis is achieved using a three-dimensional implosion of a spherical capsule with cryogenic fuel of millimeter size. Implosion occurs due to the explosive evaporation of the capsule body, after it is heated with the help of laser beams, electrons, or ions. The heated outer layer of the capsule explodes in an external direction, which produces a counteracting force that accelerates the rest of the material of the capsule inward, compressing it. Also, shock waves moving inside the target appear. With a sufficiently powerful set of shock waves, it can compress and heat the fuel in the center so much that it starts a thermonuclear reaction. In this method, it is assumed that the inertia of a small capsule is enough to hold the plasma long enough for all the fuel to react and produce a useful output of G ~ 200 or more (G = synthesis energy / plasma energy). The ICF approach has been pursued by the National Nuclear Security Administration (NNSA) for decades, as it represents something like a miniature thermonuclear bomb. Due to the small size and weight, the heating of the capsule to the synthesis temperature should be carried out within nanoseconds. It turned out that the most promising solution to this problem is an array of high-power pulsed lasers focused on a capsule with DT fuel.
The National Ignition Facility (NIF) at the Livermore National Laboratory is conducting experiments on laser fusion of a capsule with a thermonuclear fuel, but attempts have so far not been very successful.
However, for use in space, other approaches are needed. This means that the use of huge laser systems will have to be abandoned. Heavy ions and crimped metal shells are the two most promising technologies. Regardless of the method, the reduction should be uniform, strong and carried out with great precision, which can lead to large, high-voltage and very expensive systems. In the mid-nineties, it was found that the presence of a strong magnetic field significantly suppresses the transfer of heat in the target, which reduces the power of the implosion required to compress the target and start synthesis therein. Long before the thermal energy of the plasma is dissipated, a metal sheath can be used for direct compression. So we can increase the time of thermonuclear burning, thanks to the bounding metal shell. The shell can be compressed both with the help of explosives, and with the help of a magnetic field. It was shown that if the implosion of the shell around the magnetized target was completely three-dimensional, then the energy gain can be obtained on a small scale with the kinetic energy of the shell up to 1 MJ.
At that time there was no known way to achieve all this in practice. But in 2000 it was shown that for a sufficiently magnetized target plasma, thermonuclear burning can begin even when the restriction
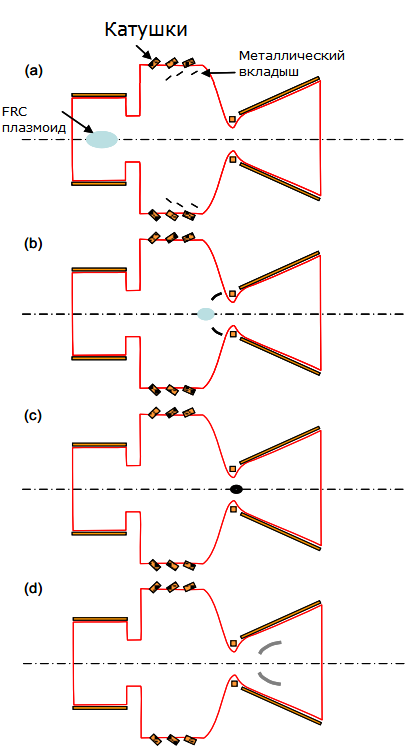
Schematic representation of the process of inductive implosion of a plasmoid FRC with a metal insert. (a) Thin metal hoops start moving at such a speed and in such a direction as to compress the plasmoid in the throat of the nozzle. An FRC plasmoid acting as a target is fired at the engine chamber. (b) The FRC plasmoid is held by a longitudinal magnetic field from contact with the walls of the chamber during its movement to the throat of the nozzle. (c) The insert segments compress the FRC plasmoid, which results in conditions for the start of a thermonuclear reaction. (d) Under the action of alpha particles and neutrons produced by a thermonuclear reaction, the liner evaporates and turns into an ionized plasma, which expands along a diverging magnetic field. This leads to the direct generation of electricity, due to the back EMF, and directed thrust from the outflow of plasma from the magnetic nozzle.
It was clear that the conditions for the start of a thermonuclear reaction could be achieved on a small scale due to the kinetic energy of a massive metal liner aimed at compressing the plasma in the target to a high density and temperature. But to translate this into reality, it was necessary to answer the following questions:
The key to answering all these four questions may be the study of magnetic three-dimensional compression of metal rings around a FRC target to obtain a thermonuclear reaction, recently conducted in MSNW . The logical continuation of these studies is the method that uses these metal rings not only to achieve the necessary conditions for the start of combustion, but also for the direct creation of thrust. To answer the first two questions, it is necessary to achieve high efficiency of the installation and achieve a “stand-off” - the ability to protect the structure and fuel from the energy released by the reaction. A converging motion of metal rings can be achieved using inductance, for which you need to place them along the inner surface of cylindrical or conical wedge-shaped coils. This solves problems with both efficiency and stand-off. The metal insert can be located at a distance of up to a meter from the target. Moreover, the coils can be isolated both physically and electrically. The efficiency of the drive can be extremely high, since the coils in it are an inductive element in a simple oscillatory circuit, where the resistance losses are extremely small compared to the energy transferred. Using even simple elements such as an array of diodes, any magnetic energy that is not transferred to the liner can be returned to the charger after the shell is ejected through the nozzle after the first half of the cycle.
, , , , , , , 600 . , FRC .
. , . , , , , (FRC). ,
3 /, FRC 0.2 , , 67 , FRC (~ 1 ).
, . , . , (r > 5 ) , , . , , , . , , - . , , .

1 2 .
, , , Δv — (/ /). «», , . , , , , Δv. Δv , , , . , «» , , Δv . , , Goman trajectory to Mars and landing on it, requires a budget Δv at 18 km / s. If the ship has a Δv reserve greater than or equal to Δv of the mission, then it can complete this mission.
In order to learn Δv of a ship, you can use the formula of Tsiolkovsky .
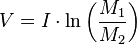
Where:
V — ( ) (/);
I — ( , , /);
M 1 — ( + + , );
M 2 — ( + , ).
, . Δv , , . , Δv , , . , - .
210- .

: .
Benefits:
: .
Benefits:
NASA (Space Launch System, SLS) — -, 70 130 . 90- -.
.
, , 0.1 . , 51400 /, 0,37 , p = mv = 19018 ·/. , p/M = 19018/133000 = 0.14 /. 1 , t = r/v =1/51400 =0,00002 . a = dv/dt = 0,14/0,00002 = 7000 / 2 . , , , - .

For a start, a little introduction to what fusion fuel is and how it can be used.
')
Thermonuclear fuel
Energy can be obtained by breaking large unstable atoms into smaller pieces, or by merging two or more small atoms into one large one. In all cases, if we weigh the initial atoms and compare them with the weight of the result, we can find that the final mass will be less. This phenomenon is known as a mass defect and represents the amount of matter that turns into energy. Everyone knows that
e = mc^2 , but not all represent how much c (the speed of light in a vacuum ) is a large number, and when squared it becomes just very large. Accordingly, even a microscopic amount of a substance becomes capable of producing an impressive amount of energy.According to the convention 1 amu ( atomic mass unit ) = 931.494028 MeV .
Example.
DT synthesis begins with a deuterium and tritium atom and ends with a helium-4 atom and a neutron. The initial mass is 2.013553 + 3.015500 = 5.029053. The final mass is 4.001506 + 1.008665 = 5.010171. Subtracting the second from the first, we find that the mass defect is equal to 0.018882. Multiplying by 931.494028 we find the resulting energy equal to 17.58847 MeV.
Note that thermonuclear fusion produces energy as it merges larger and larger atoms, until they grow to such an extent that they become iron atoms. After that, the fusion of heavy atoms begins to consume more energy than it produces.
Particles
| Symbol | Title | Weight |
|---|---|---|
| p | Proton, ionized hydrogen | 1.007276 |
| n | Neutron | 1.008665 |
| 1 H | Hydrogen-1, ordinary hydrogen | 1.007940 |
| D | Deuterium, hydrogen-2 | 2.013553 |
| T | Tritium, hydrogen-3 | 3.015500 |
| 3 He | Famous helium-3 | 3.014932 |
| 4 He | Helium-4, ordinary helium | 4.001506 |
| 6 Li | Lithium-6 | |
| 7 li | Lithium-7, ordinary lithium | |
| 11 B | Boron-11, conventional boron | 11.00931 |
This table provides symbols for various particles that can be used as fusion fuel. The masses of particles are given in case you want to calculate the mass defect for the reactions listed below and be surprised at the amount of energy received.
The tritium half-life is only 12.32 years, which makes it a little difficult to use it in space, since after twelve years it will half decay to helium-3. That is why there are no natural deposits of tritium. Most tritium reactor projects rely on tritium generators. They are usually lithium tanks surrounding the reactor. Lithium absorbs neutrons and transmutes into fresh tritium and helium-4.
The famous helium-3, which is often called the economic motive for space exploration, is unfortunately not as good as one might expect. First, it is absent on Earth, because of which it is difficult to mine. Some enthusiasts want to mine it on the moon without specifying its concentration there is very small. To produce only tons of helium-3, it is necessary to process 100 million tons of lunar regolith. Alternatively, it can be produced in factories, but this requires a large number of neutrons. In general, you need to get tritium and wait for it to disintegrate. Huge quantities of helium-3 are available in the atmosphere of Saturn and Uranus, but to extract it from there, an appropriate infrastructure is needed. The concentration of helium-3 in their atmospheres can reach ten parts per million, which is much better than on the moon. Jupiter also contains helium-3 in its atmosphere, but, due to the huge gravity, its extraction can be very complicated.
Thermonuclear reactions
| Reaction | MeV / reaction | TJ / kg | 1 TW burning | KL | Without neutron | Exhaust | ||
|---|---|---|---|---|---|---|---|---|
| D + T | ⇒ | 4 He + n | 17.6 MeV | 339.72 TJ / kg | 0.002944 g / s | one | 8.7% c | |
| D + D | ⇒ | T + 1 h | 4.03 MeV | 97.23 TJ / kg | 0.01028 g / s | thirty | 4.3% c | |
| 3 He + n | 3.27 MeV | 78.90 TJ / kg | 0.01267 g / s | 4.2% c | ||||
| p + 11 B | ⇒ | 3 × 4 He | 8.7 MeV | 69.97 TJ / kg | 0.01429 g / s | 500 | Yes | 4.5% c |
| D + 3 He | ⇒ | 4 He + p | 18.3 MeV | 353.23 TJ / kg | 0.002831 g / s | sixteen | 8.9% c | |
| 3 He + 3 He | ⇒ | 4 He + 2 × p | 12.9 MeV | 207.50 TJ / kg | 0.004819 g / s | ? | Yes | 6.8% c |
| n + 6 Li | ⇒ | T + 4 He | ||||||
| n + 7 Li | ⇒ | T + 4 He + n | ||||||
| p + p + p + p | ⇒ | 4 He | 26.73 MeV | 644.93 TJ / kg | 0.001551 g / s | Lot | 11.7% c | |
The Reaction column lists the initial and final reaction products. The MeV / reaction column shows how much energy is released as a result of one reaction in MeV. The TJ / kg column shows how much terajoules (10 12 ) of energy will be released as a result of burning a kilogram of fuel. For comparison, 1 kiloton of TNT ≈ 4.1840 TJ. In 1 TW burning, it is indicated how many grams of fuel must be burned every second to produce 1 TW of thermal energy. The KL column shows the Lawson criteria for this reaction. Without a neutron, it says whether a reaction produces neutrons or not. It should be noted that if even neutrons do not appear in the reaction, they can still be formed as a result of side reactions. And the Exhaust column gives an idea of the theoretically maximum rate of discharge of combustion products as a percentage of the speed of light. It is assumed that all the energy obtained in the course of the reaction is converted into the kinetic energy of the motion of the reaction products.
There are quite a few thermonuclear reactions, but only a small number of them are suitable for use as energy sources for rocket engines. About the restrictions can be read here . Of all the candidates, the easiest to use are reactions with a low Lawson criterion by which one can judge the difficulty of starting and maintaining a reaction. If the reaction produces only charged particles, then this can be considered a big plus, since it becomes possible to convert them into electricity directly, without an intermediary, in the form of heat.
It is also desirable that the reaction does not produce neutrons, since they are not only dangerous radiation, but also tend to weaken the materials of construction and transmute parts of the engine into radioactive elements . Unless, of course, there is no need to use neutrons to produce tritium.
The D + 3 He reaction is particularly interesting for use in rocket engines, since its products are only charged particles, which makes it possible to directly control them using a magnetic nozzle.
The table shows that there are various reactions that look promising for use in space and on Earth. Note that the D + D reaction has two possible results and, accordingly, two rows in the table. Each result has a probability of 50%. Two reactions with lithium do not produce energy and are used to produce tritium, as mentioned above.
The DT reaction is relatively easy to start, as indicated by Lawson's low criterion, but it consumes tritium with a short half-life. A hydrogen-boric reaction (a proton is an ionized hydrogen atom) has the advantage of not producing neutrons, but it is very difficult to ignite. Helium-3 + helium-3 is also neutron-free, but helium-3 is difficult to produce. Apparently because of this, information on the Lawson criteria for this reaction could not be found.
The proton-proton reaction takes place on the sun. The problem is the highest Lawson criteria from the entire table. It is almost impossible to make four protons merge; it is easier to use an existing star for energy.
Two reactions with lithium do not produce any energy and are usually used to produce tritium.
Thermonuclear rocket engine
Based on the Mission Design Architecture for the Fusion Driven Rocket. Pancotti, A., Slough, J. Kirtley, D. et al. AIAA Joint Propulsion Conference (2012) .
Introduction
This article describes, at first glance, another way to use fusion energy for the implementation of fast manned space flights. Previous efforts on this path have been fruitless, largely due to the following two reasons. First, they were based on the design of fusion reactors. Rectilinear application of the approaches used in reactors leads to systems with a huge mass and problems with energy removal. With a detailed analysis for the most compact concept of TOKMAK, a spherical torus, the weight of the ship was about 4000 tons. The maximum mass for launching into a low reference orbit using chemical rockets should not exceed 200 tons.
The second reason is that, in fact, all previous propulsion systems required complex reactions that produce, for the most part, charged particles. This was necessary to reduce the energy loss through neutrons. The most promising were D- 3 He and P- 11 B. But these reactions require much higher plasma temperatures and were orders of magnitude more difficult to achieve than DT synthesis, which is much more accessible and considered the only candidate for use on Earth. Being less profitable, they nevertheless require a huge amount of energy to sustain combustion, making them no better than alternative fission reactions.
It is necessary to rethink past ideas about how to use thermonuclear energy in space propulsion systems. Let's see what gives chemical rocket engines such advantages. The main reason is that the energy obtained from a chemical combustion reaction can be both large and small, if desired. From 13 GW in heavy Atlas launch vehicle, up to 130 kW in vehicle. It is worth noting that with lower energy, combustion is more efficient, since it is possible to raise the temperature without worrying about the need for intensive heat removal and thermal damage that may occur during long-term continuous operation.
As tests of atomic and hydrogen bombs have shown, the burning of a nuclear fuel can produce energy by many orders of magnitude greater than the same Atlas. The problem is how to control the release of nuclear energy to obtain the characteristics required for space flights: a torch of several megawatts, a low specific gravity
α (~ 1 kg / kW) with a high specific impulse Isp (> 20000 m / s). It turned out that, at least for nuclear fission, there is no possibility of scaling down to the required energy scale, since a certain critical mass (critical configuration) is required to start a self-sustaining reaction. As a result, projects using nuclear fission reactions, such as Orion, usually yielded millions of tons, which is only suitable for spacecraft with a mass of 10 7 kg and above.Fortunately, the scale of thermonuclear reactions can be much smaller, and methods such as Magneto Inertial Fusion (MIF) can produce large amounts of energy from nuclear material in systems that can be suitable for space propulsion systems, weight, power and cost.
Engine physics
The engine is based on the three-dimensional implosion principle (shock wave compression) of metal foil around a plasmoid FRC ( Field-reversed configuration - field with reversed configuration) using a magnetic field. This is necessary to achieve the conditions necessary for the start of the synthesis, such as high temperature and pressure. This approach to launching a reaction is a type of inertial synthesis. In order to get an idea of how it works, you can take a look at inertial controlled thermonuclear fusion (ICF). ICF synthesis is achieved using a three-dimensional implosion of a spherical capsule with cryogenic fuel of millimeter size. Implosion occurs due to the explosive evaporation of the capsule body, after it is heated with the help of laser beams, electrons, or ions. The heated outer layer of the capsule explodes in an external direction, which produces a counteracting force that accelerates the rest of the material of the capsule inward, compressing it. Also, shock waves moving inside the target appear. With a sufficiently powerful set of shock waves, it can compress and heat the fuel in the center so much that it starts a thermonuclear reaction. In this method, it is assumed that the inertia of a small capsule is enough to hold the plasma long enough for all the fuel to react and produce a useful output of G ~ 200 or more (G = synthesis energy / plasma energy). The ICF approach has been pursued by the National Nuclear Security Administration (NNSA) for decades, as it represents something like a miniature thermonuclear bomb. Due to the small size and weight, the heating of the capsule to the synthesis temperature should be carried out within nanoseconds. It turned out that the most promising solution to this problem is an array of high-power pulsed lasers focused on a capsule with DT fuel.
The National Ignition Facility (NIF) at the Livermore National Laboratory is conducting experiments on laser fusion of a capsule with a thermonuclear fuel, but attempts have so far not been very successful.
However, for use in space, other approaches are needed. This means that the use of huge laser systems will have to be abandoned. Heavy ions and crimped metal shells are the two most promising technologies. Regardless of the method, the reduction should be uniform, strong and carried out with great precision, which can lead to large, high-voltage and very expensive systems. In the mid-nineties, it was found that the presence of a strong magnetic field significantly suppresses the transfer of heat in the target, which reduces the power of the implosion required to compress the target and start synthesis therein. Long before the thermal energy of the plasma is dissipated, a metal sheath can be used for direct compression. So we can increase the time of thermonuclear burning, thanks to the bounding metal shell. The shell can be compressed both with the help of explosives, and with the help of a magnetic field. It was shown that if the implosion of the shell around the magnetized target was completely three-dimensional, then the energy gain can be obtained on a small scale with the kinetic energy of the shell up to 1 MJ.
At that time there was no known way to achieve all this in practice. But in 2000 it was shown that for a sufficiently magnetized target plasma, thermonuclear burning can begin even when the restriction
ρ⋅R > 0.1 / 2 (R is the target radius, ρ is the target density) is not satisfied. Combustion became possible for as long as B⋅R > 60 ⋅ (B is magnetic induction). Consequently, combustion can be obtained at a much lower pressure than in the ICF. The final element necessary for effective use in space remains the method of converting the released energy into thrust while maintaining a high specific impulse.
Schematic representation of the process of inductive implosion of a plasmoid FRC with a metal insert. (a) Thin metal hoops start moving at such a speed and in such a direction as to compress the plasmoid in the throat of the nozzle. An FRC plasmoid acting as a target is fired at the engine chamber. (b) The FRC plasmoid is held by a longitudinal magnetic field from contact with the walls of the chamber during its movement to the throat of the nozzle. (c) The insert segments compress the FRC plasmoid, which results in conditions for the start of a thermonuclear reaction. (d) Under the action of alpha particles and neutrons produced by a thermonuclear reaction, the liner evaporates and turns into an ionized plasma, which expands along a diverging magnetic field. This leads to the direct generation of electricity, due to the back EMF, and directed thrust from the outflow of plasma from the magnetic nozzle.
It was clear that the conditions for the start of a thermonuclear reaction could be achieved on a small scale due to the kinetic energy of a massive metal liner aimed at compressing the plasma in the target to a high density and temperature. But to translate this into reality, it was necessary to answer the following questions:
- How to do this without huge magnetic coils?
- How to make it effective and repeatable?
- How to create a suitable plasmoid used as a target?
- How to convert thermonuclear reaction energy into directional cravings?
The key to answering all these four questions may be the study of magnetic three-dimensional compression of metal rings around a FRC target to obtain a thermonuclear reaction, recently conducted in MSNW . The logical continuation of these studies is the method that uses these metal rings not only to achieve the necessary conditions for the start of combustion, but also for the direct creation of thrust. To answer the first two questions, it is necessary to achieve high efficiency of the installation and achieve a “stand-off” - the ability to protect the structure and fuel from the energy released by the reaction. A converging motion of metal rings can be achieved using inductance, for which you need to place them along the inner surface of cylindrical or conical wedge-shaped coils. This solves problems with both efficiency and stand-off. The metal insert can be located at a distance of up to a meter from the target. Moreover, the coils can be isolated both physically and electrically. The efficiency of the drive can be extremely high, since the coils in it are an inductive element in a simple oscillatory circuit, where the resistance losses are extremely small compared to the energy transferred. Using even simple elements such as an array of diodes, any magnetic energy that is not transferred to the liner can be returned to the charger after the shell is ejected through the nozzle after the first half of the cycle.
, , , , , , , 600 . , FRC .
. , . , , , , (FRC). ,
β ( / ) . , FRC . , FRC , . FRC , B⋅R .3 /, FRC 0.2 , , 67 , FRC (~ 1 ).
, . , . , (r > 5 ) , , . , , , . , , - . , , .

1 2 .
, , , Δv — (/ /). «», , . , , , , Δv. Δv , , , . , «» , , Δv . , , Goman trajectory to Mars and landing on it, requires a budget Δv at 18 km / s. If the ship has a Δv reserve greater than or equal to Δv of the mission, then it can complete this mission.
In order to learn Δv of a ship, you can use the formula of Tsiolkovsky .
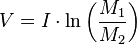
Where:
V — ( ) (/);
I — ( , , /);
M 1 — ( + + , );
M 2 — ( + , ).
, . Δv , , . , Δv , , . , - .
210- .

90- (ΔV = 13.5 /)
: .
Benefits:
30- (ΔV = 40.9 /)
: .
Benefits:
- ,
| ( 200) | 90 days | 30 days |
|---|---|---|
| () | 2.6 | 33 |
| () | 27 | 350 |
| () | 5140 | 5140 |
| (/) | 4,3 | 0.38 |
| () | 90 | 153 |
| 65% | 36% |
NASA (Space Launch System, SLS) — -, 70 130 . 90- -.
.
| , | |
|---|---|
| 75 / | |
| ( ) | 50% |
| η t | 90% |
| ( 50 500) | 0,28 0,41 |
| five | |
| (G F =G F(calc.) /2) | 2 |
| , | |
| ( Design Reference Architecture 5.0) | 61 |
| • | 31 |
| • | 16 |
| • | 14 |
| ( ) | 1 / |
| 200 / | |
| (, , .) | ten% |
| , | |
| (, , , , ) | 6,6 |
| 0,1 | |
| 0,2 | |
| 1,2 | |
| 1,8 | |
| 0,3 | |
| 1,8 | |
| (180 200 /) | 1,5 |
| 1,3 | |
| 0,2 | |
| 15 | |
| 61 | |
| 57 | |
| 133 | |
, , 0.1 . , 51400 /, 0,37 , p = mv = 19018 ·/. , p/M = 19018/133000 = 0.14 /. 1 , t = r/v =1/51400 =0,00002 . a = dv/dt = 0,14/0,00002 = 7000 / 2 . , , , - .
Source: https://habr.com/ru/post/176271/
All Articles