Briefly about hydrodynamics: energy conservation
Once again, I apologize for the slow writing posts in the planned series. This time the reason for the delay is objective, in the form of a conference in Vienna, although it has a significant subjective component in the form of its own participation and some bureaucratic moments of preparation and payment.
This post considers the laws of energy conservation in an ideal and viscous fluid. They are obviously necessary for the completeness of motion description, however, in the isothermal case, there is no heat exchange as such, and therefore it is sufficient to use the Navier-Stokes equation and the continuity equation for the description. I hope this post will be the last of the rather abstract posts that describe the general theory and are not practically tied to specific problem statements.
Previous posts:
Briefly about hydrodynamics: do you remember how it all began?
Briefly about hydrodynamics: equations of motion
')
I will try to reduce the number of calculations, because they, of course, are important, but the results in the form of finite equations are more important.
So, the conservation of energy. The approach to the description is absolutely standard - we introduce some value, find which mechanisms are responsible for changing it and write the conservation law first in integral form, and then, reducing all surface integrals to the bulk one according to the Gauss theorem - in the differential one.
The energy of a fluid in classical hydrodynamics, which also disregards such an effect as electrical conductivity and the corresponding interaction with external and internal electromagnetic fields, is made up of internal and kinetic energy. It is equal to such an integral:
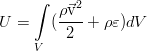
Energy can change within our volume V due to its simple flow with the flow of fluid, the work of pressure forces from external elements of the fluid and the work of external forces (shown below on the example of gravity):
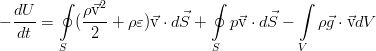
In an ideal fluid, there is no friction, and therefore there is no energy dissipation due to viscosity. In addition, heat conduction processes are also neglected here, which is also inherent in an ideal fluid as the absence of one more energy dissipation mechanism. In differential form, the law of conservation of total energy is as follows:
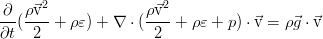
However, it can be safely simplified. Using the Euler equation (see the previous post ), scalarly multiplied by the speed, we can distinguish the following part from the obtained conservation law:
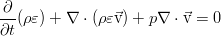
And this is already transformed to an even simpler form:
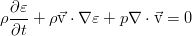
Here you can remember the thermodynamics. The first law of thermodynamics (with a mark — for a specific volume of a fluid, i.e. a volume whose mass is equal to one):
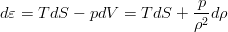
allows one to quite obviously connect the derivatives of energy, entropy and density (as an inverse of a quantity). Using this relationship of differentials in the equation for energy:
as well as the law of conservation of mass, we obtain another equation that describes the evolution of entropy in a liquid:
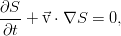
In a moving frame of reference, attached to the fluid element for which it is all written, the equation is simplified even more:
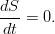
That is, the entropy of a separate arbitrary liquid particle (in an ideal fluid) is preserved. Entropy is simply passively carried by the flow, simultaneously connecting pressure and density of the medium by the equation of state.
Now we take into account the viscous and heat conductive dissipation. In the integral form, they are represented by a pair of additional components in the law of conservation:
They describe the work of viscous friction forces on the boundary of the fluid element and the heat flux through the boundary. In differential form, the total energy conservation equation:
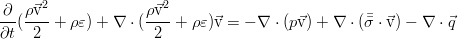
Having performed a series of operations on this ratio using the momentum transfer equation in general form (for an arbitrary viscous stress tensor) and the continuity equation (namely, multiplying the mass conservation law by half the square of the velocity, the momentum conservation law by the velocity, adding them together and subtracting total of the equation for total energy), we get rid of the addends with kinetic energy:
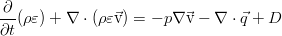
Here a dissipative function arises, equal to the double convolution of the viscous stress tensor and the tensor, which is conventionally sometimes called the velocity gradient:
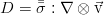
Applying here the mass balance equation and the first law of thermodynamics, in the same way as was done above, we arrive at the entropy balance equation:
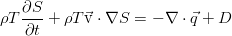
It can be seen that it differs from the equation in an ideal fluid only in the non-zero right-hand side. For an incompressible fluid, we can safely move from entropy to a more tangible value, that is, to temperature, using the definition of heat capacity at constant pressure:
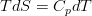
Finally, we can neglect the dissipative function, since it describes the selection due to internal friction, and therefore it is essential only in liquids with very large viscosities, and for the heat flux to use the Fourier thermal conductivity law, which allows expressing it through temperature:
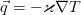
As a result, we obtain the heat conduction equation for an incompressible viscous fluid:
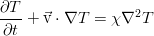
According to it, the temperature of the fluid element changes due to direct convective transport with the fluid flow, as well as due to the quite usual mechanism of molecular heat conduction (right side).
Actually, with the description of the convection problem in Habré , this whole hydrodynamic "booth" began. So, we look at a jar with an incompressible viscous liquid, for example, water. Its motion in the case of non-uniform temperature in the volume is described by three equations:
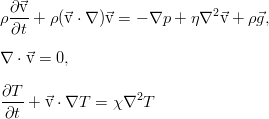
In the general case, this system also includes a state equation relating density, pressure, and temperature. However, then the fluid can no longer be considered incompressible. Practice (and mathematics) shows that with sufficient accuracy one can accept density constant everywhere, except for the term with the force of gravity. Moreover, it suffices to restrict ourselves to linear temperature decomposition:
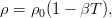
Immediately, we note that there is no longer recorded the absolute temperature, but already a deviation from some "zero" level, at which the density is equal to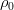
. To write this way allows us the equation of heat conduction, since it is linear and is invariant to such shifts. In the term of gravity, it is possible to isolate a part independent of temperature (hydrostatic gradient) and hide it in pressure:
And then we come to the convection equations in the Boussinesq approximation:
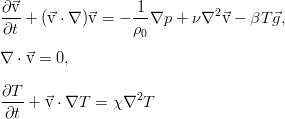
This model is practically common when studying convective phenomena, and on its basis a huge number of very different results were obtained. In particular, in problems of stability of equilibrium of fluid and others.
I digress a little from the topic, although I understand perfectly well that this can only kindle an extra and distracting discussion.
You know what surprised in the comments on the previous post? The fact that readers pay a lot of attention to the question of mathematical rigor of the calculations, which, in general, is not much here. Hydrodynamics was created by Euler and Navier during the rule of French materialism, when the strict results of analytical mechanics, it seemed, described the whole world. But the level of rigor of these results is as it could be at that time, in the barely created by Newton and other differential calculus, and not higher. And so it remains to this day, and the mathematical rigor of hydrodynamics is the same. In practice, this is the last classical field of science, which still has unsolved fundamental problems. Maybe they are not solved precisely because they are formulated in the old, not very developed and not rich in significant means language. I remember that there are some developments in mathematics, where the apparatus is applied to the Navier-Stokes equations, remember the Bipinorov and Dirac gamma-matrices (the basis of quantum field theory), or worse, at night, or even worse. But they are still separate and virtually unknown.
Personally, I assume that the development of the apparatus for solving the Navier-Stokes equations has simply not yet taken place. As is known, these equations perfectly describe both ordered laminar flows and chaos of turbulence. And in the equations for this just enough to change one control parameter. As in nonlinear systems (a-la Lorentz system ), which also have no common analytical solutions, and, in general, a specific detailed analysis of the properties of solutions precisely as mathematical functions. Much at the level of behavior - there is chaos, there is ordering, there is synchronization, there is the influence of the parameter, and the transition, apparently, happens like this. But there is no question about the smoothness of the solutions, nor about their existence in such problems, unlike Navier-Stokes. After all, we still hardly know whether their general smooth solutions exist at all.
Having seen things like “nabla is a 1-form” in the comments, at first I was seriously thinking about whether I had missed something in my education. Yes, about the various kinds of n-forms I mentioned in the courses (but not more) in one semester special course called group theory in physics, from which, however, a lot was not possible because of the absence of a serious structured presentation. But to argue about whether Nabla is a vector or not, it never happens. In physics, which does not deal with significantly mathematized level problems, say, the general theory of relativity and the inherently necessary differential geometry for it, nabla has always been practically a vector. Of course, not quite ordinary, not commuting with them and possessing a number of other properties. Simple, in general, even an ordinary operator, which shows which component of the vector and how we will differentiate. It's just a tool that we can use within the specified limits and we realize that we need to check its suitability when going beyond the boundary of a familiar area, even, for example, when moving from Cartesian coordinates to the same spherical ones.
Sometimes you can spend too much time understanding the hammer, but never really learn how to hammer nails into them. For example, why it has such a shape, why different hammers have a different shape, and then start digging deeper - why metal glitters and wooden handle doesn’t, etc. But the essence of the most frequent use of a hammer will not change from this understanding. They will hammer nails, level the metal on the mandrel, etc. - they will still be knocked, preferably not on the fingers.
At this level is my personal acquaintance with the apparatus of quantum electrodynamics. By the principle - I remember, something passed. Moreover, even the training manual was published from a distance with a teacher of this subject last year, but somehow it is still aside - I am not doing it.
The next post will be devoted to problems of stability for equilibrium and stationary flow. There once again we will see that even the simplest problems of hydrodynamics cannot be solved analytically in full form, and therefore we have to apply many different, at first glance, very controversial, but at the same time perfectly working and sound methods. I hope that we can already move from abstract to more tangible things.
This post considers the laws of energy conservation in an ideal and viscous fluid. They are obviously necessary for the completeness of motion description, however, in the isothermal case, there is no heat exchange as such, and therefore it is sufficient to use the Navier-Stokes equation and the continuity equation for the description. I hope this post will be the last of the rather abstract posts that describe the general theory and are not practically tied to specific problem statements.
Previous posts:
Briefly about hydrodynamics: do you remember how it all began?
Briefly about hydrodynamics: equations of motion
')
I will try to reduce the number of calculations, because they, of course, are important, but the results in the form of finite equations are more important.
Energy transfer in a perfect fluid
So, the conservation of energy. The approach to the description is absolutely standard - we introduce some value, find which mechanisms are responsible for changing it and write the conservation law first in integral form, and then, reducing all surface integrals to the bulk one according to the Gauss theorem - in the differential one.
The energy of a fluid in classical hydrodynamics, which also disregards such an effect as electrical conductivity and the corresponding interaction with external and internal electromagnetic fields, is made up of internal and kinetic energy. It is equal to such an integral:
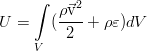
Energy can change within our volume V due to its simple flow with the flow of fluid, the work of pressure forces from external elements of the fluid and the work of external forces (shown below on the example of gravity):
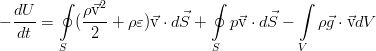
In an ideal fluid, there is no friction, and therefore there is no energy dissipation due to viscosity. In addition, heat conduction processes are also neglected here, which is also inherent in an ideal fluid as the absence of one more energy dissipation mechanism. In differential form, the law of conservation of total energy is as follows:
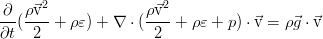
However, it can be safely simplified. Using the Euler equation (see the previous post ), scalarly multiplied by the speed, we can distinguish the following part from the obtained conservation law:
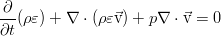
And this is already transformed to an even simpler form:
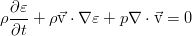
Here you can remember the thermodynamics. The first law of thermodynamics (with a mark — for a specific volume of a fluid, i.e. a volume whose mass is equal to one):
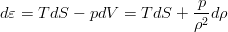
allows one to quite obviously connect the derivatives of energy, entropy and density (as an inverse of a quantity). Using this relationship of differentials in the equation for energy:
as well as the law of conservation of mass, we obtain another equation that describes the evolution of entropy in a liquid:
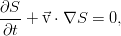
In a moving frame of reference, attached to the fluid element for which it is all written, the equation is simplified even more:
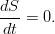
That is, the entropy of a separate arbitrary liquid particle (in an ideal fluid) is preserved. Entropy is simply passively carried by the flow, simultaneously connecting pressure and density of the medium by the equation of state.
Viscosity accounting. Heat equation
Now we take into account the viscous and heat conductive dissipation. In the integral form, they are represented by a pair of additional components in the law of conservation:
They describe the work of viscous friction forces on the boundary of the fluid element and the heat flux through the boundary. In differential form, the total energy conservation equation:
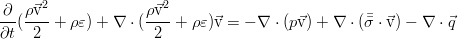
Having performed a series of operations on this ratio using the momentum transfer equation in general form (for an arbitrary viscous stress tensor) and the continuity equation (namely, multiplying the mass conservation law by half the square of the velocity, the momentum conservation law by the velocity, adding them together and subtracting total of the equation for total energy), we get rid of the addends with kinetic energy:
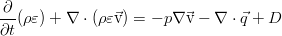
Here a dissipative function arises, equal to the double convolution of the viscous stress tensor and the tensor, which is conventionally sometimes called the velocity gradient:
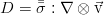
Applying here the mass balance equation and the first law of thermodynamics, in the same way as was done above, we arrive at the entropy balance equation:
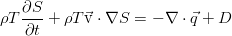
It can be seen that it differs from the equation in an ideal fluid only in the non-zero right-hand side. For an incompressible fluid, we can safely move from entropy to a more tangible value, that is, to temperature, using the definition of heat capacity at constant pressure:
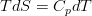
Finally, we can neglect the dissipative function, since it describes the selection due to internal friction, and therefore it is essential only in liquids with very large viscosities, and for the heat flux to use the Fourier thermal conductivity law, which allows expressing it through temperature:
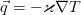
As a result, we obtain the heat conduction equation for an incompressible viscous fluid:
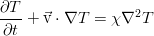
According to it, the temperature of the fluid element changes due to direct convective transport with the fluid flow, as well as due to the quite usual mechanism of molecular heat conduction (right side).
Convection. Boussinesq Approach
Actually, with the description of the convection problem in Habré , this whole hydrodynamic "booth" began. So, we look at a jar with an incompressible viscous liquid, for example, water. Its motion in the case of non-uniform temperature in the volume is described by three equations:
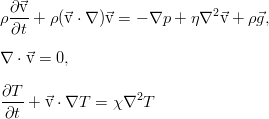
In the general case, this system also includes a state equation relating density, pressure, and temperature. However, then the fluid can no longer be considered incompressible. Practice (and mathematics) shows that with sufficient accuracy one can accept density constant everywhere, except for the term with the force of gravity. Moreover, it suffices to restrict ourselves to linear temperature decomposition:
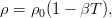
Immediately, we note that there is no longer recorded the absolute temperature, but already a deviation from some "zero" level, at which the density is equal to
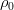. To write this way allows us the equation of heat conduction, since it is linear and is invariant to such shifts. In the term of gravity, it is possible to isolate a part independent of temperature (hydrostatic gradient) and hide it in pressure:
And then we come to the convection equations in the Boussinesq approximation:
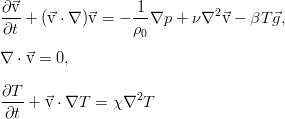
This model is practically common when studying convective phenomena, and on its basis a huge number of very different results were obtained. In particular, in problems of stability of equilibrium of fluid and others.
Tool issue
I digress a little from the topic, although I understand perfectly well that this can only kindle an extra and distracting discussion.
You know what surprised in the comments on the previous post? The fact that readers pay a lot of attention to the question of mathematical rigor of the calculations, which, in general, is not much here. Hydrodynamics was created by Euler and Navier during the rule of French materialism, when the strict results of analytical mechanics, it seemed, described the whole world. But the level of rigor of these results is as it could be at that time, in the barely created by Newton and other differential calculus, and not higher. And so it remains to this day, and the mathematical rigor of hydrodynamics is the same. In practice, this is the last classical field of science, which still has unsolved fundamental problems. Maybe they are not solved precisely because they are formulated in the old, not very developed and not rich in significant means language. I remember that there are some developments in mathematics, where the apparatus is applied to the Navier-Stokes equations, remember the Bipinorov and Dirac gamma-matrices (the basis of quantum field theory), or worse, at night, or even worse. But they are still separate and virtually unknown.
Personally, I assume that the development of the apparatus for solving the Navier-Stokes equations has simply not yet taken place. As is known, these equations perfectly describe both ordered laminar flows and chaos of turbulence. And in the equations for this just enough to change one control parameter. As in nonlinear systems (a-la Lorentz system ), which also have no common analytical solutions, and, in general, a specific detailed analysis of the properties of solutions precisely as mathematical functions. Much at the level of behavior - there is chaos, there is ordering, there is synchronization, there is the influence of the parameter, and the transition, apparently, happens like this. But there is no question about the smoothness of the solutions, nor about their existence in such problems, unlike Navier-Stokes. After all, we still hardly know whether their general smooth solutions exist at all.
Having seen things like “nabla is a 1-form” in the comments, at first I was seriously thinking about whether I had missed something in my education. Yes, about the various kinds of n-forms I mentioned in the courses (but not more) in one semester special course called group theory in physics, from which, however, a lot was not possible because of the absence of a serious structured presentation. But to argue about whether Nabla is a vector or not, it never happens. In physics, which does not deal with significantly mathematized level problems, say, the general theory of relativity and the inherently necessary differential geometry for it, nabla has always been practically a vector. Of course, not quite ordinary, not commuting with them and possessing a number of other properties. Simple, in general, even an ordinary operator, which shows which component of the vector and how we will differentiate. It's just a tool that we can use within the specified limits and we realize that we need to check its suitability when going beyond the boundary of a familiar area, even, for example, when moving from Cartesian coordinates to the same spherical ones.
Sometimes you can spend too much time understanding the hammer, but never really learn how to hammer nails into them. For example, why it has such a shape, why different hammers have a different shape, and then start digging deeper - why metal glitters and wooden handle doesn’t, etc. But the essence of the most frequent use of a hammer will not change from this understanding. They will hammer nails, level the metal on the mandrel, etc. - they will still be knocked, preferably not on the fingers.
At this level is my personal acquaintance with the apparatus of quantum electrodynamics. By the principle - I remember, something passed. Moreover, even the training manual was published from a distance with a teacher of this subject last year, but somehow it is still aside - I am not doing it.
Further
The next post will be devoted to problems of stability for equilibrium and stationary flow. There once again we will see that even the simplest problems of hydrodynamics cannot be solved analytically in full form, and therefore we have to apply many different, at first glance, very controversial, but at the same time perfectly working and sound methods. I hope that we can already move from abstract to more tangible things.
Source: https://habr.com/ru/post/176157/
All Articles