Blind Deconvolution - automatic recovery of blurred images
Blurred images - one of the most unpleasant defects in photography, along with defocused images. Earlier, I wrote about deconvolution algorithms for reconstructing blurred and defocused images. These relatively simple approaches allow you to restore the original image, if you know the exact trajectory of blurring (or the shape of the blur spot).
In most cases, the blur trajectory is assumed to be a straight line, the parameters of which should be set by the user himself - this requires a fairly painstaking work on the selection of the core, and in real photographs the blur trajectory is far from the line and represents an intricate variable density / brightness curve, the shape of which is extremely hard to pick by hand.

In the past few years, a new direction in image restoration theory has been intensively developing - blind reverse convolution (Blind Deconvolution). There was a lot of work on this topic, and the active commercial use of the results begins.
Many of you remember the Adobe MAX 2011 conference, at which they just showed how one of the Blind Deconvolution algorithms works: Fix blurred photos in a new version of Photoshop
In this article I want to tell you more about how this amazing technology works, and also to show the practical implementation of SmartDeblur, which now also has this algorithm at its disposal.
Attention, under the cut a lot of pictures!
Part 1. Theory - Restoring defocused and blurred images
Part 2. Practice - Restoring defocused and blurred images
Part 3. Improving quality - Restoring defocused and blurred images
It is recommended that you read at least the first theoretical part in order to better understand what convolution, deconvolution, Fourier transform, and other terms are. Although I promised that the third part will be the last, but I could not resist telling you about the latest trends in the field of image restoration.
I will look at Blind Decovolution on the example of the work of American Professor Rob Fergus “Removing the Camera Shake from a Single Photograph”. The original article can be found on his page: http://cs.nyu.edu/~fergus/pmwiki/pmwiki.php
This is not the newest work, there have recently appeared many other publications that demonstrate the best results - but they use quite complex mathematics ((for an unprepared reader) in a number of stages, and the basic principle remains the same. In addition, Fergus’s work is his kind of "classics", he was one of the first to propose a fundamentally new approach that allowed the automatic determination of the lubrication core even for very complex cases.
')
Take a camera and take a blurred picture - the benefit for this does not require much effort :)

We introduce the following notation:
B - observed blurred image
K - blur core (blur path), kernel
L - the original non-blurred image (hidden)
N - additive noise
Then the process of blurring / distortion can be described as the following expression
B = K * L + N
Where the symbol "*" is a convolution operation, not to be confused with ordinary multiplication!
What is convolution, you can read in the first part
In a visual form, this can be represented as follows (omitting the noise component for simplicity):

So what is the most difficult?
Imagine a simple analogy - the number 11 consists of two factors. What are they?
The solutions are infinite:
11 = 1 x 11
11 = 2 x 5.5
11 = 3 x 3.667
etc.
Or, moving to a visual representation:

Those. need more information. One of the variants of this is setting the target function - this is such a function, the value of which is the higher (in the simple case), the closer the result is to the desired one.
Studies have shown that despite the fact that real images have a large scatter of values of individual pixels, the gradients of these values have the form of a distribution with slowly decreasing boundaries ( Heavy-tailed distribution ). Such a distribution has a peak in the vicinity of zero and, unlike the Gaussian distribution, has much higher probabilities of large values (here is such an oil).
This coincides with the intuitive view that in real images in most cases there are large areas of more or less constant brightness, which end with objects with sharp and medium brightness differences.
Here is an example of a gradient histogram for a sharp image:

And for a blurred image:

Thus, we obtained a tool that allows us to measure the "quality" of the result obtained in terms of clarity and similarity to the real image.
Now we can formulate the main points for the construction of the completed model:
1. Restrictions imposed by the distortion model B = K * L + N
2. The objective function for the reconstruction result is how similar the gradient histogram is to the theoretical distribution with slowly decreasing boundaries. Denote it as p (L P )
3. The objective function for the distortion core is positive values and a low proportion of white pixels (since the blur trajectory is usually represented by a thin line). Denote it as p (K)
Combine all this into a common objective function as follows:
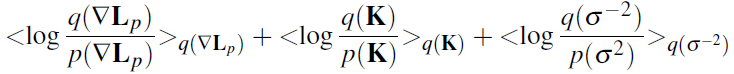
Where q (L P ) , q (K) distributions obtained by the Variational Bayesian approach
Further, this objective function is minimized by the method of coordinate descent with some additions, which I will not describe because of their complexity and the abundance of formulas - all this can be read in the work of Fergus.
This approach allows to improve the quality of the existing core, but they cannot build this core from scratch, because most likely in the process of finding a solution, we will fall into one of the local minima.
First, from the input blurred image, we build a pyramid of images with different resolutions. From the smallest size to the original size.
Next, we initialize the algorithm using a 3 * 3 kernel with one of the simple patterns — a vertical line, a horizontal line, or a Gaussian spot. As a universal option, you can choose the last - Gaussian spot.
Using the optimization algorithm described above, we improve the kernel estimate using the smallest image size in the constructed pyramid.
After that, we resize the resulting updated core to, say, 5 * 5 pixels and repeat the process already with the image of the next size.
Thus, at each step, we slightly improve the core and as a result we obtain a very accurate trajectory of blurring.
Let us demonstrate an iterative construction of the kernel using an example.
Source Image:

Kernel refinement process:

The first and third lines show the core score at each level of the image pyramid.
The second and fourth lines are the evaluation of the undistorted image.
Result:


More modern approaches have approximately the idea of consistently refining the core, but using more sophisticated variants of the objective function for the result of the reconstruction and the core distortion. In addition, intermediate and final filtering of the obtained core is carried out in order to remove the extra noise and correct some errors in the refinement algorithm.
We implemented a similar option and added a new feature to SmartDeblur 2.0 - everything is still free :)
Project address: smartdeblur.net
(Sources and binaries from the previous version can be found on GitHub: github.com/Y-Vladimir/SmartDeblur )
Work example:

Another example:
And finally, the result of the work on the image from the Adobe MAX 2011 conference:
As you can see, the result is almost perfect - almost like Adobe shows them.
Later we will increase it after we optimize the deconvolution and the pyramidal construction.
The interface is as follows:
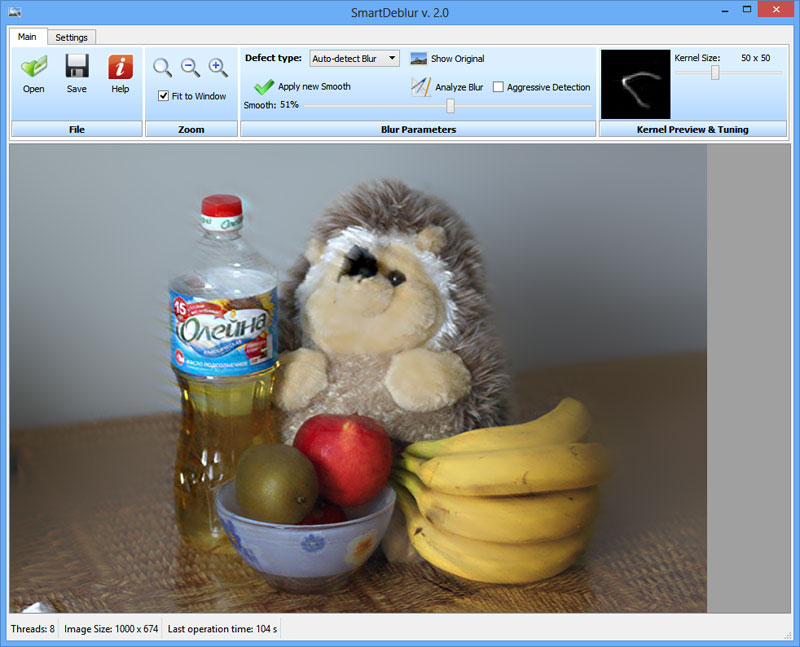
To work with the program, you only need to upload an image and click on "Analyze Blur" and agree with the choice of the entire image - the analysis may take several minutes. If the result does not suit you, you can select a different region (select the mouse on the image by moving it to the right and down, a little not obvious, but so far :)). The right button selection is removed.
The “Agressive Detection” checkbox changes the parameters to select only the most important elements of the core.
So far, good results are achieved far from all the images - so we will be very happy with feedback, this will help us improve the algorithms!
Vladimir Yuzhikov (Vladimir Yuzhikov)
In most cases, the blur trajectory is assumed to be a straight line, the parameters of which should be set by the user himself - this requires a fairly painstaking work on the selection of the core, and in real photographs the blur trajectory is far from the line and represents an intricate variable density / brightness curve, the shape of which is extremely hard to pick by hand.

In the past few years, a new direction in image restoration theory has been intensively developing - blind reverse convolution (Blind Deconvolution). There was a lot of work on this topic, and the active commercial use of the results begins.
Many of you remember the Adobe MAX 2011 conference, at which they just showed how one of the Blind Deconvolution algorithms works: Fix blurred photos in a new version of Photoshop
In this article I want to tell you more about how this amazing technology works, and also to show the practical implementation of SmartDeblur, which now also has this algorithm at its disposal.
Attention, under the cut a lot of pictures!
Start
This post is a continuation of a series of my posts "Restoring defocused and blurred images":Part 1. Theory - Restoring defocused and blurred images
Part 2. Practice - Restoring defocused and blurred images
Part 3. Improving quality - Restoring defocused and blurred images
It is recommended that you read at least the first theoretical part in order to better understand what convolution, deconvolution, Fourier transform, and other terms are. Although I promised that the third part will be the last, but I could not resist telling you about the latest trends in the field of image restoration.
I will look at Blind Decovolution on the example of the work of American Professor Rob Fergus “Removing the Camera Shake from a Single Photograph”. The original article can be found on his page: http://cs.nyu.edu/~fergus/pmwiki/pmwiki.php
This is not the newest work, there have recently appeared many other publications that demonstrate the best results - but they use quite complex mathematics ((for an unprepared reader) in a number of stages, and the basic principle remains the same. In addition, Fergus’s work is his kind of "classics", he was one of the first to propose a fundamentally new approach that allowed the automatic determination of the lubrication core even for very complex cases.
')
Distortion model
And so, let's get started.Take a camera and take a blurred picture - the benefit for this does not require much effort :)

We introduce the following notation:
B - observed blurred image
K - blur core (blur path), kernel
L - the original non-blurred image (hidden)
N - additive noise
Then the process of blurring / distortion can be described as the following expression
B = K * L + N
Where the symbol "*" is a convolution operation, not to be confused with ordinary multiplication!
What is convolution, you can read in the first part
In a visual form, this can be represented as follows (omitting the noise component for simplicity):

So what is the most difficult?
Imagine a simple analogy - the number 11 consists of two factors. What are they?
The solutions are infinite:
11 = 1 x 11
11 = 2 x 5.5
11 = 3 x 3.667
etc.
Or, moving to a visual representation:

Objective function
To get a specific solution, you need to impose restrictions, to somehow describe the model of what we are striving for.Those. need more information. One of the variants of this is setting the target function - this is such a function, the value of which is the higher (in the simple case), the closer the result is to the desired one.
Studies have shown that despite the fact that real images have a large scatter of values of individual pixels, the gradients of these values have the form of a distribution with slowly decreasing boundaries ( Heavy-tailed distribution ). Such a distribution has a peak in the vicinity of zero and, unlike the Gaussian distribution, has much higher probabilities of large values (here is such an oil).
This coincides with the intuitive view that in real images in most cases there are large areas of more or less constant brightness, which end with objects with sharp and medium brightness differences.
Here is an example of a gradient histogram for a sharp image:

And for a blurred image:

Thus, we obtained a tool that allows us to measure the "quality" of the result obtained in terms of clarity and similarity to the real image.
Now we can formulate the main points for the construction of the completed model:
1. Restrictions imposed by the distortion model B = K * L + N
2. The objective function for the reconstruction result is how similar the gradient histogram is to the theoretical distribution with slowly decreasing boundaries. Denote it as p (L P )
3. The objective function for the distortion core is positive values and a low proportion of white pixels (since the blur trajectory is usually represented by a thin line). Denote it as p (K)
Combine all this into a common objective function as follows:
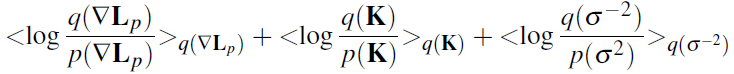
Where q (L P ) , q (K) distributions obtained by the Variational Bayesian approach
Further, this objective function is minimized by the method of coordinate descent with some additions, which I will not describe because of their complexity and the abundance of formulas - all this can be read in the work of Fergus.
This approach allows to improve the quality of the existing core, but they cannot build this core from scratch, because most likely in the process of finding a solution, we will fall into one of the local minima.
Pyramidal approach
The solution to this problem is an iterative approach to the construction of the core distortion.First, from the input blurred image, we build a pyramid of images with different resolutions. From the smallest size to the original size.
Next, we initialize the algorithm using a 3 * 3 kernel with one of the simple patterns — a vertical line, a horizontal line, or a Gaussian spot. As a universal option, you can choose the last - Gaussian spot.
Using the optimization algorithm described above, we improve the kernel estimate using the smallest image size in the constructed pyramid.
After that, we resize the resulting updated core to, say, 5 * 5 pixels and repeat the process already with the image of the next size.
Thus, at each step, we slightly improve the core and as a result we obtain a very accurate trajectory of blurring.
Let us demonstrate an iterative construction of the kernel using an example.
Source Image:

Kernel refinement process:

The first and third lines show the core score at each level of the image pyramid.
The second and fourth lines are the evaluation of the undistorted image.
Result:

Flowchart
It remains to put everything together and describe the entire algorithm:
More modern approaches have approximately the idea of consistently refining the core, but using more sophisticated variants of the objective function for the result of the reconstruction and the core distortion. In addition, intermediate and final filtering of the obtained core is carried out in order to remove the extra noise and correct some errors in the refinement algorithm.
Practical implementation
Probably the most interesting thing is to play with the Blind Deconvolution algorithm live on real images!We implemented a similar option and added a new feature to SmartDeblur 2.0 - everything is still free :)
Project address: smartdeblur.net
(Sources and binaries from the previous version can be found on GitHub: github.com/Y-Vladimir/SmartDeblur )
Work example:

Another example:
 |  |
 |
And finally, the result of the work on the image from the Adobe MAX 2011 conference:
 |  |
 |
As you can see, the result is almost perfect - almost like Adobe shows them.
Technical details
So far, the maximum size of the processed image is set to 1200 * 1200. This is due to the fact that the algorithms consume a lot of memory. Even in the image of 1000 pixels - more gigabytes. Therefore, a size limit has been introduced.Later we will increase it after we optimize the deconvolution and the pyramidal construction.
The interface is as follows:

To work with the program, you only need to upload an image and click on "Analyze Blur" and agree with the choice of the entire image - the analysis may take several minutes. If the result does not suit you, you can select a different region (select the mouse on the image by moving it to the right and down, a little not obvious, but so far :)). The right button selection is removed.
The “Agressive Detection” checkbox changes the parameters to select only the most important elements of the core.
So far, good results are achieved far from all the images - so we will be very happy with feedback, this will help us improve the algorithms!
--Vladimir Yuzhikov (Vladimir Yuzhikov)
Source: https://habr.com/ru/post/175717/
All Articles