Theoretical computer science at the Academic University
I want to describe the story of one arrogant and narcissistic student of the Academic University, whom I, of course, am not, but I can well imagine his thoughts and experiences. We will call this student, for example, Shurik. At the time Shurik entered the Academic University (AU), according to his programmer resume, he was already an expert in the field of algorithms. He masterfully mastered the depth-first search algorithm, knew several methods for sorting arrays, and had an idea about the binary search. Naturally, the course of algorithms did not interest him completely, and indeed, there is little that can be taught to a programmer with five years of experience. He was interested in the program of theoretical computer science AU because there were too many words unknown to him in the topics on subjects he knew. But this is Peter, where they and the curb are sometimes called a strange word, and they probably pondered for searching in depth beautiful words. He carefully studied the slides and videos of courses. It turned out that there is some kind of computer science out there, which Shurik does not speak perfectly. Shurik collected books, socks and five years of experience, and went to St. Petersburg for an interview. There he met people who could even teach a programmer with such experience. It all ruined Shurikov's picture of the world, in which knowledge of computer science was measured by the number of written classes in C #.
During his master's degree studies, Shurik was engaged in research in the field of circuit complexity and the field of exponential algorithms. It is really very interesting and, equally important, it is useful for admission to graduate school.
At the moment, Shurik is a happy graduate student at New York University, uses the word "curb", and recalls with deep gratitude the Academic University . And the department of mathematical and information technologies of the AU is still leading a set of new undergraduates, in particular, in the direction of “theoretical informatics”.
Now I give the floor to Shurik, who will talk about one of his research.
NP-hard problems are problems that are often encountered in practice, for which effective solution algorithms are unknown. The study of such problems is of great interest, since the existence of an efficient algorithm for any of these problems implies the existence of efficient algorithms for all problems of class NP. Conversely, if we can prove that at least for one of these tasks there is no effective algorithm, then this will mean that there are no such algorithms for all NP-hard problems. In the master of AU, we investigated exact and approximate algorithms for solving some NP-hard problems. For example, we managed to obtain new algorithms for solving the problem of maximal feasibility, the traveling salesman problem, and the shortest common superstructure problem. Next, I want to describe one of these algorithms, namely, an algorithm for the approximate solution of the traveling salesman problem.

The NP-difficult optimization problem is an NP-difficult problem, in which among all possible solutions you need to choose the optimal in some sense solution. For example, find the shortest cycle that passes through each vertex of a given weighted graph exactly once. Perhaps there are many ways to get around the graph, passing on each vertex exactly once, but we are interested only in those detours that are minimal in weight. This task is called the traveling salesman problem. The running time of the best known algorithms for this problem is at worst approximately equal to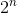 . We were engaged in the acceleration of algorithms for problems of this kind. For example, an algorithm that works for
. We were engaged in the acceleration of algorithms for problems of this kind. For example, an algorithm that works for 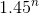 , will allow to solve the problem for large values of n. It is interesting to note that buying a computer that works 1000 times faster will not give such acceleration as a new algorithm with a smaller exponent in runtime. The existence of a polynomial algorithm for this problem implies the equality of the classes P and NP, and the proof of the absence of such an algorithm would mean that these classes are not equal.
, will allow to solve the problem for large values of n. It is interesting to note that buying a computer that works 1000 times faster will not give such acceleration as a new algorithm with a smaller exponent in runtime. The existence of a polynomial algorithm for this problem implies the equality of the classes P and NP, and the proof of the absence of such an algorithm would mean that these classes are not equal.
A Hamiltonian cycle of a graph is a cycle that passes through each vertex of the graph exactly once. The traveling salesman problem (traveling salesman problem, TSP ) is to find the Hamiltonian cycle of minimum weight in a given weighted graph. Denote by n the number of vertices of the original graph, and by M the maximum weight of the edge. There are many methods for solving the traveling salesman problem in practice, but in this article we will only talk about theoretical algorithms with provable estimates for the operating time in the worst case.
')
In 1962, a dynamic programming algorithm was developed that resolves the TSP over time.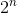 but using exponential
but using exponential 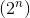 memory. The best known algorithm using only polynomial memory has a running time.
memory. The best known algorithm using only polynomial memory has a running time. 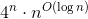 . Intermediate results are also known, for example, for any
. Intermediate results are also known, for example, for any 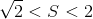 , there is an algorithm for solving the problem with the time of work
, there is an algorithm for solving the problem with the time of work 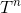 using memory
using memory 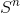 where
where 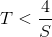 . There are known algorithms based on the inclusion-exclusion formula that solve the problem in time.
. There are known algorithms based on the inclusion-exclusion formula that solve the problem in time. 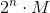 using memory
using memory 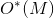 .
. 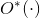 hides polynomial factors from the entry length, i.e.
hides polynomial factors from the entry length, i.e. 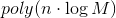 . For an undirected TSP case, there is a Monte-Carlo algorithm with running time
. For an undirected TSP case, there is a Monte-Carlo algorithm with running time 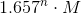 and an exponentially small probability of error.
and an exponentially small probability of error.
For more than fifty years, the following questions have been open:
It is known that under the assumption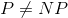 The total TSP cannot be approximated with any polynomially computable factor. That is, in this assumption, it is impossible to find not only the 10-approximation of the optimal solution, but even the n! -Approach. A particular case in which the weights of the edges of the graph satisfy the triangle inequality is called the metric traveling salesman problem . For the undirected metric problem, the 1.5 approximation is known. Even for this particular case, it is known that under the assumption
The total TSP cannot be approximated with any polynomially computable factor. That is, in this assumption, it is impossible to find not only the 10-approximation of the optimal solution, but even the n! -Approach. A particular case in which the weights of the edges of the graph satisfy the triangle inequality is called the metric traveling salesman problem . For the undirected metric problem, the 1.5 approximation is known. Even for this particular case, it is known that under the assumption 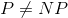 , it is impossible to find a polynomial algorithm with better approximation
, it is impossible to find a polynomial algorithm with better approximation 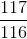 (in the oriented case -
(in the oriented case - 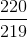 ). For the oriented metric version of the problem, the approximation factor was recently improved to
). For the oriented metric version of the problem, the approximation factor was recently improved to 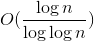 .
.
We propose an algorithm that for any fixed uses
uses 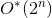 steps and polynomial memory to calculate
steps and polynomial memory to calculate 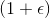 -approach of the oriented metric traveling salesman problem. As mentioned above, the best known polynomial approximation even for the unoriented metric version of the TSP is 1.5 (for the oriented -
-approach of the oriented metric traveling salesman problem. As mentioned above, the best known polynomial approximation even for the unoriented metric version of the TSP is 1.5 (for the oriented - 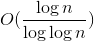 ).
).
If a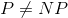 , then in polynomial time can not be found
, then in polynomial time can not be found 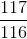 -approach unoriented metric TSP.
-approach unoriented metric TSP.
If we need, for example,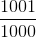 -approach, then we must use exact algorithms that require either exponential memory or time
-approach, then we must use exact algorithms that require either exponential memory or time 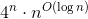 . Exponential algorithms are rarely used in practice, but in any case, we are able to run them and wait for a response. However, if the algorithm uses exponential memory, then we cannot even run the algorithm on inputs of a reasonable size.
. Exponential algorithms are rarely used in practice, but in any case, we are able to run them and wait for a response. However, if the algorithm uses exponential memory, then we cannot even run the algorithm on inputs of a reasonable size.
The proposed algorithm can find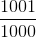 -approach total tsp over time
-approach total tsp over time 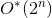 using only polynomial memory.
using only polynomial memory.
The developed algorithm uses the idea proposed for constructing a completely polynomial approximate scheme for the backpack problem in the work of Ibarra, Kim . The authors use a pseudopolynomial algorithm for the backpack problem, which works over time.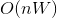 where n is the number of items, and W is the capacity of the backpack.
where n is the number of items, and W is the capacity of the backpack.
Fully polynomial approximation of the backpack problem first divides the weights of all items by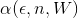 , then calls the pseudopolynomial algorithm. The resulting answer may not be optimal, because some weights are not just divided into
, then calls the pseudopolynomial algorithm. The resulting answer may not be optimal, because some weights are not just divided into 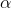 but also rounded. However, a simple analysis shows that rounding does not greatly affect the result.
but also rounded. However, a simple analysis shows that rounding does not greatly affect the result.
We use a similar idea. Through OPT we denote the optimal solution TSP. In order to obtain an approximate algorithm that is polynomial in memory, we first divide the weights of all edges by a sufficiently large number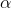 , then run the exact algorithm based on the inclusion-exception formula. The running time of the resulting algorithm will be equal to
, then run the exact algorithm based on the inclusion-exception formula. The running time of the resulting algorithm will be equal to 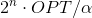 and the length of the resulting cycle will be no more
and the length of the resulting cycle will be no more 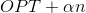 . Now we want to choose
. Now we want to choose 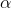 so that
so that 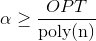 and
and 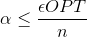 . The metric version of TSP can be approximated in polynomial time, for example, with the factor
. The metric version of TSP can be approximated in polynomial time, for example, with the factor 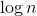 . That is, we can find
. That is, we can find 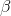 , what
, what 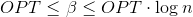 and take
and take 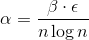 . Then the resulting algorithm will have a running time.
. Then the resulting algorithm will have a running time. 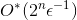 and use memory
and use memory 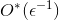 . We also managed to generalize this result for the case of the general (non-metric oriented) traveling salesman problem.
. We also managed to generalize this result for the case of the general (non-metric oriented) traveling salesman problem.
During his master's degree studies, Shurik was engaged in research in the field of circuit complexity and the field of exponential algorithms. It is really very interesting and, equally important, it is useful for admission to graduate school.
At the moment, Shurik is a happy graduate student at New York University, uses the word "curb", and recalls with deep gratitude the Academic University . And the department of mathematical and information technologies of the AU is still leading a set of new undergraduates, in particular, in the direction of “theoretical informatics”.
Now I give the floor to Shurik, who will talk about one of his research.
Algorithms for NP-hard problems
NP-hard problems are problems that are often encountered in practice, for which effective solution algorithms are unknown. The study of such problems is of great interest, since the existence of an efficient algorithm for any of these problems implies the existence of efficient algorithms for all problems of class NP. Conversely, if we can prove that at least for one of these tasks there is no effective algorithm, then this will mean that there are no such algorithms for all NP-hard problems. In the master of AU, we investigated exact and approximate algorithms for solving some NP-hard problems. For example, we managed to obtain new algorithms for solving the problem of maximal feasibility, the traveling salesman problem, and the shortest common superstructure problem. Next, I want to describe one of these algorithms, namely, an algorithm for the approximate solution of the traveling salesman problem.

The NP-difficult optimization problem is an NP-difficult problem, in which among all possible solutions you need to choose the optimal in some sense solution. For example, find the shortest cycle that passes through each vertex of a given weighted graph exactly once. Perhaps there are many ways to get around the graph, passing on each vertex exactly once, but we are interested only in those detours that are minimal in weight. This task is called the traveling salesman problem. The running time of the best known algorithms for this problem is at worst approximately equal to
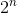 . We were engaged in the acceleration of algorithms for problems of this kind. For example, an algorithm that works for
. We were engaged in the acceleration of algorithms for problems of this kind. For example, an algorithm that works for 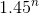 , will allow to solve the problem for large values of n. It is interesting to note that buying a computer that works 1000 times faster will not give such acceleration as a new algorithm with a smaller exponent in runtime. The existence of a polynomial algorithm for this problem implies the equality of the classes P and NP, and the proof of the absence of such an algorithm would mean that these classes are not equal.
, will allow to solve the problem for large values of n. It is interesting to note that buying a computer that works 1000 times faster will not give such acceleration as a new algorithm with a smaller exponent in runtime. The existence of a polynomial algorithm for this problem implies the equality of the classes P and NP, and the proof of the absence of such an algorithm would mean that these classes are not equal.Traveling salesman task
A Hamiltonian cycle of a graph is a cycle that passes through each vertex of the graph exactly once. The traveling salesman problem (traveling salesman problem, TSP ) is to find the Hamiltonian cycle of minimum weight in a given weighted graph. Denote by n the number of vertices of the original graph, and by M the maximum weight of the edge. There are many methods for solving the traveling salesman problem in practice, but in this article we will only talk about theoretical algorithms with provable estimates for the operating time in the worst case.

')
Exact algorithms for solving the traveling salesman problem
In 1962, a dynamic programming algorithm was developed that resolves the TSP over time.
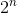 but using exponential
but using exponential 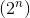 memory. The best known algorithm using only polynomial memory has a running time.
memory. The best known algorithm using only polynomial memory has a running time. 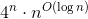 . Intermediate results are also known, for example, for any
. Intermediate results are also known, for example, for any 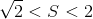 , there is an algorithm for solving the problem with the time of work
, there is an algorithm for solving the problem with the time of work 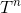 using memory
using memory 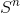 where
where 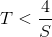 . There are known algorithms based on the inclusion-exclusion formula that solve the problem in time.
. There are known algorithms based on the inclusion-exclusion formula that solve the problem in time. 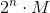 using memory
using memory 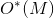 .
. 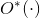 hides polynomial factors from the entry length, i.e.
hides polynomial factors from the entry length, i.e. 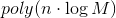 . For an undirected TSP case, there is a Monte-Carlo algorithm with running time
. For an undirected TSP case, there is a Monte-Carlo algorithm with running time 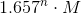 and an exponentially small probability of error.
and an exponentially small probability of error.For more than fifty years, the following questions have been open:
- Existence of an algorithm for a TSP with running time
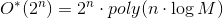 and polynomial memory.
and polynomial memory. - Existence of an algorithm for a TSP with running time
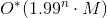 for the general (oriented) case of the traveling salesman problem.
for the general (oriented) case of the traveling salesman problem.
Approximate algorithms for solving the traveling salesman problem
It is known that under the assumption
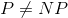 The total TSP cannot be approximated with any polynomially computable factor. That is, in this assumption, it is impossible to find not only the 10-approximation of the optimal solution, but even the n! -Approach. A particular case in which the weights of the edges of the graph satisfy the triangle inequality is called the metric traveling salesman problem . For the undirected metric problem, the 1.5 approximation is known. Even for this particular case, it is known that under the assumption
The total TSP cannot be approximated with any polynomially computable factor. That is, in this assumption, it is impossible to find not only the 10-approximation of the optimal solution, but even the n! -Approach. A particular case in which the weights of the edges of the graph satisfy the triangle inequality is called the metric traveling salesman problem . For the undirected metric problem, the 1.5 approximation is known. Even for this particular case, it is known that under the assumption 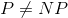 , it is impossible to find a polynomial algorithm with better approximation
, it is impossible to find a polynomial algorithm with better approximation 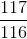 (in the oriented case -
(in the oriented case - 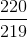 ). For the oriented metric version of the problem, the approximation factor was recently improved to
). For the oriented metric version of the problem, the approximation factor was recently improved to 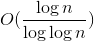 .
.Approximation in exponential time
We propose an algorithm that for any fixed
 uses
uses 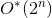 steps and polynomial memory to calculate
steps and polynomial memory to calculate 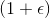 -approach of the oriented metric traveling salesman problem. As mentioned above, the best known polynomial approximation even for the unoriented metric version of the TSP is 1.5 (for the oriented -
-approach of the oriented metric traveling salesman problem. As mentioned above, the best known polynomial approximation even for the unoriented metric version of the TSP is 1.5 (for the oriented - 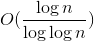 ).
).If a
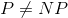 , then in polynomial time can not be found
, then in polynomial time can not be found 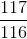 -approach unoriented metric TSP.
-approach unoriented metric TSP.If we need, for example,
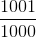 -approach, then we must use exact algorithms that require either exponential memory or time
-approach, then we must use exact algorithms that require either exponential memory or time 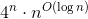 . Exponential algorithms are rarely used in practice, but in any case, we are able to run them and wait for a response. However, if the algorithm uses exponential memory, then we cannot even run the algorithm on inputs of a reasonable size.
. Exponential algorithms are rarely used in practice, but in any case, we are able to run them and wait for a response. However, if the algorithm uses exponential memory, then we cannot even run the algorithm on inputs of a reasonable size.The proposed algorithm can find
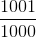 -approach total tsp over time
-approach total tsp over time 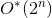 using only polynomial memory.
using only polynomial memory.The developed algorithm uses the idea proposed for constructing a completely polynomial approximate scheme for the backpack problem in the work of Ibarra, Kim . The authors use a pseudopolynomial algorithm for the backpack problem, which works over time.
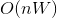 where n is the number of items, and W is the capacity of the backpack.
where n is the number of items, and W is the capacity of the backpack.Fully polynomial approximation of the backpack problem first divides the weights of all items by
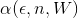 , then calls the pseudopolynomial algorithm. The resulting answer may not be optimal, because some weights are not just divided into
, then calls the pseudopolynomial algorithm. The resulting answer may not be optimal, because some weights are not just divided into 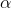 but also rounded. However, a simple analysis shows that rounding does not greatly affect the result.
but also rounded. However, a simple analysis shows that rounding does not greatly affect the result.We use a similar idea. Through OPT we denote the optimal solution TSP. In order to obtain an approximate algorithm that is polynomial in memory, we first divide the weights of all edges by a sufficiently large number
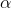 , then run the exact algorithm based on the inclusion-exception formula. The running time of the resulting algorithm will be equal to
, then run the exact algorithm based on the inclusion-exception formula. The running time of the resulting algorithm will be equal to 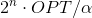 and the length of the resulting cycle will be no more
and the length of the resulting cycle will be no more 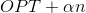 . Now we want to choose
. Now we want to choose 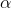 so that
so that 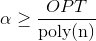 and
and 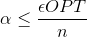 . The metric version of TSP can be approximated in polynomial time, for example, with the factor
. The metric version of TSP can be approximated in polynomial time, for example, with the factor 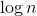 . That is, we can find
. That is, we can find 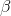 , what
, what 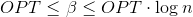 and take
and take 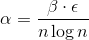 . Then the resulting algorithm will have a running time.
. Then the resulting algorithm will have a running time. 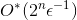 and use memory
and use memory 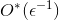 . We also managed to generalize this result for the case of the general (non-metric oriented) traveling salesman problem.
. We also managed to generalize this result for the case of the general (non-metric oriented) traveling salesman problem.Source: https://habr.com/ru/post/175113/
All Articles