Solving the problem of finding the angles of installation of a video camera over the road using different methods in Wolfram Mathematica. Part 1

Formulation of the problem

There is a system located above the roadway, which includes a video camera. Known camcorder resolution and viewing angles. Regarding the roadway, the video camera is installed as follows: from above above any of the lanes, to the side of the roadway no more than 3 meters from the edge of the nearest controlled lane. The number of simultaneously controlled traffic lanes is no more than 4. The video camera takes photographs of the control zone with a certain frame rate. All the frames taken are input to the license plate recognition system. The result of the passage of the vehicle (hereinafter referred to as TC) is a track with the coordinates of the center of the frame of the vehicle license plate in the form:

x11 y11 x12 y12 … x1i y1i … x1n y1n

The result of the passage of several vehicles is a file of tracks in the form:

x11 y11 x12 y12 … x1i y1i … x1n y1n
x21 y21 x22 y22 … x2i y2i … x2n y2n
...
xi1 yi1 xi2 yi2 … xii yii … xin yin
...
xn1 yn1 xn2 yn2 … xni yni … xnn ynn

Sample track file:
')
1420 23 1399 44 1377 62 1351 82
417 327 368 359 313 392 119 500 48 540
2300 62 2291 91 2275 125 2267 159 2254 197
2298 114 2263 223 2199 413 2180 470 2158 532

It is necessary, having a file with the structure described above, to determine the angle of inclination of the video camera relative to the trajectories of vehicles and rotation of the video camera relative to the edge of the shoulder.

Data import

We import data with which we will work.

Our file is located in the directory from which the laptop is launched (Mathematica document), called recdat.txt file. For import, enter:

file = Import[NotebookDirectory[] <> "recdat.txt", "Table"];

file - the variable into which the file is imported
NotebookDirectory[] - returns the directory where the laptop is located as a string
<> - abbreviated notation of a function connecting strings
"recdat.txt" is a string indicating the name of the file with the tracks.
"Table" is an option of the Import [] function indicating that this file must be imported as a table, respectively, the file variable will have the type of a table (list)
Symbol ; at the end of the line says that Mathematica will not display the result of the execution of the described function after its execution.
Pressing Shift + Enter will import our file.

To see how the data was imported, you must enter file and press Shift + Enter, but for a more visual display of information, we will use the following function:

TableForm[file]

1420 23 1399 44 1377 62 1351 82
417 327 368 359 313 392 119 500 48 540
2300 62 2291 91 2275 125 2267 159 2254 197
2298 114 2263 223 2199 413 2180 470 2158 532

TableForm[list] - performs output with list elements located in an array of rectangular elements

We determine the constants that define the resolution of the video camera and the viewing angles:

Xlen = 2360; (* *)
Ylen = 1776; (* *)
Xang = 14; (* *)
Yang = Xang*3/4; (* *)

Determine the number of tracks in the file:

length = Length[file];

Length[list] - returns the number of elements of a one-dimensional list or the number of dimensions in the case of a multi-dimensional list

Expanding imported data into structure

The imported data is a structure that is inconvenient to work in Mathematica. It will be much more convenient to work with them if you decompose them into a structure in the form of a three-dimensional list, where the element with index i, j consists of two elements - the x- and y-coordinates of the center of the plate, while i is the serial number of the plate, and j - the sequence number of the track point for the i-th license plate.

A small digression from the topic:

In Mathematica, the same action can be done in different ways, because Wednesday includes a huge set of different functions; one and the same action can be done with the help of a cycle, and it is possible using the special function Mathematica. As a rule, the execution time of an action aimed at one and the same functionality is less when it is performed using the standard Wolfram function, rather than when it is performed using a handwritten loop. Timing[] function helps determine the execution time of a function or set of functions.

To create a list in which we decompose the structure, first declare the variable as a list:

num = {};

To lay out our data structure, we write a loop:

Do[num = Append[num,
Partition[file[[i]], 2]],
{i, length}]

Do [action, {loop condition}]
Append[list,element] - appends the element to the end of the list
Partition[list,n] - splits the list into non-overlapping parts with length n. If the number of elements in the list is not completely divided by n, then the last k (k <n) elements are deleted.
file[[i]] - returns i list item

Now let us turn to the function already familiar to us, and see what the structure looks like that is convenient for further processing:

TableForm[num, TableSpacing -> {3, 4}]



TableSpacing -> {3, 4} - sets indents between list items when displaying

Getting track equations

In the particular case of the track point must be linearized. “In private” because the data considered above was obtained on a straight road where vehicles move at high speeds and during the passage of the control zone, physically at such speed they cannot move along paths that are very different from straight lines.

Equations of motion of the vehicle we will write in the list. To do this, we first declare it:

numeq = {};

And write a function to determine the equations of motion of the vehicle through the control zone. Here it is necessary to say that the origin of coordinates in the frame is the upper left corner of the frame, so:

Do[numeq = Append[numeq,
Fit[num[[i]], {1, x}, x]],
{i, length}]

Fit [data, funs, vars] - for the data list, data searches for the least squares approximation in the form of a linear combination of funs functions of vars variables. Data data can have the form {{x1, y1, ..., f1}, {x2, y2, ..., f2}, ...}, where the number of coordinates x, y, ... is equal to the number of variables in the vars list . Also, data data can be represented in the form {f1, f2, ...} with one coordinate, which takes values ​​1,2, ... Argument funs can be any list of functions that depend only on vars objects.

In our case, for each i-th element of the multidimensional num list containing a two-dimensional array of points — the TS license plate centers — we determine, using the least squares method, the function of the form kx + b closest to the existing set of points.

The result of the execution of this cycle is a list, which roughly consists of the following:

{1167.11 - 0.803101 x, 568.193 - 0.571513 x, 6110.1 - 2.62293 x, 6471.36 - 2.75496 x, 1199.09 - 0.812067 x, 2491.96 - 1.29425 x, 1121.33 - 0.787616 x, 2933.43 - 1.75218 x, 625.959 - 0.609492 x, 2512.3 - 1.30408 x, 7805.9 - 3.3897 x, 881.413 - 0.698268 x, 2651.99 - 1.3463 x, 6140.19 - 2.61239 x, 2594.17 - 1.27645 x, 557.83 - 0.587095 x, 1195.29 - 0.82697 x, 6346.13 - 2.73884 x, 6887.01 - 2.92561 x, 2377.62 - 1.26743 x, 3241.53 - 1.72441 x, 1424.49 - 0.846298 x, 1218.75 - 0.83174 x, 7203.35 - 3.089 x, 5420.94 - 2.28441 x, 2500.74 - 1.29295 x, 2402.61 - 1.25934 x, 6760. - 2.89566 x, 1175.7 - 0.794353 x, 1117.2 - 0.77705 x, 7066.9 - 3.00537 x, 2346.99 - 1.24765 x, 2698.98 - 1.39178 x, 1277.43 - 0.849703 x, 633.372 - 0.61772 x, 2578.56 - 1.3082 x, 2952.21 - 1.47007 x, 1107.8 - 0.7861 x, 2352.46 - 1.24075 x, 2326.56 - 1.23348 x...}

Graphic representation of data and lines according to the list of equations

After getting the equations, we can display on the chart all points we have and the corresponding equations.
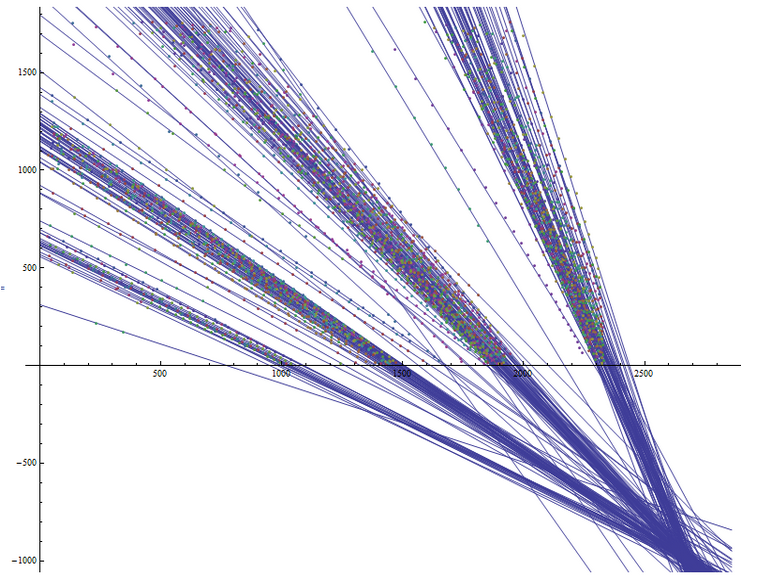
To display a list of points on the graph in Mathematica, there is a ListPlot[] function, and to display functions, there is a Plot[] function. In order to display a graph with points and function graphs on one graph, or to override graph parameters, there is a Show[] function. Let's write these functions for our case:

eqlineplot = Plot[numeq[[Range[length]]], {x, 0, Xlen}];
numplot = ListPlot[num[[Range[length]]]];
Show[
eqlineplot,
numplot,
AspectRatio -> 3/4, Frame -> False,
PlotRange -> {{0, Xlen}, {0, Ylen}}]

And the result of its implementation:



This graph is reversible relative to the axis OX, since his point of origin is in the lower left edge, and not like the camera - in the upper left. But this does not prevent us from understanding that the lines intersect somewhere in the vicinity of a single point - a point from which we will continue to measure angles. Below is a graph with slightly modified drawing areas, which shows the intersection of lines in the vicinity of one point:



Let's take a closer look at the function entries:

eqlineplot = Plot [numeq [[Range [length]]], {x, 0, Xlen}];

Plot [list of features that appear on the graph,
{variable whose functions are built,
its minimum value
its maximum value}]

Range [imax] - generates a list of numeric elements {1, 2, ..., imax}

Show [
eqlineplot
numplot
AspectRatio -> 3/4, Frame -> False,
PlotRange -> {{0, Xlen}, {0, Ylen}}]

AspectRatio -> 3/4 - Set Aspect Ratios
PlotRange -> {{0, Xlen}, {0, Ylen}} set the range of drawing graphs in the X and Y coordinates
Frame -> False - we inform Mathematica that around the graph it is not necessary to draw a frame.

What's next?

In the sequel, if you find it interesting and necessary, I will talk about several techniques for finding the points of intersection of graphs, introduce you to statistical data processing and data analysis using the example of the problem in question.