Graphic Password Vulnerability
Background: my wife constantly strives to somehow screw me up: set the alarm clock at 3 am, change the ringtone, take down the synchronization settings, delete my SMS and then prove that she did not say that.
Joking as a joke, but at some point I decided: “Enough!” - and put the graphic password on my android.
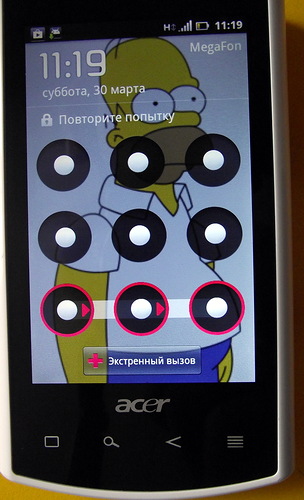
Wife grinned and said she would pick up. I laughed in response, on that and went their separate ways. Only now she was worried about how to choose, and what was the probability of this event?
The very first and logical thought to come up with a mathematical way to calculate combinations.
You need to set the initial conditions:
')
Attempts to figure out the options mathematically were unsuccessful. The conditions imposed did not allow to reveal the rules.
Next step: bust. Not that I was hoping to go through all the tens of thousands of options. The main idea was to find patterns.
I spent a few hours drawing diagrams. But all the laws rested on the symmetry and the fact that all the corner points are equivalent, like all intermediate (except the central).
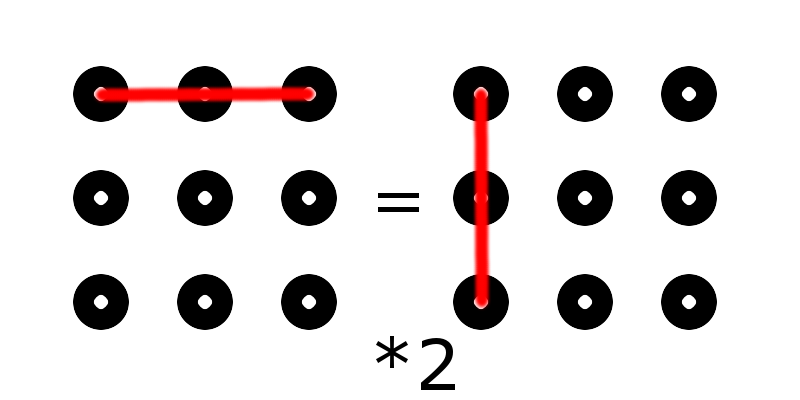

But when did the difficulties frighten us?
I started all the same with one hop.

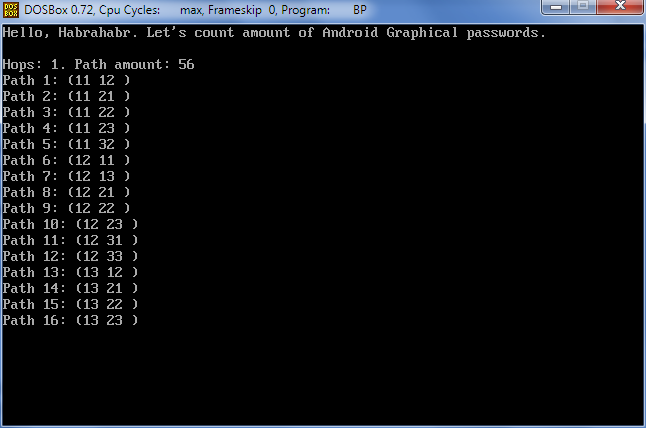
1 hop is easier than steamed turnip - 56 options,
2 hop - nothing complicated - 320 options
3 hop - had to work - 1624 options
4 hop - it was, ahem, tedious - 7152 options
5 hops - mom mia and torn hair - the result is unknown.
Then I decided not to force my brain and remember the long-forgotten programming.
He uncovered the turbopascals, shook the dust off the variables and began to develop an algorithm.
After 4 years of pause and unpretentious scripts on the bash, it took me a whole evening to debug the program. For nothing that the algorithm was born in 20 minutes.
. , 1 4 , 8 — , .

64 . Byte . , 4 :
UPD. .
.
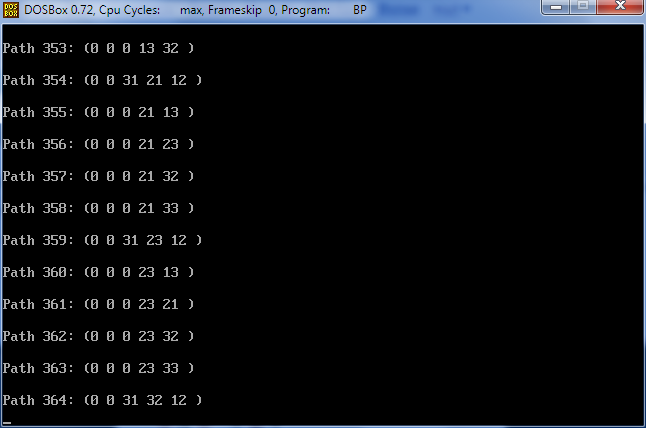
11-22-31-32-12:
:
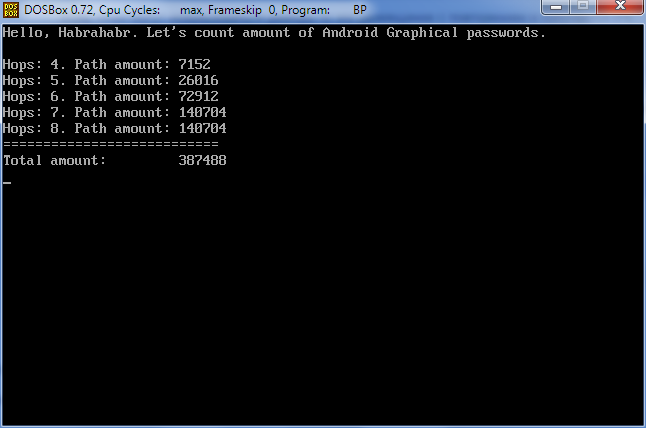
, 389488 .
50% , , , (, ), 194744
20 , .
, 20/194744=,0001. , 0,01%. !
“-” — , . “-” — , .

Joking as a joke, but at some point I decided: “Enough!” - and put the graphic password on my android.

Wife grinned and said she would pick up. I laughed in response, on that and went their separate ways. Only now she was worried about how to choose, and what was the probability of this event?
The very first and logical thought to come up with a mathematical way to calculate combinations.
You need to set the initial conditions:
')
- Direction matters
- Each point can be passed only once.
- To connect the two points they must be in direct view. That is, the first can be connected with the second finger, but not the third.
- The number of points: from 5 to 9. We call one stroke, one connection - hop. That is, we can have from 4 to 8 hop.
Attempts to figure out the options mathematically were unsuccessful. The conditions imposed did not allow to reveal the rules.
Next step: bust. Not that I was hoping to go through all the tens of thousands of options. The main idea was to find patterns.
I spent a few hours drawing diagrams. But all the laws rested on the symmetry and the fact that all the corner points are equivalent, like all intermediate (except the central).


But when did the difficulties frighten us?
I started all the same with one hop.

1 hop is easier than steamed turnip - 56 options,
2 hop - nothing complicated - 320 options
3 hop - had to work - 1624 options
4 hop - it was, ahem, tedious - 7152 options
5 hops - mom mia and torn hair - the result is unknown.
Then I decided not to force my brain and remember the long-forgotten programming.
He uncovered the turbopascals, shook the dust off the variables and began to develop an algorithm.
After 4 years of pause and unpretentious scripts on the bash, it took me a whole evening to debug the program. For nothing that the algorithm was born in 20 minutes.

Code itself
Program First;
Uses Crt;
VAR
i,j,k,cur_i,cur_j,hop_count:byte;
A:array[1..3,1..3] of byte;
Bom:Array[1..10000,1..5] of byte;
path_num,total,m,n:longint;
Procedure PATH(cur_i,cur_j:byte; k:byte);
VAR
i,j:byte;
m,n:integer;
begin
{We will calclate only path amount, but not detailed paths, because of
limitation to array size.
Actually you can make detailed path up to 5 hops. You just should uncomment
calculating of array 'Bom'}
A[cur_i,cur_j]:=1;
for i:=1 to 3 do
begin
for j:=1 to 3 do
begin
{ Bom[path_num,k]:=cur_i*10+cur_j;}
if k<hop_count then
begin
{Checking possibility of doing next-hop}
if (A[i,j]=0)and
not(
((i=cur_i)and(abs(j-cur_j)>1)and(A[i,2]=0))
or
((j=cur_j)and(abs(i-cur_i)>1)and(A[2,j]=0))
or
( (abs(i-cur_i)>1) and (abs(j-cur_j)>1) and (A[2,2]=0))
)
then
begin
{We will enlarge path number if hop amount in path is
qual to actual hop amount only}
if k=hop_count then
begin
path_num:=path_num+1;
{ Bom[path_num,k+1]:=i*10+j;}
end;
A[i,j]:=1;
{Recursive running of path calculation}
PATH(i,j,k+1);
A[i,j]:=0;
end;
end
else
begin
if (A[i,j]=0)and
not(
((i=cur_i)and(abs(j-cur_j)>1)and(A[i,2]=0))
or
((j=cur_j)and(abs(i-cur_i)>1)and(A[2,j]=0))
or
( (abs(i-cur_i)>1) and (abs(j-cur_j)>1) and (A[2,2]=0))
)
then
begin
{Enlarge path number after exit out of procedure}
{ Bom[path_num,k+1]:=i*10+j;}
path_num:=path_num+1;
end;
end;
end;
end;
end;
begin
{A[x,y] - Array of 0 and 1.
0 - this point isn't in path yet. You can move here.
1 - this point is in path already. You can't move here.
}
ClrScr;
writeln ('Hello, Habrahabr. Let','''','s count amount of Android Graphical passwords.');
writeln;
i:=1;
j:=1;
k:=1;
for hop_count:=4 to 8 do
begin
path_num:=1;
for i:=1 to 3 do
for j:=1 to 3 do
begin
{ Bom[path_num,k]:=10*i+j;}
PATH(i,j,k);
a[i,j]:=0;
end;
writeln('Hops: ',hop_count,'. Path amount: ',path_num-1);
total:=total+path_num-1;
end;
writeln('===========================');
writeln('Total amount: ',total);
{Output of full list of paths.}
{for m:=1 to path_num do
begin
write('Path ', m,': (');
for n:=1 to hop_count+1 do
begin
write(Bom[m,n],' ');
end;
writeln(')');
readln;
end;{}
readln;
end.
. , 1 4 , 8 — , .

64 . Byte . , 4 :

UPD. .
.
11-22-31-32-12:

:

, 389488 .
50% , , , (, ), 194744

20 , .
, 20/194744=,0001. , 0,01%. !
“-” — , . “-” — , .

Source: https://habr.com/ru/post/174773/
All Articles